Vad är superposition inom kvantberäkning?
Om katten från föregående enhet var en kvantkatt skulle kvantkattens tillstånd och lådsystemet vara detsamma: summan av kvantkattens sex olika positioner med avseende på lådan, viktad av sannolikheten att hitta kvantkatten i den positionen. Den enda skillnaden är att den klassiska katten kan vara i en (och bara en) av sex möjliga positioner medan kvantkatten kan vara i alla sex positioner samtidigt!
I den klassiska världen kan objekt bara vara i ett tillstånd i taget. Men i kvantvärlden kan kvantpartiklar finnas i flera tillstånd samtidigt. Detta fenomen kallas superposition.
Inom kvantberäkning använder ingen kvantkatter – tyvärr – utan kvantbitar. Ordet "qubit" betyder "kvantbit". Precis som i klassisk databehandling, där den grundläggande informationsenheten är biten, är den grundläggande informationsenheten kvantbiten i kvantberäkning. Och precis som biten kan ta två möjliga värden, 0 och 1, är en kvantbit alla kvantpartiklar som kan vara i två möjliga tillstånd. En qubit kan till exempel vara en foton, som kan polariseras i två riktningar, eller en elektron, som kan vara i två energinivåer.
Hur kan du representera superpositionen i en qubit? Vad är sannolikheten för att hitta en kvantbit i ett visst tillstånd?
Hur kan du representera superpositionen i en qubit?
En kvantbit är en kvantpartikel som har två möjliga positioner eller tillstånd. Som analogt med den klassiska biten kallas kvanttillstånden för en kvantbit också $0$ och $1$. En qubit kan vara i tillståndet $0$, i tillståndet $1$, och i alla superpositioner i båda delstaterna. Hur kan du representera den här superpositionen?
Tänk dig att du ritar en cirkel och en lodrät och vågrät axel så att mittpunkten är mitten av cirkeln. Tillståndet $0$ placeras på den övre punkten på den lodräta axeln och tillståndet $1$ ligger på den nedre punkten.
Hur kan du beskriva den här representationen? Du kan säga att tillståndet $0$ är en pil, eller en vektor, som pekar uppåt och tillståndet $1$ är en vektor som pekar nedåt. Därför skulle en klassisk bit vara en vektor som pekar antingen uppåt eller nedåt, men aldrig i någon annan riktning.
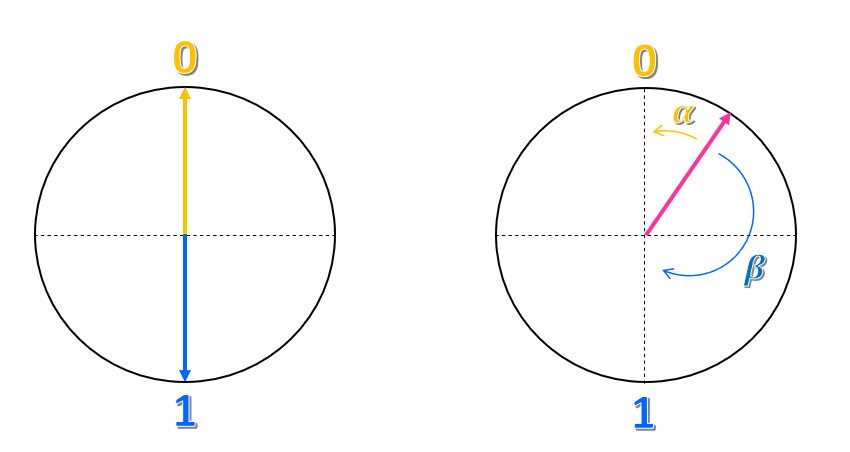
Hur är det med någon annan punkt i cirkeln? Hur kan du representera det tillståndet? Precis som koordinaterna i ett plan kan du försöka representera det som en kombination av de två delstaterna $0$ och $1$. Du kan till exempel ta hur nära vektorn är från tillståndet $0$ och anropa den här vinkeln $\alpha$, och hur nära är från tillståndet $1$ och anropa den här vinkeln $\beta$. Vi kan representera tillståndet som $\alpha 0 + \beta 1 $. Därför är tillståndet en superposition av delstaterna $0$ och $1$.
Precis som exemplet med katten och rutan är det globala tillståndet för en qubit summan av de enskilda tillstånden, $0$ och $1$, viktade med sannolikheten att hitta kvantbiten i det tillståndet, $\alpha$ och $\beta $.
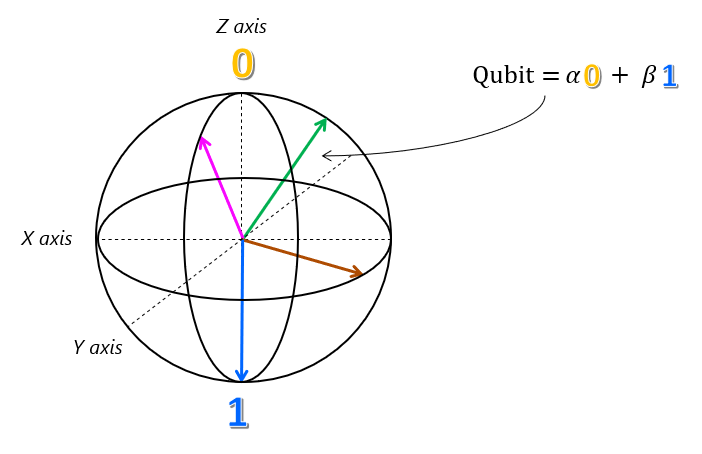
Den här representationen av en qubit är faktiskt korrekt, och den kallas Bloch-sfären.
Dricks
Bloch-sfären är ett kraftfullt verktyg eftersom de åtgärder som vi kan utföra på en qubit kan representeras som rotationer om en av kardinalaxlarna. Även om det är en kraftfull intuition att tänka på en kvantberäkning som en sekvens av rotationer, är det svårt att använda denna intuition för att utforma och beskriva algoritmer. Q# lindrar det här problemet genom att tillhandahålla ett språk för att beskriva sådana rotationer.
Vad är sannolikheten för att hitta en kvantbit i ett tillstånd?
Precis som i exemplet med katten och rutan i föregående enhet är det globala tillståndet för en qubit summan av de enskilda tillstånden, $0$ och $1$, viktade med sannolikheten att hitta kvantbiten i det tillståndet, $\alpha$ och $\beta $. Siffrorna $\alpha$ och $\beta$ representerar hur "stäng" qubittillståndet är för delstaterna $0$ respektive $1$. Är $\alpha$ och $\beta$ sannolikheten att hitta kvantbiten i tillståndet $0$ eller $1$? Inte exakt.
Siffrorna $\alpha$ och $\beta$ är sannolikhetsamplituder för varje tillstånd. Deras absoluta värden, till exempel $|\alpha|^2$ ger motsvarande sannolikheter. Sannolikheten för att observera tillståndet $0$ är till exempel $|\alpha|^2$, och sannolikheten för att observera tillståndet $1$ är $|\beta|^2$.
Siffrorna $\alpha$ och $\beta$ kan vara positiva, negativa eller till och med komplexa tal. I en giltig kvantsuperposition måste dock alla sannolikheter summeras till en: $|\alpha|^2+|\beta|^2=1$. Den här begränsningen kallas för normaliseringsvillkoret. Du kan tänka på normaliseringsvillkoret som det faktum att du alltid får ett resultat när du mäter, så sannolikheten för att mäta varje tänkbart resultat måste summeras till en.