Övning – Beräkna resurser för ett verkligt problem
Shors factoringalgoritm är en av de mest kända kvantalgoritmerna. Den erbjuder en exponentiell hastighet över alla kända klassiska factoringalgoritmer.
Klassisk kryptografi använder fysiska eller matematiska medel, till exempel beräkningssvårigheter, för att utföra en uppgift. Ett populärt kryptografiskt protokoll är systemet Rivest–Shamir–Adleman (RSA), som baseras på antagandet att det är svårt att räkna ut primtal med hjälp av en klassisk dator.
Shor-algoritmen innebär att tillräckligt stora kvantdatorer kan bryta kryptografi med offentliga nycklar. Det är viktigt att uppskatta de resurser som krävs för Shor-algoritmen för att bedöma sårbarheten för dessa typer av kryptografiska scheman.
I följande övning beräknar du resursberäkningar för factoring av ett 2 048-bitars heltal. För det här programmet beräknar du de fysiska resursuppskattningarna direkt från förberäknade logiska resursuppskattningar. För den tolererade felbudgeten använder du $\epsilon = 1/3$.
Skriva Shor-algoritmen
I Visual Studio Code väljer du Visa > kommandopalett och väljer Skapa: Ny Jupyter Notebook.
Spara notebook-filen som ShorRE.ipynb.
Importera paketet i den första cellen
qsharp:import qsharpMicrosoft.Quantum.ResourceEstimationAnvänd namnområdet för att definiera en cachelagrad, optimerad version av Shors heltalsfaktoriseringsalgoritm. Lägg till en ny cell och kopiera och klistra in följande kod:%%qsharp open Microsoft.Quantum.Arrays; open Microsoft.Quantum.Canon; open Microsoft.Quantum.Convert; open Microsoft.Quantum.Diagnostics; open Microsoft.Quantum.Intrinsic; open Microsoft.Quantum.Math; open Microsoft.Quantum.Measurement; open Microsoft.Quantum.Unstable.Arithmetic; open Microsoft.Quantum.ResourceEstimation; operation RunProgram() : Unit { let bitsize = 31; // When choosing parameters for `EstimateFrequency`, make sure that // generator and modules are not co-prime let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize); } // In this sample we concentrate on costing the `EstimateFrequency` // operation, which is the core quantum operation in Shors algorithm, and // we omit the classical pre- and post-processing. /// # Summary /// Estimates the frequency of a generator /// in the residue ring Z mod `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order (period) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## bitsize /// Number of bits needed to represent the modulus. /// /// # Output /// The numerator k of dyadic fraction k/2^bitsPrecision /// approximating s/r. operation EstimateFrequency( generator : Int, modulus : Int, bitsize : Int ) : Int { mutable frequencyEstimate = 0; let bitsPrecision = 2 * bitsize + 1; // Allocate qubits for the superposition of eigenstates of // the oracle that is used in period finding. use eigenstateRegister = Qubit[bitsize]; // Initialize eigenstateRegister to 1, which is a superposition of // the eigenstates we are estimating the phases of. // We first interpret the register as encoding an unsigned integer // in little endian encoding. ApplyXorInPlace(1, eigenstateRegister); let oracle = ApplyOrderFindingOracle(generator, modulus, _, _); // Use phase estimation with a semiclassical Fourier transform to // estimate the frequency. use c = Qubit(); for idx in bitsPrecision - 1..-1..0 { within { H(c); } apply { // `BeginEstimateCaching` and `EndEstimateCaching` are the operations // exposed by Azure Quantum Resource Estimator. These will instruct // resource counting such that the if-block will be executed // only once, its resources will be cached, and appended in // every other iteration. if BeginEstimateCaching("ControlledOracle", SingleVariant()) { Controlled oracle([c], (1 <<< idx, eigenstateRegister)); EndEstimateCaching(); } R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c); } if MResetZ(c) == One { set frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx); } } // Return all the qubits used for oracles eigenstate back to 0 state // using Microsoft.Quantum.Intrinsic.ResetAll. ResetAll(eigenstateRegister); return frequencyEstimate; } /// # Summary /// Interprets `target` as encoding unsigned little-endian integer k /// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where /// p is `power`, g is `generator` and N is `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order ( period ) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## power /// Power of `generator` by which `target` is multiplied. /// ## target /// Register interpreted as LittleEndian which is multiplied by /// given power of the generator. The multiplication is performed modulo /// `modulus`. internal operation ApplyOrderFindingOracle( generator : Int, modulus : Int, power : Int, target : Qubit[] ) : Unit is Adj + Ctl { // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We // also use `ExpModI` to compute a by which x must be multiplied. Also // note that we interpret target as unsigned integer in little-endian // encoding by using the `LittleEndian` type. ModularMultiplyByConstant(modulus, ExpModI(generator, power, modulus), target); } /// # Summary /// Performs modular in-place multiplication by a classical constant. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register (as LittleEndian) |𝑦⟩, this operation /// computes `(c*x) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular multiplication /// ## c /// Constant by which to multiply |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { use qs = Qubit[Length(y)]; for (idx, yq) in Enumerated(y) { let shiftedC = (c <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, shiftedC, qs)); } ApplyToEachCA(SWAP, Zipped(y, qs)); let invC = InverseModI(c, modulus); for (idx, yq) in Enumerated(y) { let shiftedC = (invC <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs)); } } /// # Summary /// Performs modular in-place addition of a classical constant into a /// quantum register. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register (as LittleEndian) |𝑦⟩, this operation /// computes `(x+c) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular addition /// ## c /// Constant to add to |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { body (...) { Controlled ModularAddConstant([], (modulus, c, y)); } controlled (ctrls, ...) { // We apply a custom strategy to control this operation instead of // letting the compiler create the controlled variant for us in which // the `Controlled` functor would be distributed over each operation // in the body. // // Here we can use some scratch memory to save ensure that at most one // control qubit is used for costly operations such as `AddConstant` // and `CompareGreaterThenOrEqualConstant`. if Length(ctrls) >= 2 { use control = Qubit(); within { Controlled X(ctrls, control); } apply { Controlled ModularAddConstant([control], (modulus, c, y)); } } else { use carry = Qubit(); Controlled AddConstant(ctrls, (c, y + [carry])); Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry])); Controlled AddConstant([carry], (modulus, y)); Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry)); } } } /// # Summary /// Performs in-place addition of a constant into a quantum register. /// /// # Description /// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive /// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩. /// /// # Input /// ## c /// Constant number to add to |𝑦⟩. /// ## y /// Quantum register of second summand and target; must not be empty. internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl { // We are using this version instead of the library version that is based // on Fourier angles to show an advantage of sparse simulation in this sample. let n = Length(y); Fact(n > 0, "Bit width must be at least 1"); Fact(c >= 0, "constant must not be negative"); Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}"); if c != 0 { // If c has j trailing zeroes than the j least significant bits // of y will not be affected by the addition and can therefore be // ignored by applying the addition only to the other qubits and // shifting c accordingly. let j = NTrailingZeroes(c); use x = Qubit[n - j]; within { ApplyXorInPlace(c >>> j, x); } apply { IncByLE(x, y[j...]); } } } /// # Summary /// Performs greater-than-or-equals comparison to a constant. /// /// # Description /// Toggles output qubit `target` if and only if input register `x` /// is greater than or equal to `c`. /// /// # Input /// ## c /// Constant value for comparison. /// ## x /// Quantum register to compare against. /// ## target /// Target qubit for comparison result. /// /// # Reference /// This construction is described in [Lemma 3, arXiv:2201.10200] internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit) : Unit is Adj+Ctl { let bitWidth = Length(x); if c == 0 { X(target); } elif c >= 2 ^ bitWidth { // do nothing } elif c == 2 ^ (bitWidth - 1) { ApplyLowTCNOT(Tail(x), target); } else { // normalize constant let l = NTrailingZeroes(c); let cNormalized = c >>> l; let xNormalized = x[l...]; let bitWidthNormalized = Length(xNormalized); let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized)); use qs = Qubit[bitWidthNormalized - 1]; let cs1 = [Head(xNormalized)] + Most(qs); let cs2 = Rest(xNormalized); within { for i in IndexRange(gates) { (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]); } } apply { ApplyLowTCNOT(Tail(qs), target); } } } /// # Summary /// Internal operation used in the implementation of GreaterThanOrEqualConstant. internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { within { ApplyToEachA(X, [control1, control2]); } apply { ApplyAnd(control1, control2, target); X(target); } } internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { body (...) { CCNOT(control1, control2, target); } adjoint (...) { H(target); if (M(target) == One) { X(target); CZ(control1, control2); } } } /// # Summary /// Returns the number of trailing zeroes of a number /// /// ## Example /// ```qsharp /// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0 /// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2 /// ``` internal function NTrailingZeroes(number : Int) : Int { mutable nZeroes = 0; mutable copy = number; while (copy % 2 == 0) { set nZeroes += 1; set copy /= 2; } return nZeroes; } /// # Summary /// An implementation for `CNOT` that when controlled using a single control uses /// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7. internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl { body (...) { CNOT(a, b); } adjoint self; controlled (ctls, ...) { // In this application this operation is used in a way that // it is controlled by at most one qubit. Fact(Length(ctls) <= 1, "At most one control line allowed"); if IsEmpty(ctls) { CNOT(a, b); } else { use q = Qubit(); within { ApplyAnd(Head(ctls), a, q); } apply { CNOT(q, b); } } } controlled adjoint self; }
Beräkna Shor-algoritmen
Beräkna nu de fysiska resurserna för RunProgram åtgärden med hjälp av standardantagandena. Lägg till en ny cell och kopiera och klistra in följande kod:
result = qsharp.estimate("RunProgram()")
result
Funktionen qsharp.estimate skapar ett resultatobjekt som du kan använda för att visa en tabell med det totala antalet fysiska resurser. Du kan kontrollera kostnadsinformationen genom att komprimera grupperna, som har mer information.
Dölj till exempel gruppen Logiska qubitparametrar för att se att kodavståndet är 21 och att antalet fysiska kvantbitar är 882.
| Logisk qubit-parameter | Värde |
|---|---|
| QEC-schema | surface_code |
| Kodavstånd | 21 |
| Fysiska kvantbitar | 882 |
| Logisk cykeltid | 8 milisecs |
| Felfrekvens för logisk kvantbit | 3.00E-13 |
| Korsande förfaktor | 0.03 |
| Tröskelvärde för felkorrigering | 0.01 |
| Formel för logisk cykeltid | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Formel för fysiska kvantbitar | 2 * codeDistance * codeDistance |
Dricks
Om du vill ha en mer kompakt version av utdatatabellen kan du använda result.summary.
Blankstegsdiagram
Fördelningen av fysiska kvantbitar som används för algoritmen och T-fabrikerna är en faktor som kan påverka algoritmens design. Du kan använda qsharp-widgets paketet för att visualisera den här distributionen för att bättre förstå algoritmens uppskattade utrymmeskrav.
from qsharp_widgets import SpaceChart
SpaceChart(result)
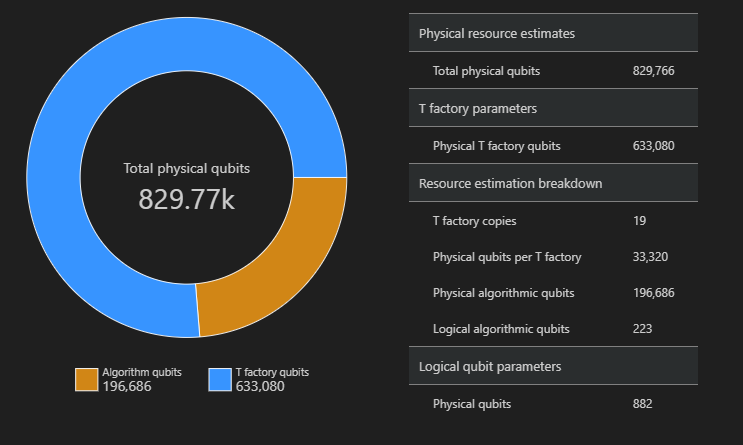
I det här exemplet är antalet fysiska kvantbitar som krävs för att köra algoritmen 829766, varav 196686 är algoritmkvbitar och 633080 som är T-fabriks qubitar.
Jämför resursuppskattningarna för olika kvantbitstekniker
Med Azure Quantum Resource Estimator kan du köra flera konfigurationer av målparametrar och jämföra resultaten. Detta är användbart när du vill jämföra kostnaden för olika qubit-modeller, QEC-scheman eller felbudgetar.
Du kan också skapa en lista med uppskattningsparametrar med hjälp av EstimatorParams objektet.
from qsharp.estimator import EstimatorParams, QubitParams, QECScheme, LogicalCounts
labels = ["Gate-based µs, 10⁻³", "Gate-based µs, 10⁻⁴", "Gate-based ns, 10⁻³", "Gate-based ns, 10⁻⁴", "Majorana ns, 10⁻⁴", "Majorana ns, 10⁻⁶"]
params = EstimatorParams(6)
params.error_budget = 0.333
params.items[0].qubit_params.name = QubitParams.GATE_US_E3
params.items[1].qubit_params.name = QubitParams.GATE_US_E4
params.items[2].qubit_params.name = QubitParams.GATE_NS_E3
params.items[3].qubit_params.name = QubitParams.GATE_NS_E4
params.items[4].qubit_params.name = QubitParams.MAJ_NS_E4
params.items[4].qec_scheme.name = QECScheme.FLOQUET_CODE
params.items[5].qubit_params.name = QubitParams.MAJ_NS_E6
params.items[5].qec_scheme.name = QECScheme.FLOQUET_CODE
qsharp.estimate("RunProgram()", params=params).summary_data_frame(labels=labels)
| Qubit-modell | Logiska kvantbitar | Logiskt djup | T-tillstånd | Kodavstånd | T-fabriker | T-fabriksfraktion | Fysiska kvantbitar | rQOPS | Fysisk körning |
|---|---|---|---|---|---|---|---|---|---|
| Grindbaserade μs, 10⁻³ | 223 3,64 M | 4,70 M | 17 | 13 | 40.54 % | 216.77k | 21.86k | 10 timmar | |
| Grindbaserade μs, 10⁻⁴ | 223 | 3,64 M | 4,70 M | 9 | 14 | 43.17 % | 63.57k | 41.30k | 5 timmar |
| Grindbaserade ns, 10⁻³ | 223 3,64 M | 4,70 M | 17 | 16 | 69.08 % | 416.89k | 32,79 M | 25 sekunder | |
| Gate-baserade ns, 10⁻⁴ | 223 3,64 M | 4,70 M | 9 | 14 | 43.17 % | 63.57k | 61,94 M | 13 sekunder | |
| Majorana ns, 10⁻⁴ | 223 3,64 M | 4,70 M | 9 | 19 | 82.75 % | 501.48k | 82.59M | 10 sekunder | |
| Majorana ns, 10⁻⁶ | 223 3,64 M | 4,70 M | 5 | 13 | 31.47 % | 42.96k | 148,67 M | 5 sekunder |
Extrahera resursuppskattningar från antalet logiska resurser
Om du redan känner till några uppskattningar för en åtgärd kan du använda Resource Estimator för att införliva kända uppskattningar i den totala programkostnaden för att minska körningstiden. Du kan använda LogicalCounts klassen för att extrahera de logiska resursuppskattningarna från förberäknade resursuppskattningsvärden.
Välj Kod för att lägga till en ny cell och ange och kör sedan följande kod:
logical_counts = LogicalCounts({
'numQubits': 12581,
'tCount': 12,
'rotationCount': 12,
'rotationDepth': 12,
'cczCount': 3731607428,
'measurementCount': 1078154040})
logical_counts.estimate(params).summary_data_frame(labels=labels)
| Qubit-modell | Logiska kvantbitar | Logiskt djup | T-tillstånd | Kodavstånd | T-fabriker | T-fabriksfraktion | Fysiska kvantbitar | Fysisk körning |
|---|---|---|---|---|---|---|---|---|
| Grindbaserade μs, 10⁻³ | 25481 | 1.2e+10 | 1.5e+10 | 27 | 13 | 0,6 % | 37,38 M | 6 år |
| Grindbaserade μs, 10⁻⁴ | 25481 | 1.2e+10 | 1.5e+10 | 13 | 14 | 0,8 % | 8,68 M | 3 år |
| Grindbaserade ns, 10⁻³ | 25481 | 1.2e+10 | 1.5e+10 | 27 | 15 | 1,3 % | 37,65 M | 2 dagar |
| Gate-baserade ns, 10⁻⁴ | 25481 | 1.2e+10 | 1.5e+10 | 13 | 18 | 1,2 % | 8,72 M | 18 timmar |
| Majorana ns, 10⁻⁴ | 25481 | 1.2e+10 | 1.5e+10 | 15 | 15 | 1,3 % | 26.11M | 15 timmar |
| Majorana ns, 10⁻⁶ | 25481 | 1.2e+10 | 1.5e+10 | 7 | 13 | 0,5 % | 6,25 M | 7 timmar |
Slutsats
I det värsta scenariot skulle en kvantdator som använder gatebaserade μs-kvantbitar (kvantbitar som har driftstider i nanosekundersregimen, till exempel supraledande kvantbitar) och en QEC-kod på ytan behöva sex år och 37,38 miljoner kvantbitar för att räkna in ett 2 048-bitars heltal med hjälp av Shors algoritm.
Om du använder en annan qubit-teknik, till exempel gate-baserade ns-jon-kvantbitar, och samma ytkod, ändras inte antalet kvantbitar mycket, men körningen blir två dagar i värsta fall och 18 timmar i optimistiskt fall. Om du ändrar kvantbitstekniken och QEC-koden, till exempel med hjälp av Majorana-baserade kvantbitar, kan det gå att beräkna ett 2 048-bitars heltal med hjälp av Shor-algoritmen på flera timmar med en matris med 6,25 miljoner kvantbitar i bästa fall.
Från experimentet kan du dra slutsatsen att använda Majorana-kvantbitar och en Floquet QEC-kod är det bästa valet för att köra Shor-algoritmen och ta med ett 2 048-bitars heltal.