Redigera

Dela via

Polygon

  • Artikel

Applies to: SQL Server Azure SQL Database Azure SQL Managed Instance SQL analytics endpoint in Microsoft Fabric Warehouse in Microsoft Fabric SQL database in Microsoft Fabric

A Polygon is a two-dimensional surface stored as a sequence of points defining an exterior bounding ring and zero or more interior rings.

Polygon instances

A Polygon instance can be formed from a ring that has at least three distinct points. A Polygon instance can also be empty.

The exterior and any interior rings of a Polygon define its boundary. The space within the rings defines the interior of the Polygon.

The following illustration shows examples of Polygon instances.

Examples of geometry Polygon instances.

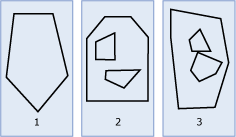
As shown in the illustration:

  1. Figure 1 is a Polygon instance whose boundary is defined by an exterior ring.

  2. Figure 2 is a Polygon instance whose boundary is defined by an exterior ring and two interior rings. The area inside the interior rings is part of the exterior of the Polygon instance.

  3. Figure 3 is a valid Polygon instance because its interior rings intersect at a single tangent point.

Accepted instances

Accepted Polygon instances are instances that can be stored in a geometry or geography variable without throwing an exception. The following are accepted Polygon instances:

  • An Empty Polygon instance
  • A Polygon instance that has an acceptable exterior ring (LineString) and zero or more acceptable interior rings (LineStrings)

The following criteria are needed for a ring (LineString) to be acceptable.

  • The LineString instance must be accepted.
  • The LineString instance must have at least four points.
  • The starting and ending points of the LineString instance must be the same.

The following example shows accepted Polygon instances.

DECLARE @g1 geometry = 'POLYGON EMPTY';  
DECLARE @g2 geometry = 'POLYGON((1 1, 3 3, 3 1, 1 1))';  
DECLARE @g3 geometry = 'POLYGON((-5 -5, -5 5, 5 5, 5 -5, -5 -5),(0 0, 3 0, 3 3, 0 3, 0 0))';  
DECLARE @g4 geometry = 'POLYGON((-5 -5, -5 5, 5 5, 5 -5, -5 -5),(3 0, 6 0, 6 3, 3 3, 3 0))';  
DECLARE @g5 geometry = 'POLYGON((1 1, 1 1, 1 1, 1 1))';

As @g4 and @g5 show an accepted Polygon instance might not be a valid Polygon instance. @g5 also shows that a Polygon instance needs to only contain a ring with any four points to be accepted.

The following examples throw a System.FormatException because the Polygon instances aren't accepted.

DECLARE @g1 geometry = 'POLYGON((1 1, 3 3, 1 1))';  
DECLARE @g2 geometry = 'POLYGON((1 1, 3 3, 3 1, 1 5))';

@g1 isn't accepted because the LineString instance for the exterior ring doesn't contain enough points. @g2 isn't accepted because the starting point of the exterior ring LineString instance isn't the same as the ending point. The following example has an acceptable exterior ring, but the interior ring isn't acceptable. This also throws a System.FormatException.

DECLARE @g geometry = 'POLYGON((-5 -5, -5 5, 5 5, 5 -5, -5 -5),(0 0, 3 0, 0 0))';

Valid instances

The interior rings of a Polygon can touch both themselves and each other at single tangent points, but if the interior rings of a Polygon cross, the instance isn't valid.

The following example shows valid Polygon instances.

DECLARE @g1 geometry = 'POLYGON((-20 -20, -20 20, 20 20, 20 -20, -20 -20))';  
DECLARE @g2 geometry = 'POLYGON((-20 -20, -20 20, 20 20, 20 -20, -20 -20), (10 0, 0 10, 0 -10, 10 0))';  
DECLARE @g3 geometry = 'POLYGON((-20 -20, -20 20, 20 20, 20 -20, -20 -20), (10 0, 0 10, 0 -10, 10 0), (-10 0, 0 10, -5 -10, -10 0))';  
SELECT @g1.STIsValid(), @g2.STIsValid(), @g3.STIsValid();

@g3 is valid because the two interior rings touch at a single point and do not cross each other. The following example shows Polygon instances that aren't valid.

DECLARE @g1 geometry = 'POLYGON((-20 -20, -20 20, 20 20, 20 -20, -20 -20), (20 0, 0 10, 0 -20, 20 0))';  
DECLARE @g2 geometry = 'POLYGON((-20 -20, -20 20, 20 20, 20 -20, -20 -20), (10 0, 0 10, 0 -10, 10 0), (5 0, 1 5, 1 -5, 5 0))';  
DECLARE @g3 geometry = 'POLYGON((-20 -20, -20 20, 20 20, 20 -20, -20 -20), (10 0, 0 10, 0 -10, 10 0), (-10 0, 0 10, 0 -10, -10 0))';  
DECLARE @g4 geometry = 'POLYGON((-20 -20, -20 20, 20 20, 20 -20, -20 -20), (10 0, 0 10, 0 -10, 10 0), (-10 0, 1 5, 0 -10, -10 0))';  
DECLARE @g5 geometry = 'POLYGON((10 0, 0 10, 0 -10, 10 0), (-20 -20, -20 20, 20 20, 20 -20, -20 -20) )';  
DECLARE @g6 geometry = 'POLYGON((1 1, 1 1, 1 1, 1 1))';  
SELECT @g1.STIsValid(), @g2.STIsValid(), @g3.STIsValid(), @g4.STIsValid(), @g5.STIsValid(), @g6.STIsValid();

@g1 isn't valid because the inner ring touches the exterior ring in two places. @g2 isn't valid because the second inner ring in within the interior of the first inner ring. @g3 isn't valid because the two inner rings touch at multiple consecutive points. @g4 isn't valid because the interiors of the two inner rings overlap. @g5 isn't valid because the exterior ring isn't the first ring. @g6 isn't valid because the ring doesn't have at least three distinct points.

Orientation of spatial data

The ring orientation of a polygon isn't an important factor in the planar system. The OGC Simple Features for SQL Specification doesn't dictate a ring ordering, and SQL Server doesn't enforce ring ordering.

In an ellipsoidal system, a polygon without an orientation has no meaning, or is ambiguous. For example, does a ring around the equator describe the northern or southern hemisphere? If we use the geography data type to store the spatial instance, we must specify the orientation of the ring and accurately describe the location of the instance.

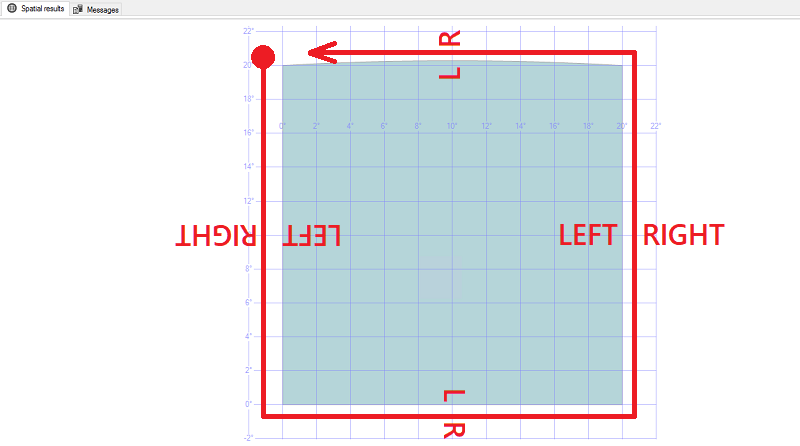
The interior of the polygon in an ellipsoidal system is defined by the "left-hand rule": if you imagine yourself walking along the ring of a geography Polygon, following the points in the order in which they are listed, the area on the left is being treated as the interior of the Polygon, and the area on the right as the exterior of the Polygon.

Counter-clockwise

DECLARE @square GEOGRAPHY;
SET @square = GEOGRAPHY::STPolyFromText('POLYGON((0 20, 0 0, 20 0, 20 20, 0 20))', 4326);
SELECT @square;

Visualization of 'left-hand rule' counter-clockwise orientation.

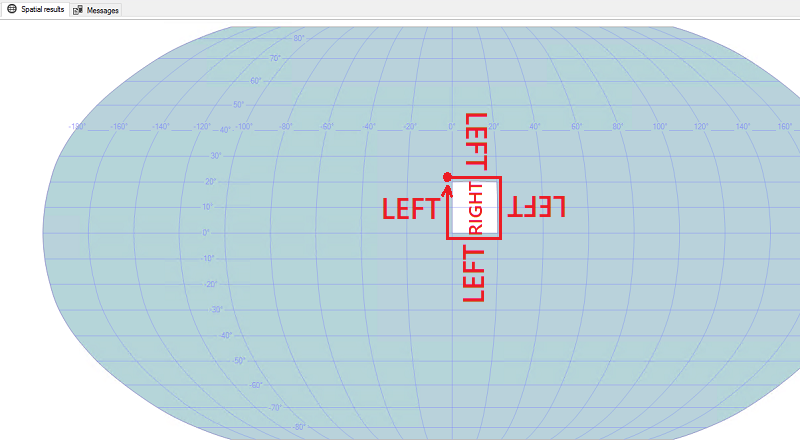
Clockwise

DECLARE @square GEOGRAPHY;
SET @square = GEOGRAPHY::STPolyFromText('POLYGON((0 20, 20 20, 20 0, 0 0, 0 20))', 4326);
SELECT @square;

Visualization of 'left-hand rule' clockwise orientation.

When the compatibility level is 100 or lower in SQL Server, the geography data type has the following restrictions:

  • Each geography instance must fit inside a single hemisphere. No spatial objects larger than a hemisphere can be stored.

  • Any geography instance from an Open Geospatial Consortium (OGC) Well-Known Text (WKT) or Well-Known Binary (WKB) representation that produces an object larger than a hemisphere throws an ArgumentException.

  • The geography data type methods that require the input of two geography instances, (such as STIntersection(), STUnion(), STDifference(), and STSymDifference()), will return null if the results from the methods do not fit inside a single hemisphere. STBuffer() will also return null if the output exceeds a single hemisphere.

Orientation can be reversed leveraging the ReorientObject (geography Data Type) extended method.

Examples

Example A.

The following example creates a simple geometry Polygon instance with a gap and SRID 10.

DECLARE @g geometry;  
SET @g = geometry::STPolyFromText(
    'POLYGON((0 0, 0 3, 3 3, 3 0, 0 0), (1 1, 1 2, 2 1, 1 1))',
    10);

Example B.

An instance that isn't valid can be entered and converted to a valid geometry instance. In the following example of a Polygon, the interior and exterior rings overlap and the instance isn't valid.

DECLARE @g geometry;  
SET @g = geometry::Parse(
    'POLYGON((1 0, 0 1, 1 2, 2 1, 1 0), (2 0, 1 1, 2 2, 3 1, 2 0))'
    );

Example C.

In the following example, the invalid instance is made valid with MakeValid().

SET @g = @g.MakeValid();  
SELECT @g.ToString();

The geometry instance returned from the previous example is a MultiPolygon.

MULTIPOLYGON (((2 0, 3 1, 2 2, 1.5 1.5, 2 1, 1.5 0.5, 2 0)),
              ((1 0, 1.5 0.5, 1 1, 1.5 1.5, 1 2, 0 1, 1 0)))

Example D.

This is another example of converting an invalid instance to a valid geometry instance. In the following example the Polygon instance has been created using three points that are exactly the same:

DECLARE @g geometry  
SET @g = geometry::Parse('POLYGON((1 3, 1 3, 1 3, 1 3))');  
SET @g = @g.MakeValid();  
SELECT @g.ToString()

The geometry instance returned previously is a Point(1 3). If the Polygon given is POLYGON((1 3, 1 5, 1 3, 1 3)) then MakeValid() would return LINESTRING(1 3, 1 5).

Related content