Resultat av maskininlärningsmodeller
Det här ämnet innehåller information om sammanblandningsmatris, klassificeringsproblem och noggrannhet i maskininlärningsmodeller (ML). Syftet är att förbättra din förståelse av noggrannhet i ML-förutsägelseresultat. Målgruppen är ingenjörer, analytiker och chefer som vill få större kunskap och kompetens inom datavetenskap.
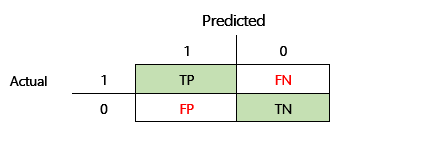
Sammanblandningsmatris
När ett övervakat ML-problem har tränats in på en uppsättning historiska data, testas de med hjälp av data som inte ingår i träningsprocessen. På så sätt kan du jämföra förutsägelserna från den tränade modellen med de faktiska värdena. Med hjälp av sammanblandningsmatrisen kan du utvärdera hur lyckat ett klassificeringsproblem är och var det gör misstag (dvs. var det blir "sammanblandat").
Ditt mål kan till exempel vara att förutsäga om ett husdjur är en hund eller katt, baserat på vissa fysiska och beteendebaserade attribut. Om du har en testdatamängd som innehåller 30 hundar och 20 katter kan sammanblandningsmatrisen likna följande bild.
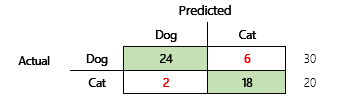
Talen i de gröna cellerna representerar korrekta förutsägelser. Som du ser förutsäger modellen en högre procentandel av faktiska katter på rätt sätt. Modellens övergripande noggrannhet är enkel att beräkna. I det här fallet är den 42 ÷ 50, eller 0,84.
Klassificerare med flera klasser i en sammanblandningsmatris
De flesta diskussioner om sammanblandningsmatrisen är inriktade på binära klassificerare, som i föregående exempel. Det här fallet är ett specialfall där andra mått kan beaktas, till exempel känslighet och återkallning.
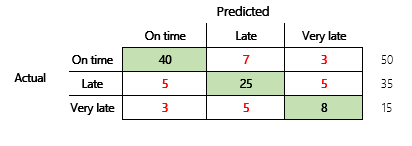
Nu ska vi ta hänsyn till ett klassificeringsproblem för ett finansscenario med tre tillstånd. Modellen förutsäger om en kundfaktura kommer att betalas i tid, sent eller mycket sent. Exempelvis av 100 testfakturor betalas 50 i tid, 35 betalas sent och 15 betalas mycket sent. I det här fallet kan en modell generera en sammanblandningsmatris som liknar bilden nedan.
 ]
]
En sammanblandningsmatris ger betydligt mer information än ett enkelt noggrannhetsmått. Det är dock fortfarande relativt enkelt att förstå. En sammanblandningsmatris visar om du har en balanserad datamängd där utdataklasserna har liknande antal. När det gäller scenariot med flera klasser får du veta hur avvikande en förutsägelse kan vara när utdataklasserna är ordningstal, som i föregående exempel om kundbetalningar.
Modellens noggrannhet
Med olika noggrannhetsmått kan du kvantifiera modellkvaliteten.
Eftersom noggrannhet är ett enkelt mått att förstå, är det en bra utgångspunkt när det gäller att förklara en modell för andra personer, särskilt för användare av modellen som inte är datavetare. Det krävs ingen förståelse för statistik för att förstå modellens noggrannhet. När en sammanblandningsmatris är tillgänglig ger den bättre insikt i modellens prestanda.
För en mer grundlig förståelse bör emellertid flera utmaningar som är förknippade med noggrannhet noteras. Måttets användbarhet beror på problemets kontext. En fråga som ofta uppstår i relation till modellprestanda är, "Hur bra är modellen? Svaret på den här frågan behöver dock inte vara enkelt. Tänk på följande sammanblandningsmatris (modell 2).
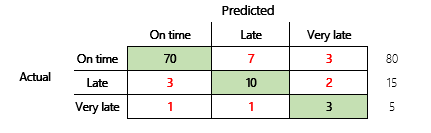
En snabb beräkning visar att den här modellens noggrannhet är (70 + 10 + 3) ÷ 100, eller 0,83. På ytan verkar detta resultat bättre än resultatet för den tidigare modellen med flera klasser (modell 1), vilket har en exakthet på 0,73. Men är det bättre?
För att börja besvara den här frågan bör du beakta hur korrekt en naiv gissning är. För ett klassificeringsproblem kommer en enkel gissning alltid att förutsäga den vanligaste klassen. För modell 1 är gissningen "i tid" och det ger en exakthet på 0,50. Gissningen för modell 2 är också "i tid" och det ger en exakthet på 0,80. Eftersom modell 1 förbättrar den naiva gissningen med 0,73-0,50 = 0,23, och modell 2 förbättrar den naiva gissningen med 0,83-0,80 = 0,03, är modell 1 en bättre modell, även om den har lägre noggrannhet. Beräkningen visar att en effektiv bedömning av en modells kvalitet kräver mer sammanhang än noggrannhetsvärdet.
En annan aspekt är värt att notera. Beakta ett scenario där ett medicinskt test används för att upptäcka en sjukdom i en patient. Det här problemet är ett problem med binära klassificeringar där ett positivt resultat anger att patienten har sjukdomen. I det här scenariot måste du tänka på konsekvenserna av följande fel:
- Falska positiva, där testet anger att en patient har sjukdomen, men patienten inte har sjukdomen.
- Falska negativa, där testet anger att en patient inte har sjukdomen, men patienten har sjukdomen.
Det är uppenbart att båda typerna av fel är oönskade, men vilket fel är värst? Det beror på. När det gäller en livshotande sjukdom som kräver snabb behandling, är minimering falska negativa (förhoppningsvis följda av ytterligare tester) en högre prioritet. I andra mindre kritiska situationer kan den som skapar modellen minimera falska positiva i stället. Oavsett är det en rimlig slutsats att för att effektivt fastställa modellens kvalitet måste du ha mer information än ett noggrannhetsmått.
Rekommendationer
Noggrannhet är ett viktigt verktyg för att kommunicera med domänexperter som inte är bekanta med statistik. För att informationen ska vara användbar är det dock viktigt att den ytterligare kontexten anges tillsammans med noggrannhetsvärdet.
För betalningsförutsägelsescenariot kan du ange ett mål för ML-modellen som inkluderar faktorer i olika betalningsbeteenden. Målet är att modellen ska vara bättre än en naiv gissning genom att antalet felaktiga svar minskas med minst 50 procent. Med andra ord vill du ha en målnoggrannhet som delar upp differensen mellan noggrannheten i en naiv gissning och 100 procent.
I följande tabell sammanfattas den här principen för sammanblandningsmatriserna i det här ämnet.
| Modell | Naiv gissning | Mål | Modellens noggrannhet | Är målet uppfyllt? |
|---|---|---|---|---|
| Modell 1 | 0.50 | 0.75 | 0.73 | Nästan. Den här modellen förbättrar den gissningen betydligt. |
| Modell 2 | 0.80 | 0.90 | 0.83 | Nr Förbättring krävs. |
Klassificering av F1-noggrannhet
Det slutliga övervägandet i det här ämnet är ett mer avancerat mått på klassificerings av ML-prestanda som kallas F1-noggrannhet.
Innan F1-noggrannhet kan definieras måste ytterligare två mått införas: precision och återkallande. Precision anger hur många av det totala antalet förutsägelser som har angetts som positiva som är korrekt tilldelade. Det här måttet kallas även det positiva predikativa värdet. Återkallande är det totala antalet faktiska positiva fall som har förutsagts korrekt. Det här måttet kallas också för känslighet.
I sammanblandningsmatrisen i föregående bild beräknas dessa mått på följande sätt:
- Precision = TP ÷ (TP + FP)
- Återkallande = TP ÷ (TP + FN)
Med F1-måttet kombineras precision och återkallande. Resultatet blir det harmoniska medelvärdet av de två värdena. Det beräknas på följande sätt:
- F1 = 2 × (precision x återkallande) ÷ (precision + återkallande)
Nu ska vi titta på ett konkret exempel. Tidigare i den här artikeln fanns ett exempel på en modell som var förutsade om ett djur är en hund eller katt. Bilden upprepas här.
Här är resultaten om "hund" används som positivt svar.
- Precision = 24 ÷ (24 + 2) = 0,9231
- Återkallande = 24 ÷ (24 + 6) = 0,8
- F1 = 2 × (0,9231 × 0,8) ÷ (0,9231 + 0,8) = 0,8572
Som du ser ligger F1-värdet mellan värdena för precision och återkallande.
Även om F1-noggrannhet inte är lika lätt att förstå, bidrar det till att nyansera det grundläggande noggrannhetstalet. Det kan också hjälpa vid obalanserade datauppsättningar, som följande diskussion visar.
Avsnittet Modellens noggrannhet i det här ämnet jämförde de två följande sammanblandningsmatriserna. Även om den första modellen har lägre noggrannhet, ansågs den vara en mer användbar modell eftersom den visade mer förbättring än standardgissningen för betalning i tid.


Nu ska vi se hur de här två modellerna står sig i jämförelse med när F1-poängen används. F1-poängfaktorerna i precision och återkallande för varje tillstånd, och F1-makroberäkningen tar fram medelvärdet för F1-poäng för alla tillstånd för att fastställa en övergripande F1-poäng. Det finns andra F1-varianter, men det är av större intresse att ta hänsyn till makroversionen, med tanke på den lika behandling som ges för alla tre tillstånden.
För att förenkla beräkningarna skapades exempelmatriser som matchar de faktiska och förutsagda värdena. Dessa matriser använde sklearns metrics-biblioteket i Python för att beräkna värdena. Detta är resultatet.
| Modell | Naiv gissning | Precision | F1-makro |
|---|---|---|---|
| Modell 1 | 0.5 | 0.73 | 0.67 |
| Modell 2 | 0.80 | 0.83 | 0.66 |
Mer information om hur beräkningen fungerar finns i sklearn.metrics-klassificeringsrapporten för modell 1. De tre tillstånden, "i tid", "sent" och "mycket sent", representeras av de rader som är märkta 1, 2 och 3. Makromedelvärdet är bara genomsnittet för kolumnen "f1-score".
| precision | återkallande | f1-score | |
|---|---|---|---|
| 1 | 0.83 | 0.80 | 0.82 |
| 2 | 0.68 | 0.71 | 0.69 |
| 3 | 0.50 | 0.50 | 0.50 |
Som de här resultaten visar har de två modellerna nästan identiska F1-makropoäng för noggrannhet. I detta och många andra fall ger F1-noggrannhet en bättre indikator på modellens funktion. När det gäller noggrannhet kräver tolkningen av resultaten att du förstår vad som är viktigast att beakta i modellen.