Olika sätt att köra Resource Estimator
I den här artikeln lär du dig att arbeta med Azure Quantum Resource Estimator. Resource Estimator hjälper dig att uppskatta de resurser som krävs för att köra ett kvantprogram på en kvantdator. Du kan använda Resource Estimator för att uppskatta antalet kvantbitar, antalet portar och djupet i kretsen som krävs för att köra ett kvantprogram.
Resursberäknaren är tillgänglig i Visual Studio Code med tillägget Quantum Development Kit. Mer information finns i Installera Quantum Development Kit.
Varning
Resursberäknaren i Azure-portalen är inaktuell. Vi rekommenderar att du övergår till den lokala resursberäknaren i Visual Studio Code i Quantum Development Kit.
Krav för VS Code
- Den senaste versionen av Visual Studio Code eller öppna VS Code på webben.
- Den senaste versionen av-tillägget för
Quantum Development Kit. Installationsinformation finns i Konfigurera QDK-tillägget.
Dricks
Du behöver inte ha något Azure-konto för att köra resursberäknaren.
Skapa en ny Q#-fil
- Öppna Visual Studio Code och välj Fil > Ny textfil för att skapa en ny fil.
- Spara filen som
ShorRE.qs. Den här filen innehåller Q#-koden för ditt program.
Skapa kvantalgoritmen
Kopiera följande kod till ShorRE.qs filen:
import Std.Arrays.*;
import Std.Canon.*;
import Std.Convert.*;
import Std.Diagnostics.*;
import Std.Math.*;
import Std.Measurement.*;
import Microsoft.Quantum.Unstable.Arithmetic.*;
import Std.ResourceEstimation.*;
operation Main() : Unit {
let bitsize = 31;
// When choosing parameters for `EstimateFrequency`, make sure that
// generator and modules are not co-prime
let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize);
}
// In this sample we concentrate on costing the `EstimateFrequency`
// operation, which is the core quantum operation in Shors algorithm, and
// we omit the classical pre- and post-processing.
/// # Summary
/// Estimates the frequency of a generator
/// in the residue ring Z mod `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order (period)
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## bitsize
/// Number of bits needed to represent the modulus.
///
/// # Output
/// The numerator k of dyadic fraction k/2^bitsPrecision
/// approximating s/r.
operation EstimateFrequency(
generator : Int,
modulus : Int,
bitsize : Int
)
: Int {
mutable frequencyEstimate = 0;
let bitsPrecision = 2 * bitsize + 1;
// Allocate qubits for the superposition of eigenstates of
// the oracle that is used in period finding.
use eigenstateRegister = Qubit[bitsize];
// Initialize eigenstateRegister to 1, which is a superposition of
// the eigenstates we are estimating the phases of.
// We first interpret the register as encoding an unsigned integer
// in little endian encoding.
ApplyXorInPlace(1, eigenstateRegister);
let oracle = ApplyOrderFindingOracle(generator, modulus, _, _);
// Use phase estimation with a semiclassical Fourier transform to
// estimate the frequency.
use c = Qubit();
for idx in bitsPrecision - 1..-1..0 {
within {
H(c);
} apply {
// `BeginEstimateCaching` and `EndEstimateCaching` are the operations
// exposed by Azure Quantum Resource Estimator. These will instruct
// resource counting such that the if-block will be executed
// only once, its resources will be cached, and appended in
// every other iteration.
if BeginEstimateCaching("ControlledOracle", SingleVariant()) {
Controlled oracle([c], (1 <<< idx, eigenstateRegister));
EndEstimateCaching();
}
R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c);
}
if MResetZ(c) == One {
frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx);
}
}
// Return all the qubits used for oracles eigenstate back to 0 state
// using Microsoft.Quantum.Intrinsic.ResetAll.
ResetAll(eigenstateRegister);
return frequencyEstimate;
}
/// # Summary
/// Interprets `target` as encoding unsigned little-endian integer k
/// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where
/// p is `power`, g is `generator` and N is `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order ( period )
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## power
/// Power of `generator` by which `target` is multiplied.
/// ## target
/// Register interpreted as little endian encoded which is multiplied by
/// given power of the generator. The multiplication is performed modulo
/// `modulus`.
internal operation ApplyOrderFindingOracle(
generator : Int, modulus : Int, power : Int, target : Qubit[]
)
: Unit
is Adj + Ctl {
// The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We
// also use `ExpModI` to compute a by which x must be multiplied. Also
// note that we interpret target as unsigned integer in little-endian
// encoding.
ModularMultiplyByConstant(modulus,
ExpModI(generator, power, modulus),
target);
}
/// # Summary
/// Performs modular in-place multiplication by a classical constant.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(c*x) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular multiplication
/// ## c
/// Constant by which to multiply |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
use qs = Qubit[Length(y)];
for (idx, yq) in Enumerated(y) {
let shiftedC = (c <<< idx) % modulus;
Controlled ModularAddConstant([yq], (modulus, shiftedC, qs));
}
ApplyToEachCA(SWAP, Zipped(y, qs));
let invC = InverseModI(c, modulus);
for (idx, yq) in Enumerated(y) {
let shiftedC = (invC <<< idx) % modulus;
Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs));
}
}
/// # Summary
/// Performs modular in-place addition of a classical constant into a
/// quantum register.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(x+c) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular addition
/// ## c
/// Constant to add to |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
body (...) {
Controlled ModularAddConstant([], (modulus, c, y));
}
controlled (ctrls, ...) {
// We apply a custom strategy to control this operation instead of
// letting the compiler create the controlled variant for us in which
// the `Controlled` functor would be distributed over each operation
// in the body.
//
// Here we can use some scratch memory to save ensure that at most one
// control qubit is used for costly operations such as `AddConstant`
// and `CompareGreaterThenOrEqualConstant`.
if Length(ctrls) >= 2 {
use control = Qubit();
within {
Controlled X(ctrls, control);
} apply {
Controlled ModularAddConstant([control], (modulus, c, y));
}
} else {
use carry = Qubit();
Controlled AddConstant(ctrls, (c, y + [carry]));
Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry]));
Controlled AddConstant([carry], (modulus, y));
Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry));
}
}
}
/// # Summary
/// Performs in-place addition of a constant into a quantum register.
///
/// # Description
/// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive
/// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩.
///
/// # Input
/// ## c
/// Constant number to add to |𝑦⟩.
/// ## y
/// Quantum register of second summand and target; must not be empty.
internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl {
// We are using this version instead of the library version that is based
// on Fourier angles to show an advantage of sparse simulation in this sample.
let n = Length(y);
Fact(n > 0, "Bit width must be at least 1");
Fact(c >= 0, "constant must not be negative");
Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}");
if c != 0 {
// If c has j trailing zeroes than the j least significant bits
// of y won't be affected by the addition and can therefore be
// ignored by applying the addition only to the other qubits and
// shifting c accordingly.
let j = NTrailingZeroes(c);
use x = Qubit[n - j];
within {
ApplyXorInPlace(c >>> j, x);
} apply {
IncByLE(x, y[j...]);
}
}
}
/// # Summary
/// Performs greater-than-or-equals comparison to a constant.
///
/// # Description
/// Toggles output qubit `target` if and only if input register `x`
/// is greater than or equal to `c`.
///
/// # Input
/// ## c
/// Constant value for comparison.
/// ## x
/// Quantum register to compare against.
/// ## target
/// Target qubit for comparison result.
///
/// # Reference
/// This construction is described in [Lemma 3, arXiv:2201.10200]
internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit)
: Unit is Adj+Ctl {
let bitWidth = Length(x);
if c == 0 {
X(target);
} elif c >= 2 ^ bitWidth {
// do nothing
} elif c == 2 ^ (bitWidth - 1) {
ApplyLowTCNOT(Tail(x), target);
} else {
// normalize constant
let l = NTrailingZeroes(c);
let cNormalized = c >>> l;
let xNormalized = x[l...];
let bitWidthNormalized = Length(xNormalized);
let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized));
use qs = Qubit[bitWidthNormalized - 1];
let cs1 = [Head(xNormalized)] + Most(qs);
let cs2 = Rest(xNormalized);
within {
for i in IndexRange(gates) {
(gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]);
}
} apply {
ApplyLowTCNOT(Tail(qs), target);
}
}
}
/// # Summary
/// Internal operation used in the implementation of GreaterThanOrEqualConstant.
internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj {
within {
ApplyToEachA(X, [control1, control2]);
} apply {
ApplyAnd(control1, control2, target);
X(target);
}
}
internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit)
: Unit is Adj {
body (...) {
CCNOT(control1, control2, target);
}
adjoint (...) {
H(target);
if (M(target) == One) {
X(target);
CZ(control1, control2);
}
}
}
/// # Summary
/// Returns the number of trailing zeroes of a number
///
/// ## Example
/// ```qsharp
/// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0
/// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2
/// ```
internal function NTrailingZeroes(number : Int) : Int {
mutable nZeroes = 0;
mutable copy = number;
while (copy % 2 == 0) {
nZeroes += 1;
copy /= 2;
}
return nZeroes;
}
/// # Summary
/// An implementation for `CNOT` that when controlled using a single control uses
/// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7.
internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl {
body (...) {
CNOT(a, b);
}
adjoint self;
controlled (ctls, ...) {
// In this application this operation is used in a way that
// it is controlled by at most one qubit.
Fact(Length(ctls) <= 1, "At most one control line allowed");
if IsEmpty(ctls) {
CNOT(a, b);
} else {
use q = Qubit();
within {
ApplyAnd(Head(ctls), a, q);
} apply {
CNOT(q, b);
}
}
}
controlled adjoint self;
}
Kör resursberäknaren
Resource Estimator erbjuder sex fördefinierade qubitparametrar, varav fyra har gatebaserade instruktionsuppsättningar och två som har en Majorana-instruktionsuppsättning. Den erbjuder också två korrigeringskodersurface_code för kvantfel och floquet_code.
I det här exemplet kör du Resource Estimator med kvantbitsparametern qubit_gate_us_e3 och korrigeringskoden för surface_code kvantfel.
Välj Visa –> kommandopalett och skriv "resurs" som ska ta upp alternativet Q#: Beräkna resursuppskattningar . Du kan också klicka på Uppskatta från listan över kommandon som visas precis före åtgärden
Main. Välj det här alternativet om du vill öppna fönstret Resursberäknare.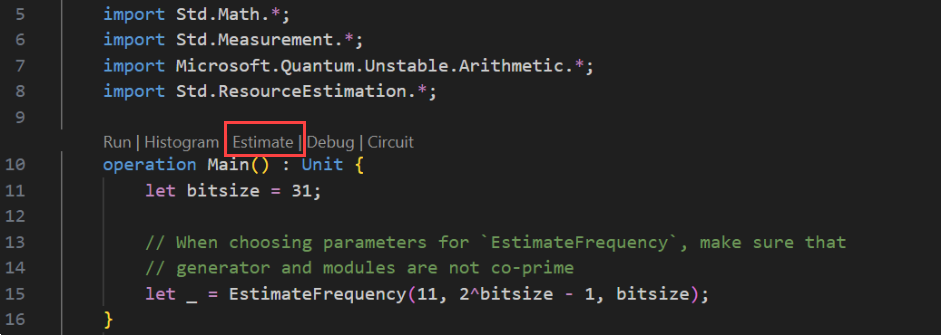
Du kan välja en eller flera qubitparameter + felkorrigeringskodtyper att uppskatta resurserna för. I det här exemplet väljer du qubit_gate_us_e3 och klickar på OK.
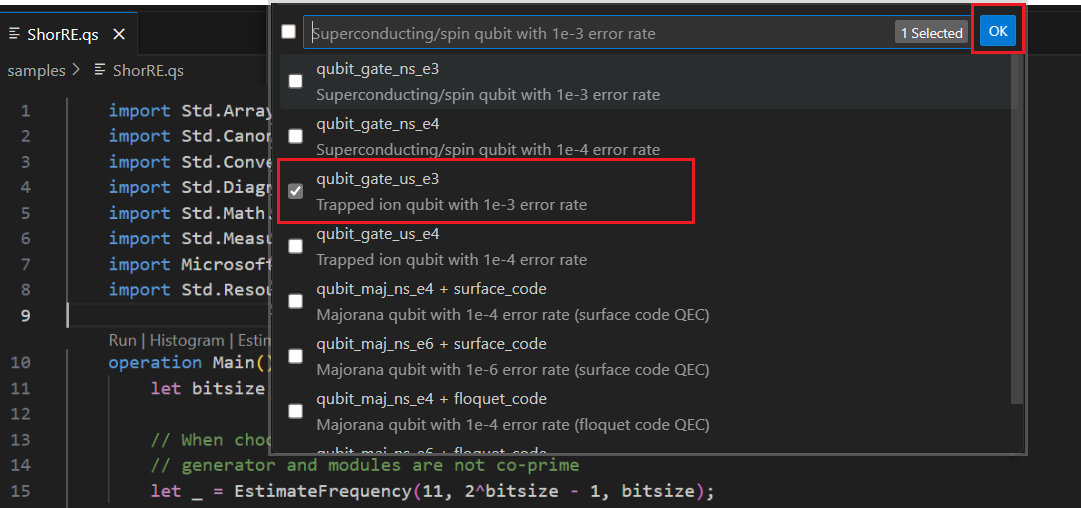
Ange felbudgeten eller acceptera standardvärdet 0.001. I det här exemplet lämnar du standardvärdet och trycker på Retur.
Tryck på Retur för att acceptera standardresultatnamnet baserat på filnamnet, i det här fallet ShorRE.
Visa resultatet
Resource Estimator innehåller flera uppskattningar för samma algoritm, var och en visar kompromisser mellan antalet kvantbitar och körningen. Att förstå kompromissen mellan körning och systemskala är en av de viktigaste aspekterna av resursuppskattning.
Resultatet av resursuppskattningen visas i fönstret Q#-uppskattning .
På fliken Resultat visas en sammanfattning av resursuppskattningen. Klicka på ikonen bredvid den första raden för att välja de kolumner som du vill visa. Du kan välja mellan körningsnamn, uppskattningstyp, kvantbitstyp, qec-schema, felbudget, logiska kvantbitar, logiskt djup, kodavstånd, T-tillstånd, T-fabriker, T-fabriksfraktion, körning, rQOPS och fysiska kvantbitar.
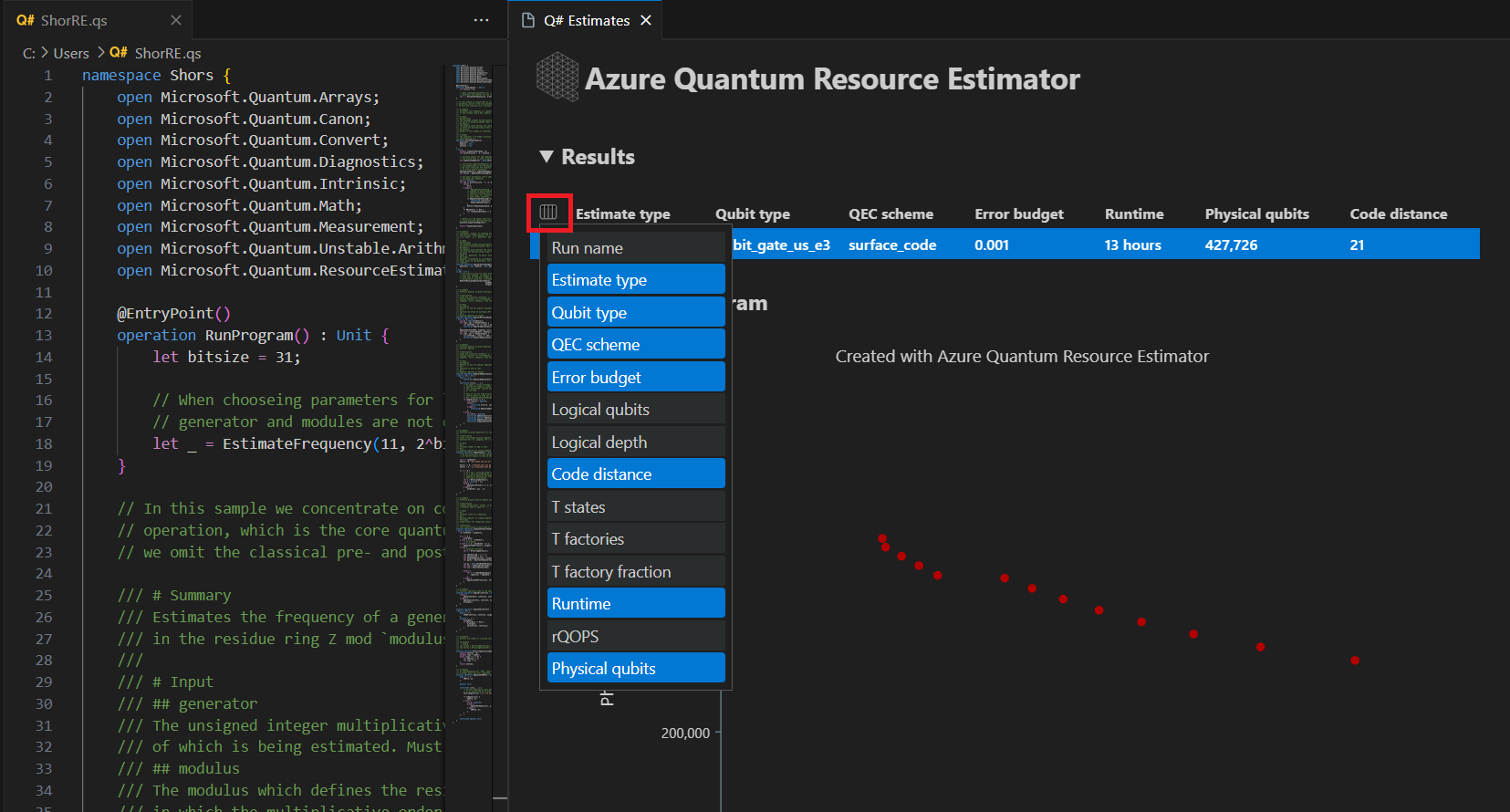
I kolumnen Uppskattningstyp i resultattabellen kan du se antalet optimala kombinationer av {antal qubits, runtime} för din algoritm. Dessa kombinationer kan visas i diagrammet för rumstid.
Diagrammet Space-time visar kompromisserna mellan antalet fysiska kvantbitar och algoritmens körning. I det här fallet hittar Resource Estimator 13 olika optimala kombinationer av många tusen möjliga kombinationer. Du kan hovra över varje {antal kvantbitar, runtime} punkt för att se information om resursuppskattningen vid den tidpunkten.
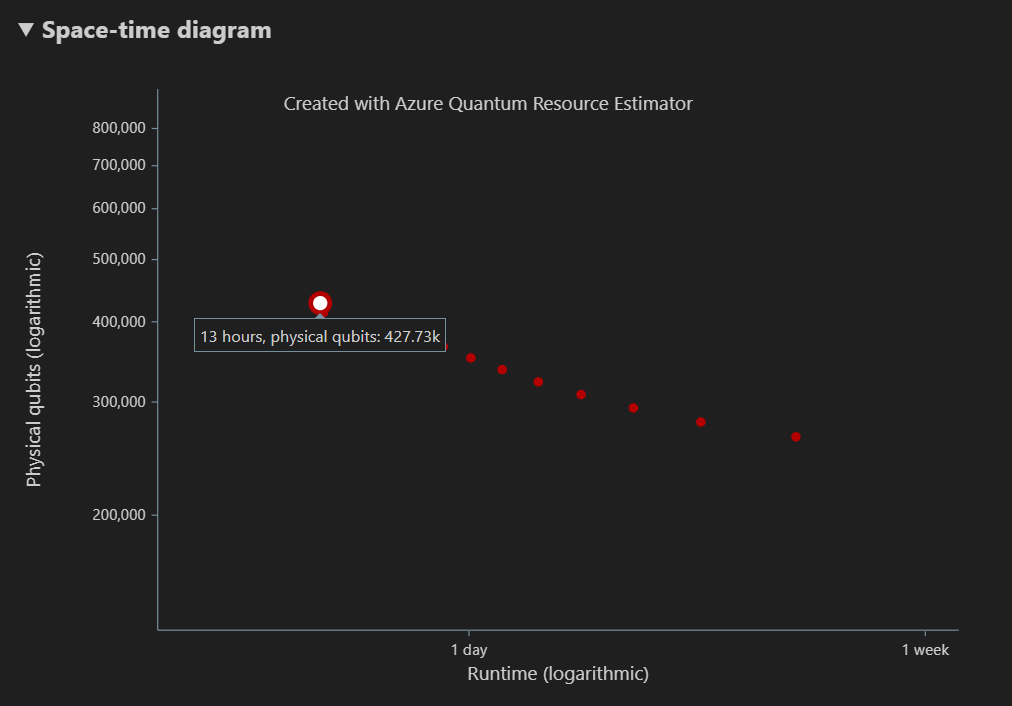
Mer information finns i Diagram över tidsrymd.
Kommentar
Du måste klicka på en punkt i tidsdiagrammet, dvs. ett {antal qubits, runtime}-par, för att se utrymmesdiagrammet och informationen om den resursuppskattning som motsvarar den punkten.
Diagrammet Utrymme visar fördelningen av fysiska kvantbitar som används för algoritmen och T-fabrikerna, vilket motsvarar ett {antal qubits, runtime}-par. Om du till exempel väljer den vänstra punkten i tidsdiagrammet är antalet fysiska kvantbitar som krävs för att köra algoritmen 427726, 196686 som är algoritmkvabits och 231040 som är T-fabriks qubitar.
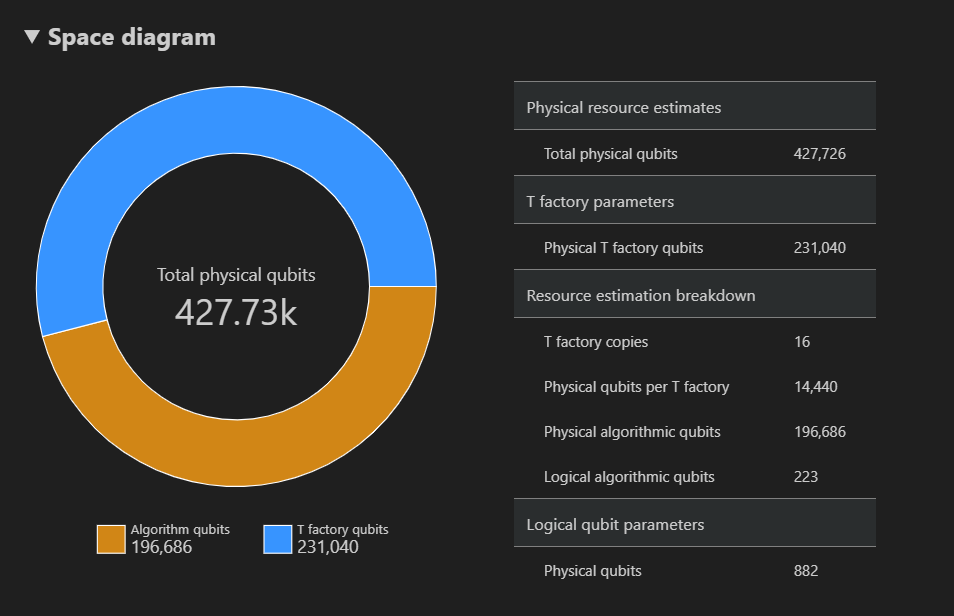
Slutligen visar fliken Resursuppskattningar den fullständiga listan över utdata för resursberäknaren som motsvarar ett {antal qubits, runtime}-par. Du kan kontrollera kostnadsinformationen genom att komprimera grupperna, som har mer information. Välj till exempel den vänstra punkten i diagrammet för utrymmestid och dölj gruppen Logiska qubitparametrar .
Logisk qubit-parameter Värde QEC-schema surface_code Kodavstånd 21 Fysiska kvantbitar 882 Logisk cykeltid 13 millisek Felfrekvens för logisk kvantbit 3.00E-13 Korsande förfaktor 0.03 Tröskelvärde för felkorrigering 0.01 Formel för logisk cykeltid (4 * twoQubitGateTime+ 2 *oneQubitMeasurementTime) *codeDistanceFormel för fysiska kvantbitar 2 * codeDistance*codeDistanceDricks
Klicka på Visa detaljerade rader för att visa beskrivningen av varje utdata för rapportdata.
Mer information finns i fullständiga rapportdata för Resource Estimator.
Ändra parametrarna target
Du kan beräkna kostnaden för samma Q#-program med hjälp av annan kvantbitstyp, felkorrigeringskod och felbudget. Öppna fönstret Resursberäknare genom att välja Visa –> kommandopalett och skriv Q#: Calculate Resource Estimates.
Välj valfri annan konfiguration, till exempel parametern Majorana-baserad qubit, qubit_maj_ns_e6. Acceptera standardvärdet för felbudget eller ange ett nytt och tryck på Retur. Resource Estimator kör uppskattningen igen med de nya target parametrarna.
Mer information finns i Target parametrar för Resource Estimator.
Köra flera konfigurationer av parametrar
Azure Quantum Resource Estimator kan köra flera konfigurationer av parametrar och jämföra resultatet av target resursuppskattningen.
Välj Visa –> Kommandopalett eller tryck på Ctrl+Skift+P och skriv
Q#: Calculate Resource Estimates.Välj qubit_gate_us_e3, qubit_gate_us_e4, qubit_maj_ns_e4 + floquet_code och qubit_maj_ns_e6 + floquet_code och klicka på OK.
Acceptera standardfelets budgetvärde 0.001 och tryck på Retur.
Tryck på Retur för att acceptera indatafilen, i det här fallet ShorRE.qs.
När det gäller flera konfigurationer av parametrar visas resultatet i olika rader på fliken Resultat .
Diagrammet Space-time visar resultatet för alla konfigurationer av parametrar. Den första kolumnen i resultattabellen visar förklaringen för varje konfiguration av parametrar. Du kan hovra över varje punkt för att se information om resursuppskattningen vid den tidpunkten.
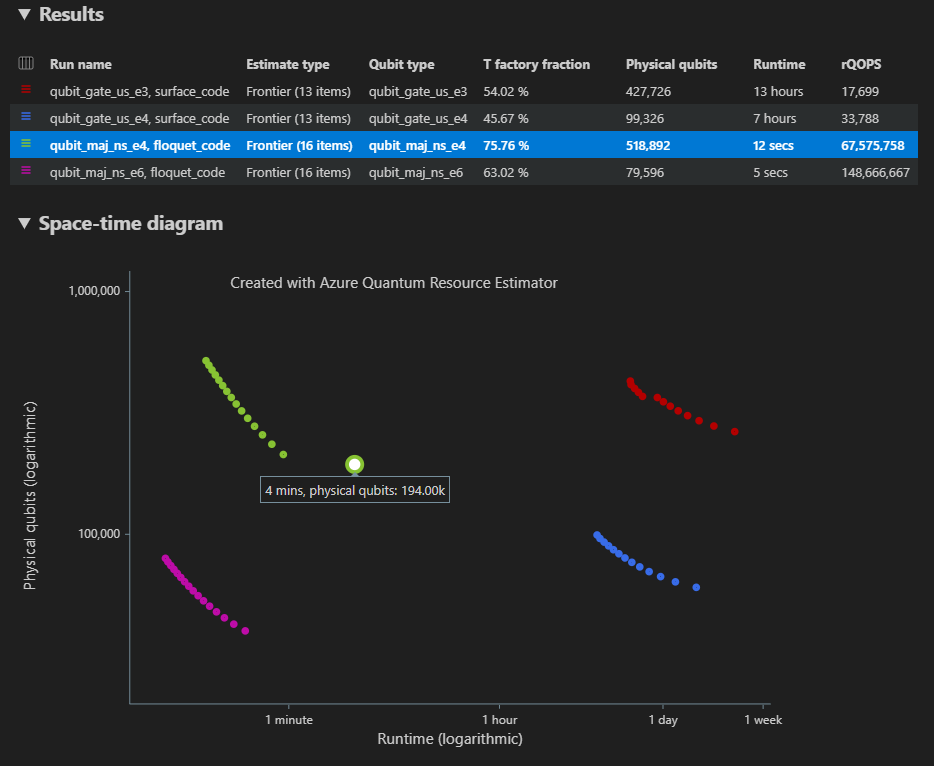
Klicka på en {antal qubits, runtime} i tidsdiagrammet för att hämta motsvarande utrymmesdiagram och rapportdata.
Förutsättningar för Jupyter Notebook i VS Code
En Python-miljö med Python och Pip installerade.
Den senaste versionen av Visual Studio Code eller öppna VS Code på webben.
VS Code med Quantum Development Kit, Pythonoch Jupyter-tillägg installerade.
De senaste Azure Quantum
qsharpochqsharp_widgetspaketen.python -m pip install --upgrade qsharp qsharp_widgetseller
!pip install --upgrade qsharp qsharp_widgets
Dricks
Du behöver inte ha något Azure-konto för att köra resursberäknaren.
Skapa kvantalgoritmen
I VS Code väljer du Visa > kommandopalett och väljer Skapa: Ny Jupyter Notebook.
I det övre högra hörnet identifierar och visar VS Code den version av Python och den virtuella Python-miljön som har valts för notebook-filen. Om du har flera Python-miljöer kan du behöva välja en kernel med hjälp av kernelväljaren längst upp till höger. Om ingen miljö har identifierats kan du läsa mer i Jupyter Notebooks i VS Code .
Importera paketet i den första cellen i notebook-filen
qsharp.import qsharpLägg till en ny cell och kopiera följande kod.
%%qsharp import Std.Arrays.*; import Std.Canon.*; import Std.Convert.*; import Std.Diagnostics.*; import Std.Math.*; import Std.Measurement.*; import Microsoft.Quantum.Unstable.Arithmetic.*; import Std.ResourceEstimation.*; operation RunProgram() : Unit { let bitsize = 31; // When choosing parameters for `EstimateFrequency`, make sure that // generator and modules are not co-prime let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize); } // In this sample we concentrate on costing the `EstimateFrequency` // operation, which is the core quantum operation in Shors algorithm, and // we omit the classical pre- and post-processing. /// # Summary /// Estimates the frequency of a generator /// in the residue ring Z mod `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order (period) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## bitsize /// Number of bits needed to represent the modulus. /// /// # Output /// The numerator k of dyadic fraction k/2^bitsPrecision /// approximating s/r. operation EstimateFrequency( generator : Int, modulus : Int, bitsize : Int ) : Int { mutable frequencyEstimate = 0; let bitsPrecision = 2 * bitsize + 1; // Allocate qubits for the superposition of eigenstates of // the oracle that is used in period finding. use eigenstateRegister = Qubit[bitsize]; // Initialize eigenstateRegister to 1, which is a superposition of // the eigenstates we are estimating the phases of. // We first interpret the register as encoding an unsigned integer // in little endian encoding. ApplyXorInPlace(1, eigenstateRegister); let oracle = ApplyOrderFindingOracle(generator, modulus, _, _); // Use phase estimation with a semiclassical Fourier transform to // estimate the frequency. use c = Qubit(); for idx in bitsPrecision - 1..-1..0 { within { H(c); } apply { // `BeginEstimateCaching` and `EndEstimateCaching` are the operations // exposed by Azure Quantum Resource Estimator. These will instruct // resource counting such that the if-block will be executed // only once, its resources will be cached, and appended in // every other iteration. if BeginEstimateCaching("ControlledOracle", SingleVariant()) { Controlled oracle([c], (1 <<< idx, eigenstateRegister)); EndEstimateCaching(); } R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c); } if MResetZ(c) == One { frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx); } } // Return all the qubits used for oracle eigenstate back to 0 state // using Microsoft.Quantum.Intrinsic.ResetAll. ResetAll(eigenstateRegister); return frequencyEstimate; } /// # Summary /// Interprets `target` as encoding unsigned little-endian integer k /// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where /// p is `power`, g is `generator` and N is `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order ( period ) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## power /// Power of `generator` by which `target` is multiplied. /// ## target /// Register interpreted as little endian encoded which is multiplied by /// given power of the generator. The multiplication is performed modulo /// `modulus`. internal operation ApplyOrderFindingOracle( generator : Int, modulus : Int, power : Int, target : Qubit[] ) : Unit is Adj + Ctl { // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We // also use `ExpModI` to compute a by which x must be multiplied. Also // note that we interpret target as unsigned integer in little-endian // encoding. ModularMultiplyByConstant(modulus, ExpModI(generator, power, modulus), target); } /// # Summary /// Performs modular in-place multiplication by a classical constant. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register |𝑦⟩, this operation /// computes `(c*x) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular multiplication /// ## c /// Constant by which to multiply |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { use qs = Qubit[Length(y)]; for (idx, yq) in Enumerated(y) { let shiftedC = (c <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, shiftedC, qs)); } ApplyToEachCA(SWAP, Zipped(y, qs)); let invC = InverseModI(c, modulus); for (idx, yq) in Enumerated(y) { let shiftedC = (invC <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs)); } } /// # Summary /// Performs modular in-place addition of a classical constant into a /// quantum register. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register |𝑦⟩, this operation /// computes `(x+c) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular addition /// ## c /// Constant to add to |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { body (...) { Controlled ModularAddConstant([], (modulus, c, y)); } controlled (ctrls, ...) { // We apply a custom strategy to control this operation instead of // letting the compiler create the controlled variant for us in which // the `Controlled` functor would be distributed over each operation // in the body. // // Here we can use some scratch memory to save ensure that at most one // control qubit is used for costly operations such as `AddConstant` // and `CompareGreaterThenOrEqualConstant`. if Length(ctrls) >= 2 { use control = Qubit(); within { Controlled X(ctrls, control); } apply { Controlled ModularAddConstant([control], (modulus, c, y)); } } else { use carry = Qubit(); Controlled AddConstant(ctrls, (c, y + [carry])); Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry])); Controlled AddConstant([carry], (modulus, y)); Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry)); } } } /// # Summary /// Performs in-place addition of a constant into a quantum register. /// /// # Description /// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive /// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩. /// /// # Input /// ## c /// Constant number to add to |𝑦⟩. /// ## y /// Quantum register of second summand and target; must not be empty. internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl { // We are using this version instead of the library version that is based // on Fourier angles to show an advantage of sparse simulation in this sample. let n = Length(y); Fact(n > 0, "Bit width must be at least 1"); Fact(c >= 0, "constant must not be negative"); Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}"); if c != 0 { // If c has j trailing zeroes than the j least significant bits // of y will not be affected by the addition and can therefore be // ignored by applying the addition only to the other qubits and // shifting c accordingly. let j = NTrailingZeroes(c); use x = Qubit[n - j]; within { ApplyXorInPlace(c >>> j, x); } apply { IncByLE(x, y[j...]); } } } /// # Summary /// Performs greater-than-or-equals comparison to a constant. /// /// # Description /// Toggles output qubit `target` if and only if input register `x` /// is greater than or equal to `c`. /// /// # Input /// ## c /// Constant value for comparison. /// ## x /// Quantum register to compare against. /// ## target /// Target qubit for comparison result. /// /// # Reference /// This construction is described in [Lemma 3, arXiv:2201.10200] internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit) : Unit is Adj+Ctl { let bitWidth = Length(x); if c == 0 { X(target); } elif c >= 2 ^ bitWidth { // do nothing } elif c == 2 ^ (bitWidth - 1) { ApplyLowTCNOT(Tail(x), target); } else { // normalize constant let l = NTrailingZeroes(c); let cNormalized = c >>> l; let xNormalized = x[l...]; let bitWidthNormalized = Length(xNormalized); let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized)); use qs = Qubit[bitWidthNormalized - 1]; let cs1 = [Head(xNormalized)] + Most(qs); let cs2 = Rest(xNormalized); within { for i in IndexRange(gates) { (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]); } } apply { ApplyLowTCNOT(Tail(qs), target); } } } /// # Summary /// Internal operation used in the implementation of GreaterThanOrEqualConstant. internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { within { ApplyToEachA(X, [control1, control2]); } apply { ApplyAnd(control1, control2, target); X(target); } } internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { body (...) { CCNOT(control1, control2, target); } adjoint (...) { H(target); if (M(target) == One) { X(target); CZ(control1, control2); } } } /// # Summary /// Returns the number of trailing zeroes of a number /// /// ## Example /// ```qsharp /// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0 /// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2 /// ``` internal function NTrailingZeroes(number : Int) : Int { mutable nZeroes = 0; mutable copy = number; while (copy % 2 == 0) { nZeroes += 1; copy /= 2; } return nZeroes; } /// # Summary /// An implementation for `CNOT` that when controlled using a single control uses /// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7. internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl { body (...) { CNOT(a, b); } adjoint self; controlled (ctls, ...) { // In this application this operation is used in a way that // it is controlled by at most one qubit. Fact(Length(ctls) <= 1, "At most one control line allowed"); if IsEmpty(ctls) { CNOT(a, b); } else { use q = Qubit(); within { ApplyAnd(Head(ctls), a, q); } apply { CNOT(q, b); } } } controlled adjoint self; }
Beräkna kvantalgoritmen
Nu beräknar du de fysiska resurserna för RunProgram åtgärden med hjälp av standardantagandena. Lägg till en ny cell och kopiera följande kod.
result = qsharp.estimate("RunProgram()")
result
Funktionen qsharp.estimate skapar ett resultatobjekt som kan användas för att visa en tabell med det totala antalet fysiska resurser. Du kan granska kostnadsinformationen genom att expandera grupperna, som har mer information. Mer information finns i fullständiga rapportdata för Resource Estimator.
Expandera till exempel Logiska qubitparametrar grupp för att se att kodavståndet är 21 och att antalet fysiska kvantbitar är 882.
| Logisk qubit-parameter | Värde |
|---|---|
| QEC-schema | surface_code |
| Kodavstånd | 21 |
| Fysiska kvantbitar | 882 |
| Logisk cykeltid | 8 millisek |
| Felfrekvens för logisk kvantbit | 3.00E-13 |
| Korsande förfaktor | 0.03 |
| Tröskelvärde för felkorrigering | 0.01 |
| Formel för logisk cykeltid | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Formel för fysiska kvantbitar | 2 * codeDistance * codeDistance |
Dricks
Om du vill ha en mer kompakt version av utdatatabellen kan du använda result.summary.
Blankstegsdiagram
Fördelningen av fysiska kvantbitar som används för algoritmen och T-fabrikerna är en faktor som kan påverka utformningen av algoritmen. Du kan använda qsharp-widgets paketet för att visualisera den här fördelningen för att bättre förstå de uppskattade utrymmeskraven för algoritmen.
from qsharp-widgets import SpaceChart, EstimateDetails
SpaceChart(result)
I det här exemplet är antalet fysiska kvantbitar som krävs för att köra algoritmen 829766, 196686 av vilka är algoritmens kvantbitar och 633080 som är T-fabriks qubitar.
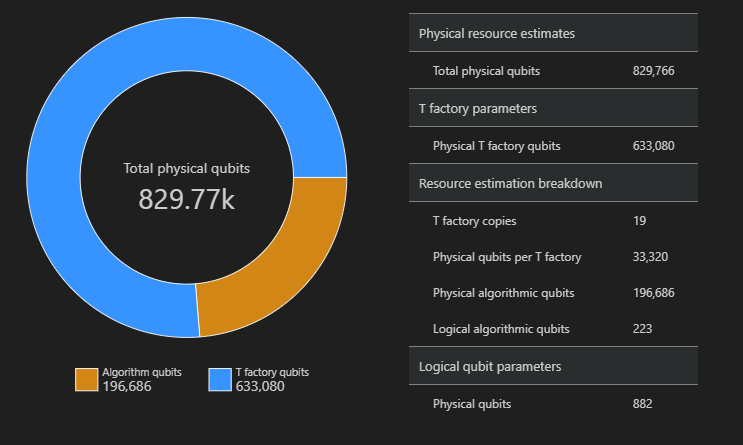
Ändra standardvärdena och uppskatta algoritmen
När du skickar en resursuppskattningsbegäran för ditt program kan du ange några valfria parametrar. Använd fältet jobParams för att komma åt alla target parametrar som kan skickas till jobbkörningen och se vilka standardvärden som antogs:
result['jobParams']
{'errorBudget': 0.001,
'qecScheme': {'crossingPrefactor': 0.03,
'errorCorrectionThreshold': 0.01,
'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
'name': 'surface_code',
'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
'qubitParams': {'instructionSet': 'GateBased',
'name': 'qubit_gate_ns_e3',
'oneQubitGateErrorRate': 0.001,
'oneQubitGateTime': '50 ns',
'oneQubitMeasurementErrorRate': 0.001,
'oneQubitMeasurementTime': '100 ns',
'tGateErrorRate': 0.001,
'tGateTime': '50 ns',
'twoQubitGateErrorRate': 0.001,
'twoQubitGateTime': '50 ns'}}
Du kan se att Resource Estimator tar qubit_gate_ns_e3 kvantbitsmodellen, felkorrigeringskoden surface_code och felbudgeten 0,001 som standardvärden för uppskattningen.
Det här är de target parametrar som kan anpassas:
-
errorBudget– den övergripande tillåtna felbudgeten för algoritmen -
qecScheme– QEC-schemat (Quantum Error Correction) -
qubitParams– de fysiska kvantbitsparametrarna -
constraints– begränsningarna på komponentnivå -
distillationUnitSpecifications- specifikationerna för algoritmer för destillation av T-fabriker -
estimateType- enkel eller gräns
Mer information finns i Target parametrar för Resource Estimator.
Ändra qubitmodell
Du kan beräkna kostnaden för samma algoritm med hjälp av parametern Majorana-baserad qubit, qubitParams, "qubit_maj_ns_e6".
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
}})
EstimateDetails(result_maj)
Ändra korrigeringsschema för kvantfel
Du kan köra resursuppskattningsjobbet igen för samma exempel på de Majorana-baserade qubitparametrarna med ett floqued QEC-schema, qecScheme.
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
},
"qecScheme": {
"name": "floquet_code"
}})
EstimateDetails(result_maj)
Budget för ändringsfel
Kör sedan om samma kvantkrets med errorBudget 10 %.
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
},
"qecScheme": {
"name": "floquet_code"
},
"errorBudget": 0.1})
EstimateDetails(result_maj)
Batchbearbetning med resursberäknaren
Med Azure Quantum Resource Estimator kan du köra flera konfigurationer av target parametrar och jämföra resultaten. Detta är användbart när du vill jämföra kostnaden för olika qubit-modeller, QEC-scheman eller felbudgetar.
Du kan utföra en batchuppskattning genom att skicka en lista med target parametrar till parametern
paramsförqsharp.estimatefunktionen. Kör till exempel samma algoritm med standardparametrarna och de Majorana-baserade qubitparametrarna med ett floquet QEC-schema.result_batch = qsharp.estimate("RunProgram()", params= [{}, # Default parameters { "qubitParams": { "name": "qubit_maj_ns_e6" }, "qecScheme": { "name": "floquet_code" } }]) result_batch.summary_data_frame(labels=["Gate-based ns, 10⁻³", "Majorana ns, 10⁻⁶"])Modell Logiska kvantbitar Logiskt djup T-tillstånd Kodavstånd T-fabriker T-fabriksfraktion Fysiska kvantbitar rQOPS Fysisk körning Grindbaserade ns, 10⁻³ 223 3,64 M 4,70 M 21 19 76.30 % 829.77k 26,55 M 31 sek Majorana ns, 10⁻⁶ 223 3,64 M 4,70 M 5 19 63.02 % 79.60k 148,67 M 5 sekunder Du kan också skapa en lista med uppskattningsparametrar med hjälp av
EstimatorParamsklassen.from qsharp.estimator import EstimatorParams, QubitParams, QECScheme, LogicalCounts labels = ["Gate-based µs, 10⁻³", "Gate-based µs, 10⁻⁴", "Gate-based ns, 10⁻³", "Gate-based ns, 10⁻⁴", "Majorana ns, 10⁻⁴", "Majorana ns, 10⁻⁶"] params = EstimatorParams(num_items=6) params.error_budget = 0.333 params.items[0].qubit_params.name = QubitParams.GATE_US_E3 params.items[1].qubit_params.name = QubitParams.GATE_US_E4 params.items[2].qubit_params.name = QubitParams.GATE_NS_E3 params.items[3].qubit_params.name = QubitParams.GATE_NS_E4 params.items[4].qubit_params.name = QubitParams.MAJ_NS_E4 params.items[4].qec_scheme.name = QECScheme.FLOQUET_CODE params.items[5].qubit_params.name = QubitParams.MAJ_NS_E6 params.items[5].qec_scheme.name = QECScheme.FLOQUET_CODEqsharp.estimate("RunProgram()", params=params).summary_data_frame(labels=labels)Modell Logiska kvantbitar Logiskt djup T-tillstånd Kodavstånd T-fabriker T-fabriksfraktion Fysiska kvantbitar rQOPS Fysisk körning Grindbaserade μs, 10⁻³ 223 3,64 M 4,70 M 17 13 40.54 % 216.77k 21.86k 10 timmar Grindbaserade μs, 10⁻⁴ 223 3,64 M 4,70 M 9 14 43.17 % 63.57k 41.30k 5 timmar Grindbaserade ns, 10⁻³ 223 3,64 M 4,70 M 17 16 69.08 % 416.89k 32,79 M 25 sekunder Gate-baserade ns, 10⁻⁴ 223 3,64 M 4,70 M 9 14 43.17 % 63.57k 61,94 M 13 sekunder Majorana ns, 10⁻⁴ 223 3,64 M 4,70 M 9 19 82.75 % 501.48k 82.59M 10 sekunder Majorana ns, 10⁻⁶ 223 3,64 M 4,70 M 5 13 31.47 % 42.96k 148,67 M 5 sekunder
Köra Pareto-gränsuppskattning
När du beräknar resurserna för en algoritm är det viktigt att överväga kompromissen mellan antalet fysiska kvantbitar och algoritmens körning. Du kan överväga allokering av så många fysiska kvantbitar som möjligt för att minska körningen av algoritmen. Antalet fysiska kvantbitar begränsas dock av antalet fysiska kvantbitar som är tillgängliga i kvantmaskinvaran.
Gränsuppskattningen Pareto ger flera uppskattningar för samma algoritm, var och en med en kompromiss mellan antalet kvantbitar och körningen.
Om du vill köra Resource Estimator med hjälp av Gränsen för Pareto måste du ange parametern
"estimateType"target som"frontier". Kör till exempel samma algoritm med de Majorana-baserade kvantbitsparametrarna med en ytkod med hjälp av Pareto-gränsuppskattning.result = qsharp.estimate("RunProgram()", params= {"qubitParams": { "name": "qubit_maj_ns_e4" }, "qecScheme": { "name": "surface_code" }, "estimateType": "frontier", # frontier estimation } )Du kan använda
EstimatesOverviewfunktionen för att visa en tabell med det totala antalet fysiska resurser. Klicka på ikonen bredvid den första raden för att välja de kolumner som du vill visa. Du kan välja mellan körningsnamn, uppskattningstyp, kvantbitstyp, qec-schema, felbudget, logiska kvantbitar, logiskt djup, kodavstånd, T-tillstånd, T-fabriker, T-fabriksfraktion, körning, rQOPS och fysiska kvantbitar.from qsharp_widgets import EstimatesOverview EstimatesOverview(result)
I kolumnen Skattningstyp i resultattabellen kan du se antalet olika kombinationer av {antal qubits, runtime} för din algoritm. I det här fallet hittar Resource Estimator 22 olika optimala kombinationer av många tusen möjliga kombinationer.
Diagram över tidsrymd
Funktionen EstimatesOverview visar också tidsdiagrammet för resursberäknaren.
Diagrammet för tidsrymd visar antalet fysiska kvantbitar och körningen av algoritmen för varje {antal qubits, runtime}-par. Du kan hovra över varje punkt för att se information om resursuppskattningen vid den tidpunkten.
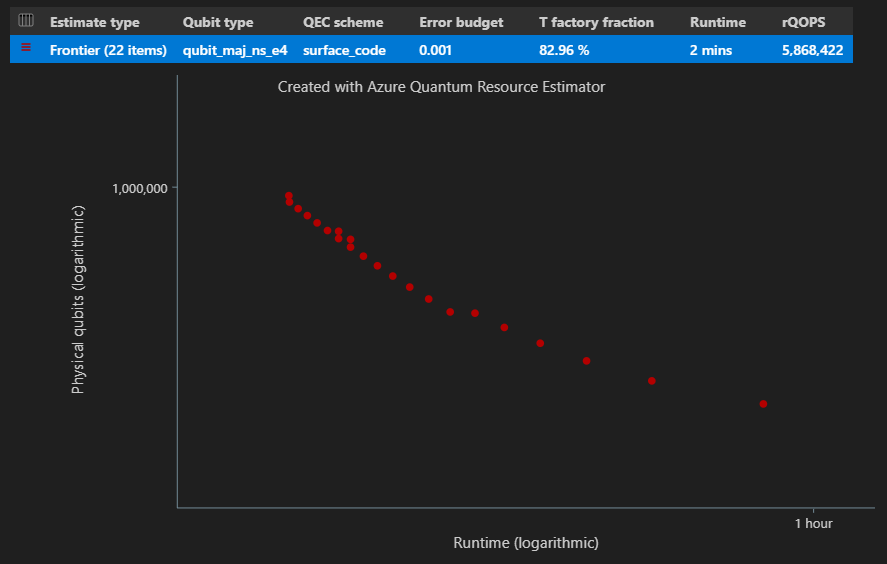
Batchbearbetning med Pareto-gränsuppskattning
Lägg till target parametrarna för att beräkna och jämföra flera konfigurationer av
"estimateType": "frontier",parametrar med gränsuppskattning.result = qsharp.estimate( "RunProgram()", [ { "qubitParams": { "name": "qubit_maj_ns_e4" }, "qecScheme": { "name": "surface_code" }, "estimateType": "frontier", # Pareto frontier estimation }, { "qubitParams": { "name": "qubit_maj_ns_e6" }, "qecScheme": { "name": "floquet_code" }, "estimateType": "frontier", # Pareto frontier estimation }, ] ) EstimatesOverview(result, colors=["#1f77b4", "#ff7f0e"], runNames=["e4 Surface Code", "e6 Floquet Code"])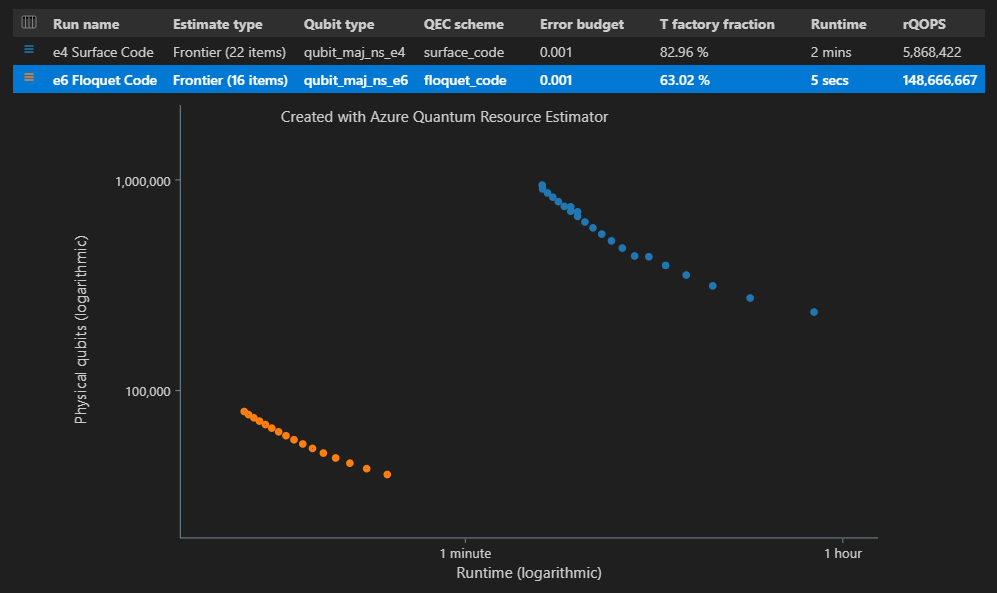
Kommentar
Du kan definiera färger och körningsnamn för kvantbitsdiagrammet med hjälp av
EstimatesOverviewfunktionen .När du kör flera konfigurationer av parametrar med hjälp av target Gränsen för Pareto kan du se resursuppskattningarna för en specifik punkt i tidsdiagrammet, dvs. för varje {antal qubits, runtime}-par. Följande kod visar till exempel användning av uppskattningsinformation för den andra körningen (estimate index=0) och den fjärde (punktindex=3) kortaste körningen.
EstimateDetails(result[1], 4)Du kan också se blankstegsdiagrammet för en viss punkt i diagrammet för tidsrymd. Följande kod visar till exempel blankstegsdiagrammet för den första körningen av kombinationer (estimate index=0) och den tredje kortaste körningen (punktindex=2).
SpaceChart(result[0], 2)
Krav för Qiskit i VS Code
En Python-miljö med Python och Pip installerade.
Den senaste versionen av Visual Studio Code eller öppna Visual Studio Code på webben.
VS Code med Quantum Development Kit, Pythonoch Jupyter-tillägg installerade.
De senaste Paketen för Azure Quantum
qsharpochqsharp_widgetsochqiskit.python -m pip install --upgrade qsharp qsharp_widgets qiskiteller
!pip install --upgrade qsharp qsharp_widgets qiskit
Dricks
Du behöver inte ha något Azure-konto för att köra resursberäknaren.
Skapa en ny Jupyter Notebook
- I VS Code väljer du Visa > kommandopalett och väljer Skapa: Ny Jupyter Notebook.
- I det övre högra hörnet identifierar och visar VS Code den version av Python och den virtuella Python-miljön som har valts för notebook-filen. Om du har flera Python-miljöer kan du behöva välja en kernel med hjälp av kernelväljaren längst upp till höger. Om ingen miljö har identifierats kan du läsa mer i Jupyter Notebooks i VS Code .
Skapa kvantalgoritmen
I det här exemplet skapar du en kvantkrets för en multiplikator baserat på konstruktionen som presenteras i Ruiz-Perez och Garcia-Escartin (arXiv:1411.5949) som använder Quantum Fourier Transform för att implementera aritmetik.
Du kan justera storleken på multiplikatorn genom att ändra variabeln bitwidth . Kretsgenereringen omsluts av en funktion som kan anropas med bitwidth multiplikatorns värde. Åtgärden kommer att ha två indataregister, var och en av de angivna bitwidth, och ett utdataregister som är dubbelt så stort som den angivna bitwidth. Funktionen skriver också ut vissa logiska resursantal för multiplikatorn som extraheras direkt från kvantkretsen.
from qiskit.circuit.library import RGQFTMultiplier
def create_algorithm(bitwidth):
print(f"[INFO] Create a QFT-based multiplier with bitwidth {bitwidth}")
circ = RGQFTMultiplier(num_state_qubits=bitwidth)
return circ
Kommentar
Om du väljer en Python-kernel och modulen qiskit inte känns igen kan du prova att välja en annan Python-miljö i kernelväljaren.
Beräkna kvantalgoritmen
Skapa en instans av algoritmen create_algorithm med hjälp av funktionen. Du kan justera storleken på multiplikatorn genom att ändra variabeln bitwidth .
bitwidth = 4
circ = create_algorithm(bitwidth)
Beräkna de fysiska resurserna för den här åtgärden med hjälp av standardantagandena. Du kan använda estimate-anropet, som är överbelastat för att acceptera ett QuantumCircuit objekt från Qiskit.
from qsharp.estimator import EstimatorParams
from qsharp.interop.qiskit import estimate
params = EstimatorParams()
result = estimate(circ, params)
Alternativt kan du använda ResourceEstimatorBackend för att utföra uppskattningen som den befintliga backenden gör.
from qsharp.interop.qiskit import ResourceEstimatorBackend
from qsharp.estimator import EstimatorParams
params = EstimatorParams()
backend = ResourceEstimatorBackend()
job = backend.run(circ, params)
result = job.result()
Objektet result innehåller utdata från resursuppskattningsjobbet. Du kan använda funktionen EstimateDetails för att visa resultatet i ett mer läsbart format.
from qsharp_widgets import EstimateDetails
EstimateDetails(result)
EstimateDetails-funktionen visar en tabell med det totala antalet fysiska resurser. Du kan granska kostnadsinformationen genom att expandera grupperna, som har mer information. Mer information finns i fullständiga rapportdata för Resource Estimator.
Om du till exempel expanderar logiska qubitparametrar grupp kan du enklare se att felkorrigeringskodavståndet är 15.
| Logisk qubit-parameter | Värde |
|---|---|
| QEC-schema | surface_code |
| Kodavstånd | 15 |
| Fysiska kvantbitar | 450 |
| Logisk cykeltid | 6us |
| Felfrekvens för logisk kvantbit | 3.00E-10 |
| Korsande förfaktor | 0.03 |
| Tröskelvärde för felkorrigering | 0.01 |
| Formel för logisk cykeltid | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Formel för fysiska kvantbitar | 2 * codeDistance * codeDistance |
I gruppen Fysiska kvantbitsparametrar kan du se de fysiska qubitegenskaper som antogs för den här uppskattningen. Till exempel antas tiden för att utföra en enda kvantbitsmätning och en en qubitsgrind vara 100 ns respektive 50 ns.
Dricks
Du kan också komma åt utdata från Resource Estimator som en Python-ordlista med hjälp av metoden result.data(). Om du till exempel vill komma åt det fysiska antalet result.data()["physicalCounts"].
Blankstegsdiagram
Fördelningen av fysiska kvantbitar som används för algoritmen och T-fabrikerna är en faktor som kan påverka utformningen av algoritmen. Du kan visualisera den här distributionen för att bättre förstå de uppskattade utrymmeskraven för algoritmen.
from qsharp_widgets import SpaceChart
SpaceChart(result)
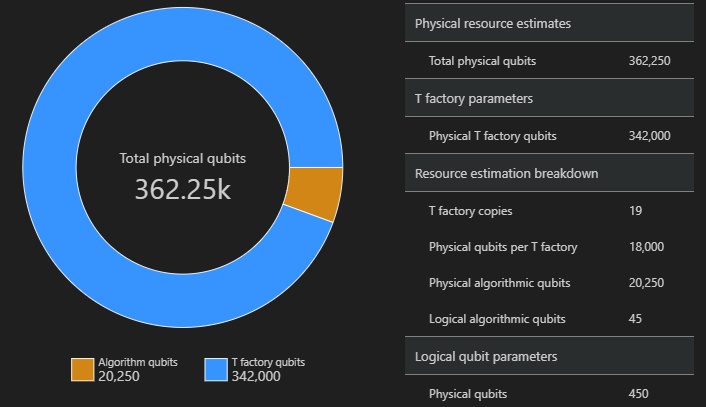
Blankstegsdiagrammet visar andelen kvantbitar för algoritmer och T Factory-kvantbitar. Observera att antalet kopior av T-fabriker, 19, bidrar till det totala antalet fysiska kvantbitar för T-fabriker, där $\text{T-fabriker} \cdot \text{fysisk kvantbit per T-fabrik}= 19 \cdot 18 000 = 342 000$.
Mer information finns i Fysisk uppskattning av T-fabriken.
Ändra standardvärdena och uppskatta algoritmen
När du skickar en resursuppskattningsbegäran för ditt program kan du ange några valfria parametrar. Använd fältet jobParams för att komma åt alla värden som kan skickas till jobbkörningen och se vilka standardvärden som antogs:
result.data()["jobParams"]
{'errorBudget': 0.001,
'qecScheme': {'crossingPrefactor': 0.03,
'errorCorrectionThreshold': 0.01,
'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
'name': 'surface_code',
'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
'qubitParams': {'instructionSet': 'GateBased',
'name': 'qubit_gate_ns_e3',
'oneQubitGateErrorRate': 0.001,
'oneQubitGateTime': '50 ns',
'oneQubitMeasurementErrorRate': 0.001,
'oneQubitMeasurementTime': '100 ns',
'tGateErrorRate': 0.001,
'tGateTime': '50 ns',
'twoQubitGateErrorRate': 0.001,
'twoQubitGateTime': '50 ns'}}
Det här är de target parametrar som kan anpassas:
-
errorBudget– den övergripande tillåtna felbudgeten -
qecScheme– QEC-schemat (Quantum Error Correction) -
qubitParams– de fysiska kvantbitsparametrarna -
constraints– begränsningarna på komponentnivå -
distillationUnitSpecifications- specifikationerna för algoritmer för destillation av T-fabriker
Mer information finns i Target parametrar för Resource Estimator.
Ändra qubitmodell
Beräkna sedan kostnaden för samma algoritm med hjälp av den Majorana-baserade kvantbitsparametern qubit_maj_ns_e6
qubitParams = {
"name": "qubit_maj_ns_e6"
}
result = backend.run(circ, qubitParams).result()
Du kan inspektera det fysiska antalet programmatiskt. Du kan till exempel utforska information om T-fabriken som skapades för att köra algoritmen.
result.data()["tfactory"]
{'eccDistancePerRound': [1, 1, 5],
'logicalErrorRate': 1.6833177305222897e-10,
'moduleNamePerRound': ['15-to-1 space efficient physical',
'15-to-1 RM prep physical',
'15-to-1 RM prep logical'],
'numInputTstates': 20520,
'numModulesPerRound': [1368, 20, 1],
'numRounds': 3,
'numTstates': 1,
'physicalQubits': 16416,
'physicalQubitsPerRound': [12, 31, 1550],
'runtime': 116900.0,
'runtimePerRound': [4500.0, 2400.0, 110000.0]}
Kommentar
Som standard visas körning i nanosekunder.
Du kan använda dessa data för att skapa några förklaringar av hur T-fabrikerna producerar de T-tillstånd som krävs.
data = result.data()
tfactory = data["tfactory"]
breakdown = data["physicalCounts"]["breakdown"]
producedTstates = breakdown["numTfactories"] * breakdown["numTfactoryRuns"] * tfactory["numTstates"]
print(f"""A single T factory produces {tfactory["logicalErrorRate"]:.2e} T states with an error rate of (required T state error rate is {breakdown["requiredLogicalTstateErrorRate"]:.2e}).""")
print(f"""{breakdown["numTfactories"]} copie(s) of a T factory are executed {breakdown["numTfactoryRuns"]} time(s) to produce {producedTstates} T states ({breakdown["numTstates"]} are required by the algorithm).""")
print(f"""A single T factory is composed of {tfactory["numRounds"]} rounds of distillation:""")
for round in range(tfactory["numRounds"]):
print(f"""- {tfactory["numUnitsPerRound"][round]} {tfactory["unitNamePerRound"][round]} unit(s)""")
A single T factory produces 1.68e-10 T states with an error rate of (required T state error rate is 2.77e-08).
23 copies of a T factory are executed 523 time(s) to produce 12029 T states (12017 are required by the algorithm).
A single T factory is composed of 3 rounds of distillation:
- 1368 15-to-1 space efficient physical unit(s)
- 20 15-to-1 RM prep physical unit(s)
- 1 15-to-1 RM prep logical unit(s)
Ändra korrigeringsschema för kvantfel
Kör nu resursuppskattningsjobbet igen för samma exempel på De Majorana-baserade qubitparametrarna med ett floqued QEC-schema, qecScheme.
params = {
"qubitParams": {"name": "qubit_maj_ns_e6"},
"qecScheme": {"name": "floquet_code"}
}
result_maj_floquet = backend.run(circ, params).result()
EstimateDetails(result_maj_floquet)
Budget för ändringsfel
Nu kör vi samma kvantkrets igen med errorBudget 10 %.
params = {
"errorBudget": 0.01,
"qubitParams": {"name": "qubit_maj_ns_e6"},
"qecScheme": {"name": "floquet_code"},
}
result_maj_floquet_e1 = backend.run(circ, params).result()
EstimateDetails(result_maj_floquet_e1)
Kommentar
Om du stöter på problem när du arbetar med Resursberäknaren kan du gå till sidan Felsökning eller kontakta AzureQuantumInfo@microsoft.com.