Teori om Grover sökalgoritm
I den här artikeln hittar du en detaljerad teoretisk förklaring av de matematiska principer som får Grover-algoritmen att fungera.
En praktisk implementering av Grover-algoritmen för att lösa matematiska problem finns i Implementera Grover sökalgoritm.
Förklaring av problemet
Grover-algoritmen påskyndar lösningen på ostrukturerade datasökningar (eller sökproblem) och kör sökningen i färre steg än någon klassisk algoritm kunde. Alla sökuppgifter kan uttryckas med en abstrakt funktion $f(x)$ som accepterar sökobjekt $x$. Om objektet $x$ är en lösning på sökaktiviteten, f $(x)=1$. Om objektet $x$ inte är en lösning, så $f(x)=0$. Sökproblemet består av att hitta alla objekt $x_0$ så att $f(x_0)=1$.
Alla problem som gör att du kan kontrollera om ett angivet värde $x$ är en giltig lösning (en " Ja eller inga problem") kan formuleras i termer av sökproblemet. Följande är några exempel:
- Booleskt problem med nöjdhet: Med tanke på en uppsättning booleska värden uppfyller uppsättningen en viss boolesk formel?
- Ambulerande försäljarproblemet: Vad är den kortaste möjliga rutten som förbinder alla städer?
- Problem med databassökning: Innehåller en databastabell posten $x$?
- Problem med heltalsfaktorisering: Är talet $N$ delbart med talet $x$?
Uppgiften som Grover-algoritmen syftar till att lösa kan uttryckas på följande sätt: med tanke på en klassisk funktion $f(x):\{0,1\}^n \rightarrow\{0,1\}$, där $n$ är bitstorleken för sökområdet, hittar du en indata $x_0$ som $f(x_0)=1$. Algoritmens komplexitet mäts med antalet användningsområden för funktionen $f(x)$. Klassiskt, i värsta fall, $måste f(x)$ utvärderas totalt $N-1$ gånger, där $N=2^n$, prova alla möjligheter. Efter $N-1-element$ måste det vara det sista elementet. Grover kvantalgoritm kan lösa detta problem mycket snabbare, vilket ger en kvadratisk hastighet upp. Kvadratiska här innebär att endast om $\sqrt{N}$ utvärderingar skulle krävas, jämfört $med N$.
Beskrivning av algoritmen
Anta att det finns $N 2^n= berättigade objekt för sökaktiviteten och att de indexeras genom att tilldela varje objekt ett heltal från $0$ till $N-1$$. Anta vidare att det finns $M$ olika giltiga indata, vilket innebär att det finns $M-indata$ som $f(x)=1$ för. Stegen i algoritmen är sedan följande:
- Börja med ett register över $n$ qubits som initierats i tillståndet $\ket{0}$.
- Förbered registret i en enhetlig superposition genom att tillämpa $H$ på varje qubit i registret: $$|\text{registrera}\rangle=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}|x\rangle$$
- Tillämpa följande åtgärder på registret $N_{\text{optimalt}}$ antal gånger:
- Fasoraklet $O_f$ som tillämpar en villkorsstyrd fasförskjutning på $-1$ för lösningsobjekten.
- Tillämpa $H$ på varje qubit i registret.
- En villkorlig fasförskjutning på $-1$ till varje beräkningsbastillstånd förutom $\ket{0}$. Detta kan representeras av den enhetliga åtgärden $-O_0$, eftersom $O_0$ representerar villkorsfasens övergång till $\ket{0}$ endast.
- Tillämpa $H$ på varje qubit i registret.
- Mät registret för att hämta indexet för ett objekt som är en lösning med mycket hög sannolikhet.
- Kontrollera om det är en giltig lösning. Annars startar du igen.
$N_{\text{optimal}}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}–\frac{{1}{{2}\right\rgolv$ är det optimala antalet iterationer som maximerar sannolikheten för att få rätt objekt genom att mäta registret.
Kommentar
Den gemensamma tillämpningen av steg 3.b, 3.c och 3.d kallas vanligtvis Grover diffusionsoperator.
Den övergripande enhetsåtgärden som tillämpas på registret är:
$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{optimal}}}H^{\otimes n}$$
Följa registrets tillstånd steg för steg
För att illustrera processen ska vi följa de matematiska omvandlingarna av registrets tillstånd för ett enkelt fall där det bara finns två kvantbitar och det giltiga elementet är $\ket{01}.$
Registret startar i det tillståndet:
$$\ket{\text{registrera}}=\ket{{00}$$
När du har tillämpat $H$ på varje kvantbit omvandlas registrets tillstånd till:
$$\ket{\text{registrera}}=\frac{{1}{\sqrt{4}}\sum_{i \in \lbrace 0,1 \rklammerparenteser}^2\ket{i}=\frac12(\ket{00}+\ket{01}+\ket{{10}+\ket{11})$$
Sedan tillämpas fasoraklet för att hämta:
$$\ket{\text{registrera}}=\frac12(\ket{{00}-\ket{{01}+\ket{{10}+\ket{{11})$$
Sedan agerar $H$ på varje qubit igen för att ge:
$$\ket{\text{registrera}}=\frac12(\ket{{00}+\ket{{01}-\ket{{10}+\ket{{11})$$
Nu tillämpas villkorsfasens skift på alla tillstånd utom $\ket{00}$:
$$\ket{\text{registrera}}=\frac12(\ket{{00}-\ket{{01}+\ket{{10}-\ket{{11})$$
Slutligen avslutas den första Grover-iterationen genom att tillämpa $H$ igen för att hämta:
$$\ket{\text{registrera}}=\ket{{01}$$
Genom att följa stegen ovan finns det giltiga objektet i en enda iteration. Som du ser senare beror det på att för N=4 och ett enda giltigt objekt är det optimala antalet gånger $N_{\text{optimalt}}=1$.
Geometrisk förklaring
För att se varför Grover-algoritmen fungerar ska vi studera algoritmen ur ett geometriskt perspektiv. Anta att det finns $M$ giltiga lösningar, superpositionen av alla kvanttillstånd som inte är en lösning på sökproblemet:
$$\ket{\text{dålig}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$
Superpositionen av alla tillstånd som är en lösning på sökproblemet:
$$\ket{\text{bra}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$
Eftersom bra och dåliga är ömsesidigt uteslutande uppsättningar eftersom ett objekt inte kan vara giltigt och inte giltigt, är tillstånden ortoggonala. Båda tillstånden utgör den ortoggonala grunden för ett plan i vektorutrymmet. Man kan använda det här planet för att visualisera algoritmen.
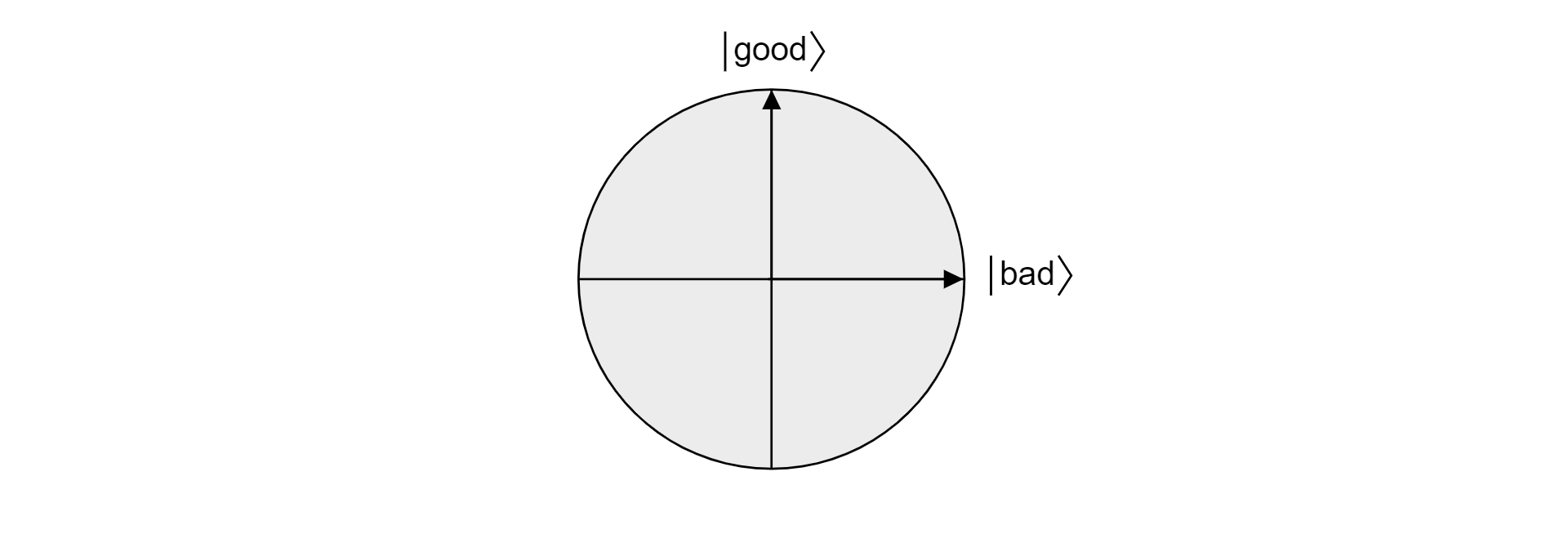
Anta nu $\ket{\psi}$ att det är ett godtyckligt tillstånd som lever i planet som spänns över av $\ket{\text{gott}}$ och $\ket{\text{ont}}$. Alla stater som bor i planet kan uttryckas som:
$$\ket{\psi} = \alpha \ket{\text{bra}} + \beta\ket{\text{dåligt}}$$
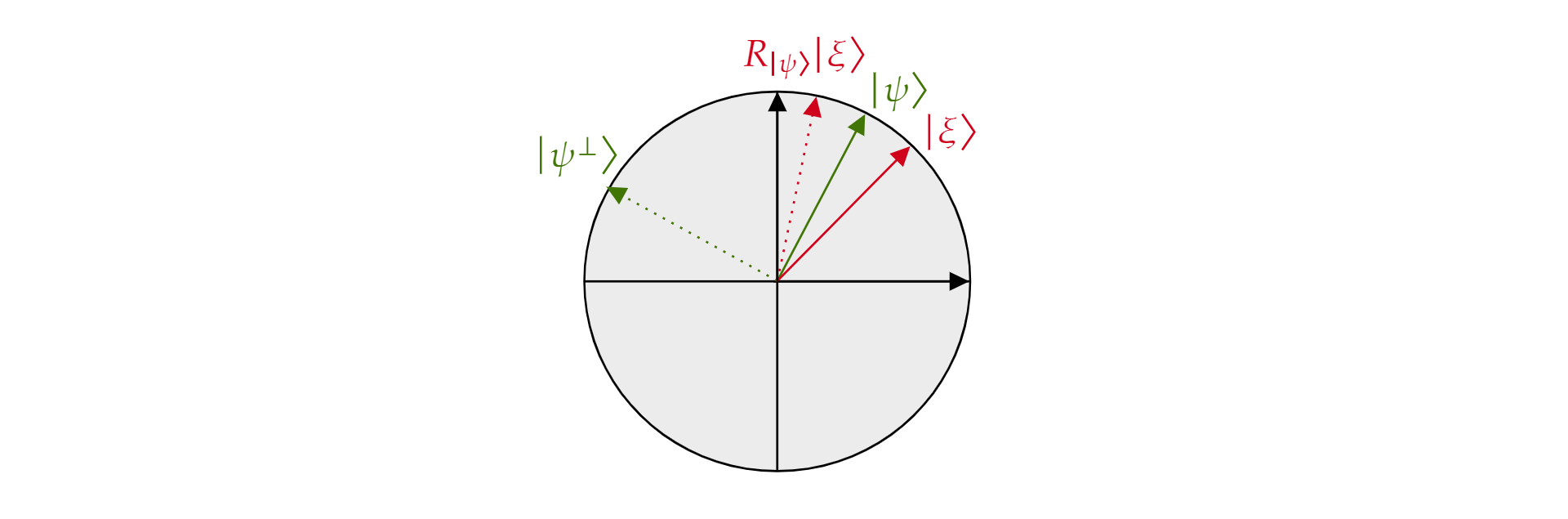
där $\alpha$ och $\beta$ är verkliga tal. Nu ska vi introducera reflektionsoperatorn $R_{\ket{\psi}}$, där $\ket{\psi}$ är något qubittillstånd som bor i planet. Operatorn definieras som:
$$ {\ket{\psi}}=R_2\ket{\psi}\bra{\psi}-\mathcal{I}$$
Det kallas reflektionsoperatorn om $\ket{\psi}$ eftersom det kan tolkas geometriskt som reflektion om riktningen $\ket{\psi}$för . Om du vill se det tar du den ortoggonala grunden för planet som bildas av $\ket{\psi}$ och dess ortoggonala komplement $\ket{\psi^{\perp}}$. Alla tillstånd $\ket{\xi}$ av planet kan brytas ned på följande sätt:
$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$
Om man tillämpar operatorn $R_{\ket{\psi}}$ på $\ket{\xi}$:
$$ {\ket{\psi}}\ket{R_\xi}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$
Operatorn $R_{\ket{\psi}}$ invertera komponenten ortogonial till $\ket{\psi}$ men lämnar komponenten $\ket{\psi}$ oförändrad. $Därför är R_{\ket{\psi}}$ en reflektion över $\ket{\psi}$.
Grover-algoritmen börjar efter den första tillämpningen av $H$ på varje qubit med en enhetlig superposition av alla tillstånd. Detta kan skrivas som:
$$\ket{\text{alla}}=\sqrt{\frac{M}{N}}\ket{\text{bra}} + \sqrt{\frac{N-M}{N}}\ket{\text{dåligt}}$$
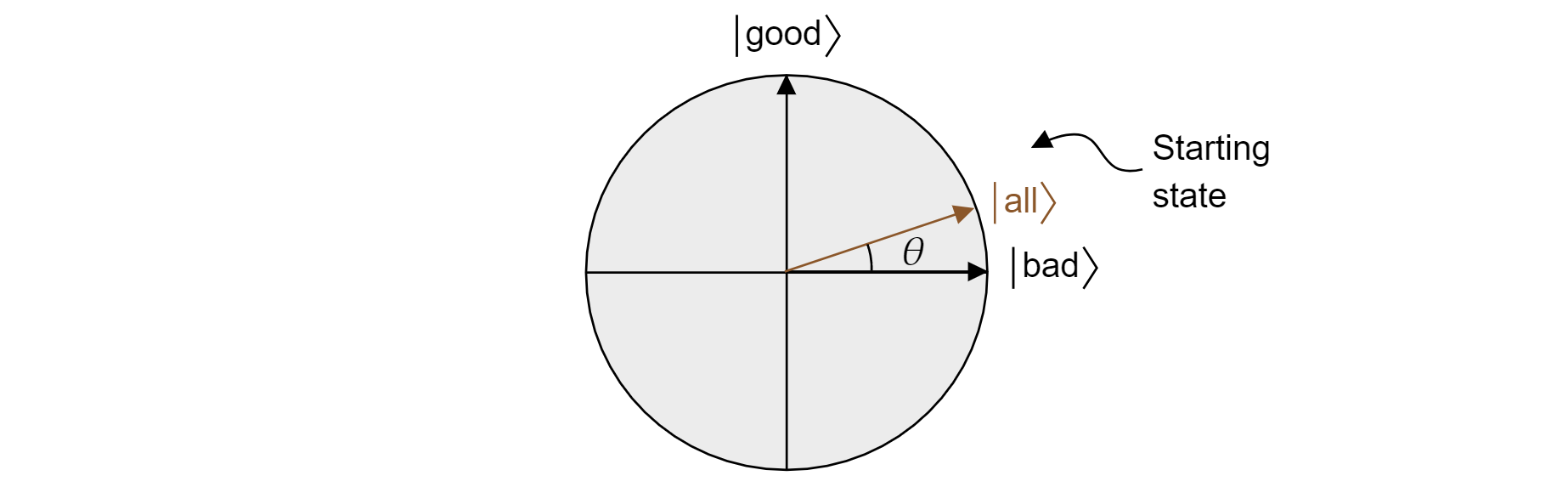
Och därmed bor staten i planet. Observera att sannolikheten för att få ett korrekt resultat vid mätning från samma superposition bara $|\bra{\text{är bra}}\ket{\text{alla}}|^2=M/N$, vilket är vad du kan förvänta dig av en slumpmässig gissning.
Oraklet $O_f$ lägger till en negativ fas i alla lösningar på sökproblemet. Därför kan den skrivas som en reflektion över den $\ket{\text{felaktiga}}$ axeln:
$$O_f = R_{\ket{\text{dålig}}}= 2\ket{\text{dålig}}\bra{\text{dålig}} - \mathbb{jag}$$
På motsvarande sätt är den villkorsstyrda fasförskjutningen $O_0$ bara en inverterad reflektion om tillståndet $\ket{0}$:
$$O_{0}= R_{\ket{0}}= -2\ket{{0}\bra{{0} + \mathbb{}$$
När man känner till detta är det lätt att kontrollera att Grover-diffusionsoperationen $-H^{\otimes n} O_{0} H^{\otimes n}$ också är en reflektion kring tillståndet $\ket{alla}$. Gör bara:
$$-H^{\otimes n} O_{{0} H^{\otimes n}=2H^{\otimes n}\ket{0}\bra{{0}H^{\otimes n} -H^{\otimes n}\mathbb{I}H^{\otimes n}= 2\ket{\text{alla}}\bra{\text{alla}} - \mathbb{jag}= R_{\ket{\text{alla}}}$$
Det har visats att varje iteration av Grover-algoritmen är en sammansättning av två reflektioner $R_{\ket{\text{bad}}}$ och $R_{\ket{\text{alla}}}$.
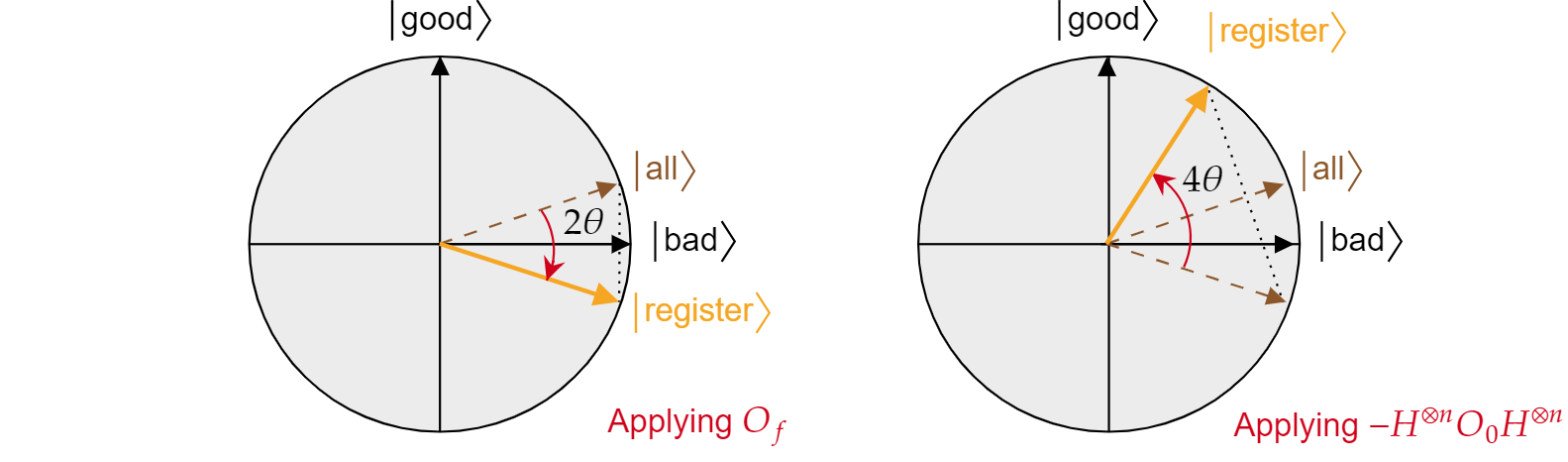
Den kombinerade effekten av varje Grover-iteration är en motsolsrotering av en vinkel $2\theta$. Lyckligtvis är vinkeln $\theta$ lätt att hitta. Eftersom $\theta$ bara är vinkeln mellan $\ket{\text{allt}}$ och $\ket{\text{dåligt}}$ kan man använda den skalära produkten för att hitta vinkeln. Det är känt att $\cos{\theta}=\braket{\text{alla}|\text{är dåliga}}$, så man måste beräkna $\braket{\text{alla}|\text{dåliga}}$. Från nedbrytningen av $\ket{\text{alla}}$ när det gäller $\ket{\text{dåligt}}$ och $\ket{\text{gott}}$ följer det:
$$\theta = \arccos{\left(\braket{\text{alla}|\text{dåliga}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$
Vinkeln mellan registrets tillstånd och det $\ket{\text{goda}}$ tillståndet minskar med varje iteration, vilket resulterar i en högre sannolikhet att mäta ett giltigt resultat. För att beräkna sannolikheten behöver du bara beräkna $|\braket{\text{ett bra}|\text{register}}|^2$. Vinkeln mellan $\ket{\text{god}}$ och $\ket{\text{register}}$ anges som $\gamma (k)$, där $k$ är iterationsräkningen.
$$\gamma = \frac{\pi}{2}-\theta -2k\theta =\frac{\pi}{{2} -(2k + 1) \theta $$
Sannolikheten för att lyckas är därför:
$$P(\text{success}) = \cos^2((\gammak)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$
Optimalt antal iterationer
Eftersom sannolikheten för framgång kan skrivas som en funktion av antalet iterationer kan det optimala antalet iterationer $N_{\text{optimal}}$ hittas genom att beräkna det minsta positiva heltal som (ungefär) maximerar sannolikhetsfunktionen för lyckade resultat.
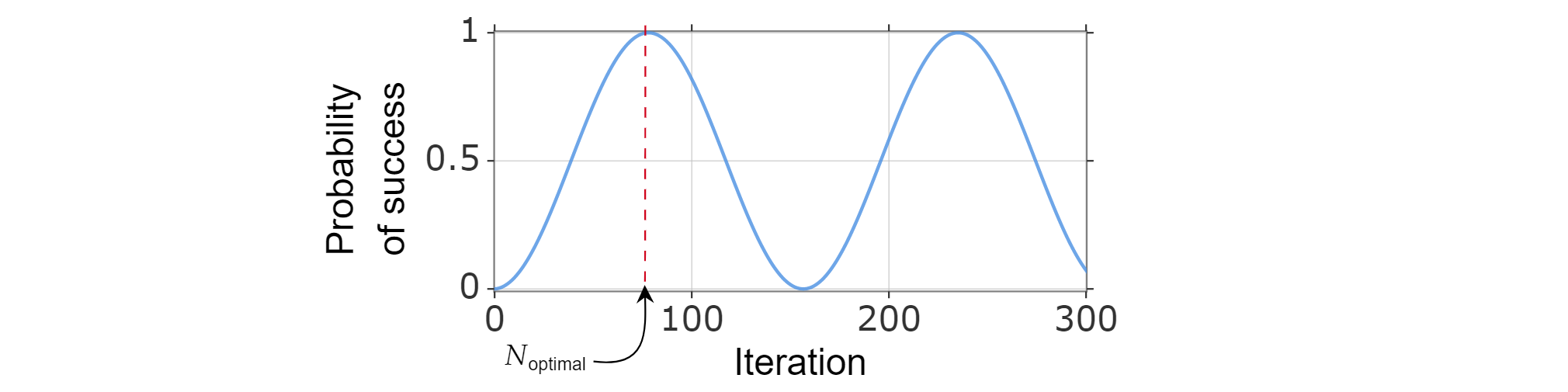
Det är känt att $\sin^2{x}$ når sitt första maxvärde för $x=\frac{\pi}{2}$, så:
$$\frac{\pi}{{2}=(2k_{\text{optimal}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$$
Detta ger:
$$ {\text{k_optimal}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2=\frac{ \pi}{{4}\sqrt{\frac{N}{M}}--\frac{1}{2}O\left(\sqrt\frac{M}{N)}\right$$
Var i det sista steget, $\arccos \sqrt{1-x}=\sqrt{x} + O(x^{3/2}).$
Därför kan du välja $N_{\text{optimal}}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}–\frac{{1}{{2}\right\rgolv$.
Komplexitetsanalys
Från den tidigare analysen $behövs O\left(\sqrt{\frac{N}{M}}\right)$ frågor för oraklet $O_f$ för att hitta ett giltigt objekt. Men kan algoritmen implementeras effektivt när det gäller tidskomplexitet? $ $ O_0 baseras på databehandling av booleska åtgärder på $n$ bitar och är känd för att kunna implementeras med O$(n)$ grindar. Det finns också två lager av $n$ Hadamard-portar. Båda dessa komponenter kräver därför endast $O(n)$ portar per iteration. Eftersom $N=2^n$ följer $det O(n)=O(log(N))$. Om O(N M) iterationer och $O(log(N))\left-portar per iteration behövs är \sqrt{\frac{därför den totala tidskomplexiteten (utan att ta hänsyn till oracle-implementeringen) O}{(}}\rightN$M$log(N)$)$.\left\sqrt{\frac{}{}}\right$
Algoritmens övergripande komplexitet beror i slutändan på komplexiteten i implementeringen av oraklet $O_f$. Om en funktionsutvärdering är mycket mer komplicerad på en kvantdator än på en klassisk, blir den övergripande algoritmkörningen längre i kvantfallet, även om den tekniskt sett använder färre frågor.
Referenser
Om du vill fortsätta lära dig om Grover-algoritmen kan du kontrollera någon av följande källor:
- Originalpapper av Lov K. Grover
- Avsnittet kvantsökningsalgoritmer i Nielsen, M. A. &ere; Chuang, I. L. (2010). Kvantberäkning och kvantinformation.
- Grover-algoritmen på Arxiv.org