„DAG“ besteht nicht nur aus dem „A“
Veröffentlichung des Originalartikels: 16.09.2011
Definitionen
Wir alle wissen, dass DAG in der Welt von Microsoft Exchange für „Database Availability Group“ (Datenbankverfügbarkeitsgruppe) steht.
Datenbank: Wird verwendet, da auf einem hoch verfügbaren Postfachserver mit Exchange 2010 die Verfügbarkeit der Datenbank und nicht des Servers gemessen wird, und die Datenbank das Element ist, für das ein Failover oder eine Umschaltung zwischen mehreren Servern in einer DAG ausgeführt werden kann. Dieses Konzept wird als Datenbankmobilität bezeichnet.
Gruppe: Wird verwendet, da der Umfang der Verfügbarkeit durch Postfachserver in einer DAG bestimmt wird, die in einem Failovercluster kombiniert sind und als Gruppe zusammenarbeiten.
Verfügbarkeit: Dieses Wort scheint hier am wenigsten offensichtlich und am verwirrendsten zu sein (und außerdem im Bezug zu den beiden anderen Begriffen zu stehen). Ironischerweise hat das Wort eine eindeutige mathematische Definition und spielt eine wichtige Rolle beim Verständnis der allgemeinen Entwurfsprinzipien von Exchange.
In Wikipedia wird „Verfügbarkeit“ wie folgt definiert (sinngemäße Übersetzung des englischen Artikels):
- Das Maß, in dem sich ein System, Subsystem oder Gerät zu Beginn einer Aufgabe in einem vorgegebenen operativen und einsatzbereiten Zustand („committable“) befindet, wenn die Aufgabe zu einem unbekannten, das heißt zufälligen Zeitpunkt ausgeführt wird. Einfach ausgedrückt handelt es sich bei Verfügbarkeit um den Zeitanteil, in dem sich ein System in einem funktionsfähigen Zustand befindet. Dies wird häufig als Einsatzbereitschaftsrate („Mission Capable Rate“) bezeichnet. Mathematisch wird dies als 1 minus Nichtverfügbarkeit ausgedrückt.
- Das Verhältnis von (a) der Gesamtzeit, während der eine Funktionseinheit in einem bestimmten Intervall verwendet werden kann, zur (b) Dauer des Intervalls.
Beide Definitionen verwenden Begriffe aus der Wahrscheinlichkeitstheorie und bedeuten das Gleiche: die Wahrscheinlichkeit, dass ein bestimmtes System oder eine bestimmte Komponente zu jedem beliebigen Zeitpunkt (bei einem Test) „betriebsbereit“ ist oder „verwendet werden kann“ (das heißt verfügbar ist).
Mathematisch kann dies gemessen werden durch Berechnen der Zeit, während der das System über einen statistisch repräsentativen Zeitraum (in der Regel ein Jahr) verfügbar ist („Betriebszeit”), und Dividieren dieser Zeit durch die Gesamtdauer des Zeitraums. Anhand der allgemein verwendeten Begriffe mittlere Ausfallzeit zwischen Fehlern (Mean Time Between Failures, MTBF) und mittlere Reparaturzeit (Mean Time To Repair, MTTR) – der erste steht für die Systemverfügbarkeit bzw. -betriebszeit zwischen den Fehlern, der zweite hingegen für die Systemausfallzeit bei einem bestimmten Fehler – kann Verfügbarkeit als Bruch ausgedrückt werden:
Das mathematische Gegenteil wäre eine Fehlerwahrscheinlichkeit (denken Sie an „Nichtverfügbarkeit“):
Verfügbarkeit wird häufig gemäß der folgenden Tabelle als „Anzahl der Neunen” ausgedrückt:
Verfügbarkeitsstufe |
Verfügbarkeitswert |
Fehlerwahrscheinlichkeit |
Akzeptierte Ausfallzeit pro Jahr |
Zwei Neunen |
99 % |
1 % |
5256 Minuten = 3,65 Tage |
Drei Neunen |
99,9 % |
0,1 % |
525,6 Minuten = 8,76 Stunden |
Vier Neunen |
99,99 % |
0,01 % |
52,56 Minuten |
Fünf Neunen |
99,999 % |
0,001 % |
5,26 Minuten |
Natürlich unterscheidet sich der Verfügbarkeitswert je nachdem, ob wir geplante und nicht geplante Ausfallzeiten oder nur nicht geplante Ausfallzeiten berücksichtigen. Die Vereinbarung zum Servicelevel (Service Level Agreement, SLA), die Anforderungen für die geschäftliche Verfügbarkeit darstellt, muss in diesem Punkt sehr konkret sein. In jedem Fall hängt die Verfügbarkeit eines bestimmten Systems oder einer bestimmten Komponente jedoch von vielen Faktoren ab, und es ist unerlässlich, dass Sie diese Abhängigkeiten und ihre Auswirkungen auf die Verfügbarkeit identifizieren und verstehen.
Auswirkungen von Dienstabhängigkeiten auf die Verfügbarkeit
Die Verfügbarkeit einer Exchange-Postfachdatenbank hängt von der Verfügbarkeit vieler anderer Dienste und Komponenten ab – beispielweise von dem Speichersubsystem, auf dem die Datenbank gehostet wird, von dem Server, auf dem diese Datenbank betrieben wird, von der Netzwerkkonnektivität mit diesem Server usw. Alle diese Komponenten sind kritisch, und ein Fehler bei einer beliebigen einzelnen Komponente würde zum Verlust des Diensts führen, auch wenn die Datenbank selbst völlig fehlerfrei ist. Das heißt, damit die Datenbank als Dienst verfügbar ist, muss jede einzelne Abhängigkeit der Datenbank ebenfalls verfügbar sein. Wenn wir die Abhängigkeitskomponenten richtig identifizieren und isolieren, können wir mathematisch berechnen, wie diese die resultierende Verfügbarkeit der Exchange-Postfachdatenbank selbst bestimmen.
Für eine bestimmte Exchange-Postfachdatenbank können die folgenden Komponenten als kritische Abhängigkeiten betrachtet werden:
- Datenbankdatenträger/Speichersubsystem: Nehmen wir eine Verfügbarkeit von A1 an.
- Postfachserver (Hardware- und Softwarekomponenten): Nehmen wir eine Verfügbarkeit von A2 an.
- Clientzugriffsserver (Hardware- und Softwarekomponenten): Bedenken Sie, dass in Exchange 2010 alle Clients nur über den Clientzugriffsserver eine Verbindung mit der Postfachdatenbank herstellen. Nehmen wir an, der Clientzugriffsserver ist in diesem Fall getrennt vom Postfachserver installiert und hat eine Verfügbarkeit von A3.
- Netzwerkkonnektivität zwischen Clients und dem Clientzugriffsserver sowie zwischen dem Clientzugriffsserver und dem Postfachserver: Nehmen wir eine Verfügbarkeit von A4 an.
- Stromversorgung in dem Datencenter, in dem sich die Server und der Speicher befinden: Nehmen wir eine Verfügbarkeit von A5 an.
Diese Liste lässt sich fortsetzen … Beispielsweise stellen Active Directory und DNS ebenfalls kritische Abhängigkeiten für Exchange dar. Darüber hinaus wird die Verfügbarkeit nicht nur von rein technischen Abhängigkeiten, sondern auch von Prozessabhängigkeiten beeinflusst, beispielsweise von der Ausgereiftheit der Vorgänge usw.. So können menschliche Fehler, falsch definierte Vorgänge oder ein Mangel an Teamkoordination zu Dienstausfallzeiten führen. Wir wollen versuchen, hier keine erschöpfende Liste der Abhängigkeiten aufzustellen, sondern uns stattdessen auf deren Auswirkungen auf die allgemeine Dienstverfügbarkeit konzentrieren.
Da diese Komponenten selbst voneinander unabhängig sind, stellt die Verfügbarkeit jeder einzelnen Komponente ein unabhängiges Ereignis dar, und die resultierende Verfügbarkeit einer Exchange-Postfachdatenbank stellt eine Kombination aller dieser Ereignisse dar (mit anderen Worten: damit eine Postfachdatenbank für Clients verfügbar ist, müssen alle diese Komponenten verfügbar sein). Gemäß der Wahrscheinlichkeitstheorie ist die Wahrscheinlichkeit einer Kombination aus unabhängigen Ereignissen ein Produkt der Wahrscheinlichkeiten der einzelnen Ereignisse:
Wenn Sie beispielsweise drei Münzen werfen, beträgt die Wahrscheinlichkeit, dass alle drei Münzen mit dem Kopf nach oben landen, (1/2)*(1/2)*(1/2) = 1/8.
Es ist wichtig, zu erkennen, dass, da die einzelnen Verfügbarkeitswerte nicht größer als 1 (oder 100 %) sein können und die resultierende Dienstverfügbarkeit einfach ein Produkt einzelner Komponentenverfügbarkeiten ist, der resultierende Verfügbarkeitswert nicht größer sein kann als die niedrigste der abhängigen Komponentenverfügbarkeiten.
Dies kann anhand des Beispiels in der folgenden Tabelle veranschaulicht werden (bei den Zahlen handelt es sich um Beispiele, die jedoch recht realistisch sind):
Kritische Abhängigkeitskomponente |
Fehlerwahrscheinlichkeit |
Verfügbarkeitswert |
Postfachserver und Speicher |
5 % |
95 % |
Clientzugriffsserver |
1 % |
99 % |
Netzwerk |
0,5 % |
99,5 % |
Stromversorgung |
0,1 % |
99,9 % |
Allgemeiner Dienst (hängt von allen oben genannten Komponenten ab) |
6,51383 % |
95 % x 99 % x 99,5 % x 99,9 % = 93,48617 % |
An diesem Beispiel können Sie sehen, wie wichtig Dienstabhängigkeiten sind. Selbst für eine Postfachdatenbank, bei der nie Fehler auftreten (die nie beschädigt wird, nie mit einem Virus infiziert wird usw.), bleibt die Verfügbarkeit immer noch unter 93,5 %!
Schlussfolgerung: Eine große Anzahl von Dienstabhängigkeiten verringert die Verfügbarkeit.
Alles, was Sie tun können, um die Anzahl oder die Auswirkungen von Dienstabhängigkeiten zu verringern, wirkt sich positiv auf die allgemeine Dienstverfügbarkeit aus. Sie können beispielsweise die Ausgereiftheit der Vorgänge verbessern, indem Sie die Serververwaltung vereinfachen und sichern und betriebliche Verfahren optimieren. Auf der technischen Seite können Sie versuchen, die Anzahl der Dienstabhängigkeiten zu verringern, indem Sie den Entwurf vereinfachen, beispielsweise, indem Sie einen komplexen SAN-basierten Speicherentwurf mit HBA-Karten, Fiberswitches, Arraycontrollern und sogar RAID-Controllern eliminieren und ihn durch einen einfachen DAS-Entwurf mit einem Minimum an beweglichen Teilen ersetzen.
Die Verringerung der Dienstabhängigkeiten allein ist möglicherweise nicht ausreichend, um das gewünschte Maß an Verfügbarkeit zu erreichen. Bei einer anderen sehr effizienten Methode, die resultierende Verfügbarkeit zu erhöhen und die Auswirkungen kritischer Dienstabhängigkeiten zu minimieren, nutzen Sie verschiedene Redundanzmethoden nutzen, indem Sie beispielsweise doppelte Stromversorgungen und Netzwerkkartenteams verwenden, Server mit mehreren Netzwerkswitches verbinden, RAID-Schutz für das Betriebssystem verwenden und Lastenausgleich für Clientzugriffssserver sowie mehrere Kopien von Postfachdatenbanken bereitstellen. Aber auf genau welche Weise erhöht Redundanz die Verfügbarkeit? Werfen wir einen genaueren Blick auf den Lastenausgleich und auf mehrere Datenbankkopien als wichtige Beispiele.
Auswirkungen von Redundanz auf die Verfügbarkeit
Konzeptionell bedeuten alle Redundanzmethoden das Gleiche: Es gibt mehrere Instanzen der Komponente, die verfügbar ist und gleichzeitig mit anderen Instanzen (beim Lastenausgleich) oder als Ersatz (in mehreren Datenbankkopien) verwendet werden kann. Nehmen wir an, wir haben n Instanzen einer bestimmten Komponente (n Server in einem CAS-Array oder n Datenbankkopien in einer DAG). Selbst wenn bei einer Instanz ein Fehler auftritt, können die anderen Instanzen weiter verwendet werden, sodass die Verfügbarkeit aufrechterhalten wird. Die einzige Situation, in der es tatsächlich zu einer Ausfallzeit kommt, wäre ein Auftreten von Fehlern bei allen Instanzen.
Wie weiter oben definiert beträgt die Fehlerwahrscheinlichtkeit für eine bestimmte Instanz P = 1 – A. Alle Instanzen sind statistisch unabhängig voneinander, das heißt, die Verfügbarkeit einer Instanz oder ein Fehler bei einer Instanz wirkt sich nicht auf die Verfügbarkeit der anderen Instanzen aus. So wirkt sich beispielsweise ein Fehler bei einer bestimmten Datenbankkopie nicht auf die Fehlerwahrscheinlichkeit für eine andere Kopie dieser Datenbank aus (eine mögliche Ausnahme wäre die Beschädigung einer logischen Datenbank, die von der ersten beschädigten Datenbankkopie an alle weiteren Kopien verbreitet wird, diesen höchst unwahrscheinlichen Faktor ignorieren wir jedoch für den Moment – schließlich können Sie jederzeit eine isolierte Datenbankkopie oder eine herkömmliche Sicherung von einem bestimmten Zeitpunkt implementieren, um dieses Problem zu lösen).
Wenn wir wieder den gleichen Lehrsatz der Wahrscheinlichkeitstheorie verwenden, ist die Fehlerwahrscheinlichkeit für einen Satz von n unabhängigen Komponenten ein Produkt der Wahrscheinlichkeiten für die einzelnen Komponenten. Da hier alle Komponenten identisch sind (verschiedene Instanzen des gleichen Objekts), wird das Produkt zu einem Exponenten:
Da P < 1, ist Pn offensichtlich kleiner als P, das heißt, die Fehlerwahrscheinlichkeit nimmt ab, und die Verfügbarkeit steigt entsprechend:
Stellen wir uns zur Verdeutlichung ein Beispiel aus der Praxis vor. Wir stellen mehrere Kopien einer Postfachdatenbank bereit; jede Kopie wird auf einem einzigen SATA-Laufwerk gehostet. Statistisch beträgt die Fehlerrate von SATA-Laufwerken ~5 % pro Jahr[1], sodass sich eine Fehlerwahrscheinlichkeit von 5 % ergibt: P = 0,05 (das heißt eine Verfügbarkeit von 95 %: A = 0,95). Wie ändert sich die Verfügbarkeit, wenn wir mehr Datenbankkopien hinzufügen? Schauen Sie sich die folgende selbsterklärende Tabelle an:
Anzahl der Datenbankkopien |
Fehlerwahrscheinlichkeit |
Verfügbarkeitswert |
1 |
P1 = P = 5 % |
A1 = 1 – P1 = 95 % |
2 |
P2 = P2 = 0,25 % |
A2 = 1 – P2 = 99,75 % |
3 |
P3 = P3 = 0,125 % |
A3 = 1 – P3 = 99,9875 % |
4 |
P4 = P4 = 0,000625 % |
A4 = 1 – P4 = 99,9994 % |
Ziemlich beeindruckend, oder? Im Grund ergibt sich durch jede zusätzliche Datenbankkopie auf dem SATA-Laufwerk der Multiplikationsfaktor 5 % oder 1/20, sodass die Fehlerwahrscheinlichkeit mit jeder Kopie um das 20-Fache sinkt (und die Verfügbarkeit entsprechend steigt). Sie sehen, dass selbst mit den unzuverlässigsten SATA-Laufwerken durch die Bereitstellung von nur vier Datenbankkopien die Datenbankverfügbarkeit auf fünf Neunen steigt.
Das ist schon sehr gut, aber können Sie die Verfügbarkeit noch weiter verbessern? Können Sie die Verfügbarkeit weiter erhöhen, ohne Änderungen an der Architektur vorzunehmen (wenn beispielsweise das Hinzufügen einer weiteren Datenbankkopie nicht infrage kommt)?
Das ist tatsächlich möglich. Wenn Sie die einzelne Verfügbarkeit einer beliebigen Abhängigkeitskomponente verbessern, trägt dies zur Erhöhung der allgemeinen Dienstverfügbarkeit bei und führt dazu, dass sich das Hinzufügen redundanter Komponenten deutlich stärker auswirkt. Ohne umfangreiche Investitionen ist dies möglich, indem Sie Nearline-SAS-Laufwerke anstelle von SATA-Laufwerken verwenden. Nearline-SAS-Laufwerke haben eine jährliche Fehlerrate von ~2,75 % gegenüber ~5 % bei SATA-Laufwerken. Dadurch wird die Fehlerwahrscheinlichkeit für die Speicherkomponente in der oben gezeigten Berechnung verringert und daher die allgemeine Dienstverfügbarkeit erhöht. Vergleichen Sie die Auswirkungen durch Hinzufügen mehrere Datenbankkopien:
- 5 % AFR = Multiplikationsfaktor 1/20 = mit jeder neuen Kopie werden Datenbankfehler 20 Mal weniger wahrscheinlich.
- 2,75 % AFR = Multiplikationsfaktor 1/36 = mit jeder neuen Kopie werden Datenbankfehler 36 Mal weniger wahrscheinlich.
Diese signifikante Auswirkung zusätzlicher Datenbankkopien auf die Datenbankverfügbarkeit erklärt auch unsere Ratschläge zur Verwendung des systemeigenen Exchange-Datenschutzes, aus denen hervorgeht, dass mehrere Datenbankkopien als Ersatz für herkömmliche Sicherungen dienen können, wenn ausreichend viele (mindestens drei) Datenbankkopien bereitgestellt werden.
Die gleiche Logik gilt für die Bereitstellung mehrerer Clientzugriffsserver in einem CAS-Array, mehrerer Netzwerkswitches usw. Nehmen wir an, wir haben vier Datenbankkopien und vier Clientzugriffsserver bereitgestellt, und betrachten wir noch einmal die Komponentenverfügbarkeitstabelle, die wir weiter oben analysiert haben:
Kritische Abhängigkeitskomponente |
Fehlerwahrscheinlichkeit |
Verfügbarkeitswert |
Postfachserver und Speicher (vier Kopien) |
5 % ^ 4 = 0,000625 % |
99,999375 % |
Clientzugriffsserver (vier getrennt installierte Server) |
1 % ^ 4 = 0,000001 % |
99,999999 % |
Netzwerk |
0,5 % |
99,5 % |
Stromversorgung |
0,1 % |
99,9 % |
Allgemeiner Dienst (hängt von allen oben genannten Komponenten ab) |
0,6 % |
99,399878 % |
Sie können sehen, wie allein durch die Bereitstellung von vier Clientzugriffsservern und vier Datenbankkopien die Fehlerwahrscheinlichkeit für den allgemeinen Dienst um mehr als das 10-Fache (von 6,5 % auf 0,6 %) gesunken ist und die Dienstverfügbarkeit entsprechend von 93,5 % auf den erheblich besseren Wert 99,4 % gestiegen ist!
Schlussfolgerung: Durch Hinzufügen von Redundanz zu Dienstabhängigkeiten wird die Verfügbarkeit erhöht.
Wir fügen die Teile zusammen
Aus den bisherigen Schlussfolgerungen ergibt sich eine interessante Frage. Wir haben zwei verschiedene Faktoren analysiert, die sich in zweierlei Hinsicht auf die allgemeine Dienstverfügbarkeit auswirken, und haben zwei klare Schlussfolgerungen gezogen:
- Durch Hinzufügen weiterer Systemabhängigkeiten wird die Verfügbarkeit verringert.
- Durch Hinzufügen von Redundanz zu Systemabhängigkeiten wird die Verfügbarkeit erhöht.
Was geschieht, wenn beide Faktoren einer bestimmten Lösung sind? Welche Tendenz ist stärker?
Stellen Sie sich das folgende Szenario vor:
Wir stellen zwei Postfachserver in einer DAG mit zwei Kopien der Postfachdatenbank (eine Kopie auf jedem Server) bereit, und wir stellen zwei Clientzugriffsserver in einem Array mit Lastenausgleich bereit. (Der Einfachheit halber berücksichtigen wir nur die Verfügbarkeit einer Postfachdatenbank für Clientverbindungen und lassen Hub-Transport und Unified Messaging für den Moment unberücksichtigt). Nehmen wir an, jeder Server hat eine individuelle Fehlerwahrscheinlichkeit von P. Wird die Verfügbarkeit eines solchen Systems besser oder schlechter sein als die Verfügbarkeit eines einzigen eigenständigen Exchange-Servers, auf dem die Serverrollen Postfach und Clientzugriff bereitgestellt sind?
Im ersten Szenario sind die Postfachserver unabhängig und nur dann nicht verfügbar, wenn auf beiden Servern Fehler auftreten. Die Fehlerwahrscheinlichkeit für die beiden Postfachserver beträgt P × P = P2. Entsprechend beträgt die Verfügbarkeit AMBX = 1 – P2. Der gleichen Logik folgend sind die CAS-Dienste nur dann nicht verfügbar, wenn auf beiden Clientzugriffsservern Fehler auftreten, sodass die Fehlerwahrscheinlichkeit für beide Clientzugriffsserver wieder P × P = P2 beträgt. Entsprechend beträgt die Verfügbarkeit ACAS = 1 – P2.
Wie Sie möglicherweise erkannt haben, sind in diesem Fall zwei Postfachserver oder zwei Clientzugriffsserver Beispiele für redundante Systemkomponenten.
Bleiben wir bei diesem Szenario … Damit das gesamte System verfügbar ist, müssen beide Serversätze (der Satz der Postfachserver und der Satz der Clientzugriffsserver) gleichzeitig verfügbar sein. Es dürfen nicht auf beiden gleichzeitig Fehler auftreten, sondern beide müssen gleichzeitig verfügbar sein, da sie jetzt nicht redundante Komponenten, sondern Systemabhängigkeiten darstellen. Dies bedeutet, dass die allgemeine Dienstverfügbarkeit ein Produkt der Verfügbarkeiten der einzelnen Sätze ist:
Natürlich ist das zweite Szenario erheblich einfacher, da nur ein Server berücksichtigt werden muss, dessen Verfügbarkeit einfach A = 1 – P beträgt.
Nun haben wir die Verfügbarkeitswerte für beide Szenarien berechnet. Welcher Wert ist höher, (1-P2)2 oder 1-P?
Wenn wir die Diagramme beider Funktionen zeichnen, sehen wir folgendes Verhalten:
(Ich habe die Zeichnung schnell und einfach mit dem kostenlosen Berechnungsmodul Wolfram Alpha Mathematica Online erstellt.)
Wir können sehen, dass bei den kleinen Werten von P die Verfügbarkeit des komplexen Vier-Server-Systems höher ist als die Verfügbarkeit des einzelnen Servers. Das ist keine Überraschung, sondern entspricht unseren Erwartungen, richtig? Bei P ~ 0,618 (genauer 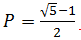 ) kreuzen sich die beiden Linien jedoch, und bei größeren Werten von P hat das System mit einem einzigen Server tatsächlich eine höhere Verfügbarkeit. Natürlich würden Sie erwarten, dass der Wert von P in der Praxis nahe Null ist; wenn Sie jedoch planen, eine Lösung aus sehr unzuverlässigen Komponenten zu erstellen, würden Sie mit einem einzigen Server vermutlich bessere Ergebnisse erzielen.
) kreuzen sich die beiden Linien jedoch, und bei größeren Werten von P hat das System mit einem einzigen Server tatsächlich eine höhere Verfügbarkeit. Natürlich würden Sie erwarten, dass der Wert von P in der Praxis nahe Null ist; wenn Sie jedoch planen, eine Lösung aus sehr unzuverlässigen Komponenten zu erstellen, würden Sie mit einem einzigen Server vermutlich bessere Ergebnisse erzielen.
Auswirkungen von Fehlerdomänen
Leider sind praktische Bereitstellungsszenarien selten so einfach wie die oben erörterten Situationen. Wie ändert sich beispielsweise die Dienstverfügbarkeit, wenn Sie Server mit mehreren Rollen bereitstellen? Wir haben in dem oben beschriebenen Szenario festgestellt, dass durch Kombinieren der Serverrollen die Anzahl der Dienstabhängigkeiten effektiv verringert wird – das wäre also wahrscheinlich gut, oder? Was geschieht, wenn Sie zwei Datenbankkopien der gleichen Datenbank auf dem gleichen SAN-Array oder im gleichen DAS-Gehäuse platzieren? Was ist, wenn alle Postfachserver mit dem gleichen Netzwerkswitch verbunden sind? Was ist, wenn nicht nur alle diese, sondern weitere Faktoren vorliegen?
In allen diesen Situationen spielt das Konzept der Fehlerdomänen eine Rolle. In den oben genannten Beispielen stellt die Serverhardware, ein SAN-Array oder ein Netzwerkswitch eine Fehlerdomäne dar. Die Fehlerdomäne beendet die Unabhängigkeit oder Redundanz der in der Fehlerdomäne kombinierten Komponenten. Beispielsweise bedeutet ein Fehler bei Serverhardware in einem Server mit mehreren Rollen, dass alle Exchange-Rollen auf diesem Server nicht mehr verfügbar sind; entsprechend bedeutet ein Fehler bei einem Datenträgergehäuse oder einem SAN-Array, dass alle in diesem Gehäuse oder Array gehosteten Datenbankkopien nicht mehr verfügbar sind.
Fehlerdomänen sind nicht zwangsläufig etwas Negatives. Entscheidend ist, aus welchen Arten von Komponenten eine Fehlerdomäne besteht: Handelt es sich um verschiedene Systemabhängigkeiten oder um redundante Systemkomponenten? Betrachten wir zwei der oben genannten Beispiele, um uns den Unterschied klarzumachen.
Szenario mit Server mit mehreren Rollen
Vergleichen wir die Verfügbarkeit der zwei verschiedenen Systeme:
- Die Serverrollen Postfach und Clientzugriff werden auf dem gleichen Server gehostet, für den die Wahrscheinlichkeit eines Hardwarefehlers P beträgt.
- Die gleichen Rollen werden auf zwei getrennten Servern gehostet, die beide die gleiche Wahrscheinlichkeit eines Hardwarefehlers haben.
Im ersten Fall stellt die Hardware eines einzelnen Servers eine Fehlerdomäne dar. Dies bedeutet, dass entweder alle gehosteten Rollen verfügbar sind oder dass alle gehosteten Rollen nicht verfügbar sind. Dies ist einfach; die allgemeine Verfügbarkeit eines solchen Systems beträgt A = 1 – P.
Im zweiten Fall ist der allgemeine Dienst nur verfügbar, wenn beide Server unabhängig voneinander verfügbar sind (da jede Rolle eine kritische Abhängigkeit darstellt). Auf der Wahrscheinlichkeitstheorie basierend beträgt daher die Verfügbarkeit A × A = A2.
Auch hier ist A < 1, das heißt, A2 < A, also ist im zweiten Fall die Verfügbarkeit niedriger.
Offensichtlich können wir im gleichen Szenario weitere Exchange-Serverrollen (Hub-Transport und gegebenenfalls Unified Messaging) hinzufügen, ohne gegen diese Logik zu verstoßen.
Schlussfolgerung: Durch die Kollokation von Exchange-Serverrollen auf einem Server mit mehreren Rollen wird die allgemeine Dienstverfügbarkeit erhöht.
Szenario mit freigegebenem Speicher
Betrachten wir nun ein weiteres Fehlerdomänenszenario (zwei Datenbankkopien im gleichen Speicherarray), und vergleichen wir die Datenbankverfügbarkeit in den beiden folgenden Fällen:
- Zwei Datenbankkopien werden im gleichen freigegebenen Speicher (SAN-Array oder DAS-Gehäuse) gehostet, das die Fehlerwahrscheinlichkeit P hat.
- Die gleichen Datenbankkopien werden in zwei getrennten Speichersystemen gehostet, die beide die gleiche Fehlerwahrscheinlichkeit haben.
Im ersten Fall stellt der freigegebene Speicher eine Fehlerdomäne dar. Wie im vorherigen Szenario bedeutet dies, dass beide Datenbankkopien gleichzeitig verfügbar oder nicht verfügbar sind. Daher beträgt die allgemeine Verfügbarkeit wieder A = 1 – P.
Im zweiten Fall ist der allgemeine Dienst verfügbar, wenn mindestens ein System verfügbar ist, bzw. nicht verfügbar, wenn bei beiden Systemen Fehler auftreten. Die jeweiligen Speichersysteme sind unabhängig; daher beträgt die Fehlerwahrscheinlichkeit für den allgemeinen Dienst P × P = P2, und die allgemeine Dienstverfügbarkeit beträgt entsprechend A = 1 – P2.
Auch hier ist P < 1, das heißt P2 < P, und daher ist 1 – P2 > 1 – P. Dies bedeutet, dass im zweiten Fall die Verfügbarkeit höher ist.
Schlussfolgerung: Durch Kollokation von Datenbankkopien im gleichen Speichersystem wird die allgemeine Dienstverfügbarkeit verringert.
Was ist also der Unterschied zwischen diesen beiden Szenarien? Wieso wird durch Hinzufügen einer Fehlerdomäne die Verfügbarkeit im ersten Fall erhöht und im zweiten Fall verringert?
Der Grund ist, dass die Fehlerdomäne im ersten Fall Dienstabhängigkeiten kombiniert und damit effektiv deren Anzahl verringert und dadurch die Verfügbarkeit verbessert, während die Fehlerdomäne im zweiten Fall redundante Komponenten kombiniert und damit effektiv die Redundanz verringert und dadurch die Verfügbarkeit beeinträchtigt.
Alle diese Konzepte und Schlussfolgerungen können vermutlich wie folgt visualisiert werden:
(Nein, dieses Diagramm wurde nicht mit Wolfram Alpha gezeichnet!)
Zusammenfassung
Die Architektur von Exchange 2010 bietet vielversprechende Möglichkeiten zum Hinzufügen von Redundanz auf Exchange-Ebene (beispielsweise durch Bereitstellen mehrerer Datenbankkopien oder mehrerer Clientzugriffsserver in einem CAS-Array) und zum Verringern der Anzahl der Systemabhängigkeiten (durch Kombinieren von Exchange-Serverrollen auf einem Server mit mehreren Rollen oder durch Verwenden einer einfacheren Speicherarchitektur ohne übermäßig viele kritische Komponenten). Anhand der in diesem Artikel vorgestellten einfachen Regeln und Formeln können Sie die Auswirkung der Bereitstellung zusätzlicher Datenbankkopien oder der Kombination von Exchange-Serverrollen auf den Verfügbarkeitswert berechnen; außerdem können Sie die Auswirkungen von Fehlerdomänen berechnen. Dabei ist zu beachten, dass wir versucht haben, diese einfachen mathematischen Modelle zur Veranschaulichung der Konzepte zu verwenden, und nicht um vorgeblich präzise Verfügbarkeitswerte zu erhalten. Die Praxis entspricht selten den einfachen Basisszenarien, und Sie benötigen deutlich komplexere Berechnungen, um realistische Schätzungen für die Verfügbarkeit Ihrer tatsächlichen Systeme zu erhalten; möglicherweise ist es einfacher, lediglich die Verfügbarkeit statistisch zu messen und zu überprüfen, ob sie den SLA-Anforderungen entspricht. Wenn Sie die Faktoren kennen, die sich auf die Verfügbarkeit auswirken, und verstehen, wie diese in einer komplexen Entwicklungslösung zusammenwirken, sollte Ihnen dies helfen, die Lösung richtig zu entwerfen und eine signifikante Steigerung der allgemeinen Dienstverfügbarkeit zu erzielen, die auch den anspruchsvollsten geschäftlichen Anforderungen entspricht.
Boris Lokhvitsky
Delivery Architect
[1] Aus den folgenden Studien der Carnegie Mellon University, von Google und von Microsoft Research geht für SATA-Laufwerke eine jährliche Fehlerrate (Annual Failure Rate, AFR) von 5 % hervor:
https://www.usenix.org/events/fast07/tech/schroeder/schroeder.pdf
https://labs.google.com/papers/disk_failures.pdf
https://research.microsoft.com/research/pubs/view.aspx?msr_tr_id=MSR-TR-2005-166
Es handelt sich hierbei um einen übersetzten Blogbeitrag. Sie finden den Originalartikel unter DAG: Beyond the “A”.








