Поделиться через

Кривые параметров

  • Статья

Параметры мультимедиа могут следовать кривой с течением времени. Каждая кривая описывается математической формулой и двумя конечными точками. Каждая конечная точка определяется по времени ссылки и значению кривой в это время. Формула используется для вычисления промежуточных значений между точками и определяет форму кривой. Возможные кривые:

  • Прыгать
  • Линейная
  • Square
  • Обратный квадрат
  • Синус

"Переход" означает переход непосредственно к конечному значению. Другие кривые показаны на следующей схеме.

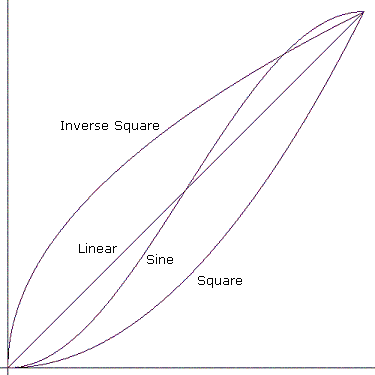
parameter curves

Математически кривые работают следующим образом. Предположим, что кривая начинается во время t₀ со значением v₀ и заканчивается во время t₁ значением v₁. Двумя точками, определяющими кривую, являются (t₀, v₀) и (t₁, v₁).

  • Пусть ₀ будет общей продолжительностью кривой, t₁–t₀.
  • Позвольте TM быть интервалом между начальными и конечными значениями , v₁–v₀.
  • В любое время не так, чтобы t₀ <=<t= t₁, пусть ₁ =t–t₀.

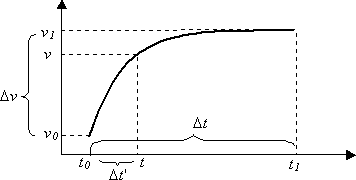
parameter calculation

Значение параметра во время t :

v = f( Δt' / Δt ) * TMv + ₀

где f(x) — это функция, определяемая типом кривой:

  • Линейный: y = x
  • Квадрат: y = x^2
  • Обратный квадрат: y = sqrt(x)
  • Синус: y = [ sin(πx – π/2) + 1 ] / 2

Обратите внимание на то,что TM'< TM, поэтому термин Δt'/Δt колеблется от 0 до 1. Таким образом, f(x) также диапазоны от 0 до 1, а v всегда падает между v₀ и v₁. Это верно: v₀ <v₁ или наоборот. Другими словами, кривая ограничена прямоугольником (t₀, v₀, t₁, v₁).

Для кривой синуса значение (πx – π/2) колеблется от –π/2 до π/2, что означает, что грех(πx – π/2) колеблется от –1 до 1. Затем результат нормализуется, чтобы f(x) попал в диапазон (0–1).

Параметры мультимедиа