Алгоритм вектора ориентации устройства
В этой статье описывается алгоритм, который используется комплектом аппаратной лаборатории Windows (Windows HLK) для определения разницы между полученным и ожидаемым вектором для точности 9-осных данных в расширенных тестах датчика ориентации. Тесты проверяют правильность интеграции датчиков, а также правильность интеграции и установки всех датчиков, необходимых для слияния датчиков.
Примечание
В некоторых случаях средство диагностики датчика можно использовать для проверки трехмерного инклинометра и агрегированного датчика ориентации устройства, который тестируется.
Алгоритм вектора кватерниона
Алгоритм использует дуговой cos 4-мерного точечного произведения двух векторов, разделенный на произведение величины двух векторов и разделенный на 2. Этот алгоритм показан на рис. 1. Формула алгоритма вектора кватерниона:
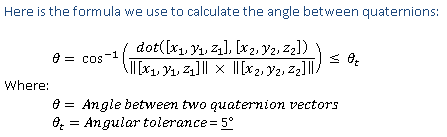
Значения матрицы поворота преобразуются в значения кватернионов для проверки точности. Вычисляемый вектор кватерниона должен отклоняться не более чем на +/- 5 градусов от ожидаемого вектора кватерниона (погрешность по сравнению с углом, сформированным между векторами кватернионов) (точность **+/- 10 градусов, допустимая для направления оси направления). Тест Windows HLK позволяет, чтобы дельта Øt была до 15 градусов.
Вычисление угла дельты между полученным и ожидаемым векторами кватерниона
В этом разделе описывается вычисление, при котором вычисляется разностный угол между полученным и ожидаемым векторами кватерниона в расширенных тестах ориентации в HLK Windows.
Следующие два значения данных представляют интерес для отчета об агрегированном датчике ориентации устройства:
Вектор кватерниона
Матрица поворота
Тест состоит из следующих двух проверок:
Проверка полученного вектора кватерниона в отчете о данных датчика. Вектор кватерниона имеет вид (xi + yj + zk + w).
Значение w всегда должно быть положительным.
Ожидается, что вектор кватерниона будет нормализованным и ненулевым. Например, величина вектора должна быть близка к 1,0. Один процент (1%) предоставляется для округления ошибок при вычислении величины.
Дельта-угол вычисляется с помощью delta = 2 * Acos( ( Exp . Rec ) / ( | Exp | * | Rec | ) ), где:
\* указывает скалярное умножение
. указывает точечный продукт
Exp — это ожидаемый вектор Quternion.
Rec — это полученный вектор кватерниона.
| Вопрос |указывает величину вектора квтерниона.
delta — это угол в градусах
Если значение delta больше 360 градусов, delta вычисляется как delta = delta - 360.
На этом этапе значение delta должно быть меньше или равно допустимому значению погрешности; например, 10 градусов.
Проверка полученной матрицы поворота. Ожидается, что матрица поворота будет матрицей 3x3.
Каждый столбец и вектор строки матрицы поворота должен быть нормализованным и ненулевым. Для округления ошибок при вычислении величины предоставляется 1 процент (1).
Полученная матрица поворота преобразуется в вектор кватерниона.
Все шаги от <> до <e> проверки (1) используются повторно.
Связанные темы
Тестирование функциональных возможностей датчика с помощью средства диагностики датчиков