Глубокое обучение

Завершено

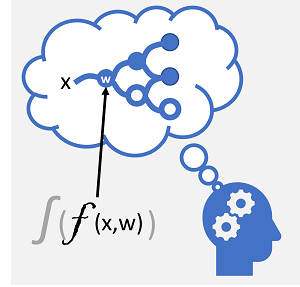
Глубокое обучение — это сложная форма машинного обучения, которая имитирует то, как учится мозг человека. Ключом к глубокому обучению является создание искусственной нейронной сети , которая имитирует электрохимическую активность в биологических нейронах с помощью математических функций, как показано здесь.

Биологическая нейронная сеть	Искусственная нейронная сеть
Нейроны запускают в ответ на электрохимические стимулы. При срабатывании сигнал передается подключенным нейронам.	Каждый нейрон является функцией, которая работает с входным значением (x) и весом (w). Функция заключена в функцию активации , которая определяет, следует ли передавать выходные данные.

Искусственные нейронные сети состоят из нескольких слоев нейронов, по существу определяющих глубоко вложенные функции. Эта архитектура является причиной, по которой метод называется глубоким обучением , а модели, созданные ею, часто называются глубокими нейронными сетями (DN). Глубокие нейронные сети можно использовать для многих видов задач машинного обучения, включая регрессию и классификацию, а также более специализированные модели для обработки естественного языка и компьютерного зрения.

Как и другие методы машинного обучения, обсуждаемые в этом модуле, глубокое обучение включает в себя установку обучающих данных в функцию, которая может прогнозировать метку (y) на основе значения одного или нескольких признаков (x). Функция (f(x)) — это внешний слой вложенной функции, в котором каждый слой нейронной сети инкапсулирует функции, работающие с x и связанными с ними значениями веса (w). Алгоритм, используемый для обучения модели, включает итеративную передачу значений признаков (x) в обучающие данные вперед через слои для вычисления выходных значений для ŷ, проверку модели для оценки того, насколько далеко от вычисляемых значений ŷ находятся от известных значений y (что определяет уровень погрешности или потери в модели). а затем измените весовые коэффициенты (w), чтобы уменьшить потери. Обученная модель включает конечные значения веса, которые приводят к наиболее точным прогнозам.

Пример. Использование глубокого обучения для классификации

Чтобы лучше понять, как работает модель глубокой нейронной сети, давайте рассмотрим пример, в котором нейронная сеть используется для определения модели классификации для видов пингвинов.

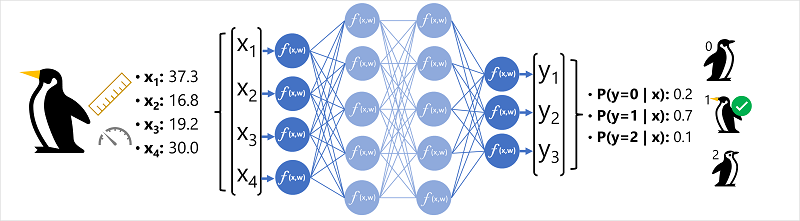
Данные признака (x) состоят из некоторых измерений пингвина. В частности, это следующие измерения:

• длина клюва пингвина;
• высота клюва пингвина;
• Длина ласт пингвина.
• вес пингвина.

В этом случае x является вектором четырех значений или математически x=[x1,x2;x3;x4].

Метка, которую мы пытаемся предсказать (y), это вид пингвина, и что есть три возможных вида это может быть:

• Adelie
• Папуанский
• Антарктический

Это пример задачи классификации, в которой модель машинного обучения должна прогнозировать наиболее вероятный класс, к которому относится наблюдение. Модель классификации делает это путем прогнозирования метки, состоящей из вероятности для каждого класса. Другими словами, y является вектором трех значений вероятности; по одному для каждого из возможных классов: [P(y=0|x), P(y=1|x), P(y=2|x)].

Процесс вывода прогнозируемого класса пингвинов с помощью этой сети:

1. Вектор признаков для наблюдения за пингвином подается во входной слой нейронной сети, который состоит из нейрона для каждого значения X . В этом примере в качестве входных данных используется следующий вектор x : [37.3, 16.8, 19.2, 30.0]
2. Функции для первого слоя нейронов вычисляют взвешиваемую сумму, объединяя значение x и вес w , и передают ее в функцию активации, которая определяет, соответствует ли она порогу для передачи следующему слою.
3. Каждый нейрон в слое соединен со всеми нейронами в следующем слое (архитектура иногда называется полностью подключенной сетью), поэтому результаты каждого слоя передаются вперед по сети, пока они не достигнут выходного слоя.
4. Выходной слой создает вектор значений; в этом случае с помощью функции softmax или аналогичной для вычисления распределения вероятности для трех возможных классов пингвинов. В этом примере выходной вектор: [0.2, 0.7, 0.1]
5. Элементы вектора представляют вероятности для классов 0, 1 и 2. Второе значение является самым высоким, поэтому модель прогнозирует, что вид пингвина равен 1 (Gentoo).

Как учится нейронная сеть?

Весовые коэффициенты в нейронной сети являются ключевыми для вычисления прогнозируемых значений для меток. В процессе обучения модель изучает весовые коэффициенты , которые позволят получить наиболее точные прогнозы. Давайте рассмотрим процесс обучения более подробно, чтобы понять, как происходит это обучение.

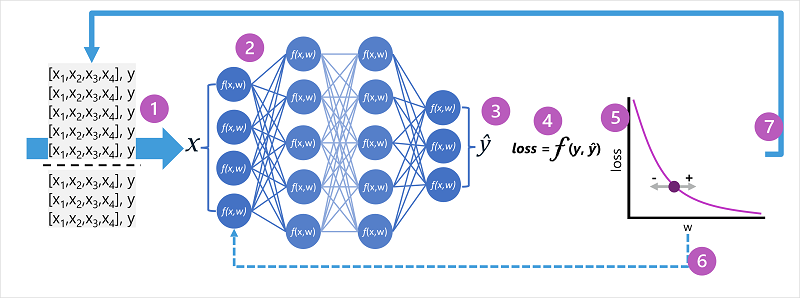
1. Наборы данных для обучения и проверки определяются, а функции обучения передаются на уровень входных данных.
2. Нейроны в каждом слое сети применяют свои весовые коэффициенты (которые изначально назначаются случайным образом) и передают данные через сеть.
3. Выходной слой создает вектор, содержащий вычисляемые значения для ŷ. Например, выходные данные для прогноза класса пингвина могут быть [0,3. 0.1. 0.6].
4. Функция потерь используется для сравнения прогнозируемых значений ŷ с известными значениями y и агрегирования разницы (которая называется потерей). Например, если известным классом для варианта, возвращающего выходные данные на предыдущем шаге, является Chinstrap, то значение y должно быть [0,0, 0,0, 1,0]. Абсолютная разница между этим и вектором ŷ составляет [0,3, 0,1, 0,4]. На самом деле функция потерь вычисляет агрегатную дисперсию для нескольких случаев и суммирует ее в виде одного значения потерь .
5. Так как вся сеть по сути является одной большой вложенной функцией, функция оптимизации может использовать дифференциальное вычисление для оценки влияния каждого веса в сети на потери и определения того, как их можно скорректировать (вверх или вниз) для уменьшения общей потери. Конкретный метод оптимизации может отличаться, но обычно включает в себя градиентный спуск , при котором каждый вес увеличивается или уменьшается, чтобы свести к минимуму потери.
6. Изменения весов возвращаются к слоям в сети, заменяя ранее использованные значения.
7. Этот процесс повторяется в нескольких итерациях (известных как эпохи), пока потери не будут сведены к минимуму и модель не будет прогнозироваться приемлемо точно.

Примечание

Хотя проще представить каждый случай в обучающих данных, передаваемых по сети по одному, на самом деле данные объединяются в матрицы и обрабатываются с помощью линейных алгебраических вычислений. По этой причине обучение нейронной сети лучше всего выполнять на компьютерах с графическими процессорами (GPU), оптимизированными для векторных и матричных операций.