Классификация по нескольким классам
Многоклассовая классификация используется для прогнозирования того, к каким из нескольких возможных классов относится наблюдение. В качестве защищенной техники машинного обучения он следует тому же итеративному обучению, проверке и оценке процесса как регрессии и двоичной классификации, в которой подмножество обучающих данных хранится обратно для проверки обученной модели.
Пример : многоклассовая классификация
Алгоритмы многоклассовой классификации используются для вычисления значений вероятности для нескольких меток классов, что позволяет модели прогнозировать наиболее вероятный класс для данного наблюдения.
Давайте рассмотрим пример, в котором у нас есть некоторые наблюдения за пингвинами, в которых длина листы (x) каждого пингвина записана. Для каждого наблюдения данные включают виды пингвинов (y), которые кодируются следующим образом:
- 0: Adelie
- 1: Дженту
- 2: Chinstrap
Примечание.
Как и в предыдущих примерах этого модуля, реальный сценарий будет включать несколько значений функции (x). Мы будем использовать одну функцию для простоты.
 |
 |
|---|---|
| Длина флиппера (x) | Виды (y) |
| 167 | 0 |
| 172 | 0 |
| 225 | 2 |
| 197 | 1 |
| 189 | 1 |
| 232 | 2 |
| 158 | 0 |
Обучение модели многоклассовой классификации
Чтобы обучить модель многоклассовой классификации, необходимо использовать алгоритм для соответствия обучающих данных функции, которая вычисляет значение вероятности для каждого возможного класса. Для этого можно использовать два типа алгоритма:
- Алгоритмы one-vs-Rest (OvR)
- Многономические алгоритмы
Алгоритмы one-vs-Rest (OvR)
Алгоритмы one-vs-Rest обучают двоичную функцию классификации для каждого класса, каждый вычисляет вероятность того, что наблюдение является примером целевого класса. Каждая функция вычисляет вероятность того, что наблюдение является определенным классом по сравнению с любым другим классом. Для модели классификации видов пингвинов алгоритм фактически создаст три функции двоичной классификации:
- f0(x) = P(y=0 | x)
- f1(x) = P(y=1 | x)
- f2(x) = P(y=2 | x)
Каждый алгоритм создает сигмоидную функцию, которая вычисляет значение вероятности от 0,0 до 1.0. Модель, обученная с помощью этого типа алгоритма, прогнозирует класс для функции, которая создает выходные данные наибольшей вероятности.
Многономические алгоритмы
В качестве альтернативного подхода используется многономичный алгоритм, который создает одну функцию, которая возвращает многозначные выходные данные. Выходные данные — это вектор (массив значений), который содержит распределение вероятностей для всех возможных классов — с оценкой вероятности для каждого класса, который при итоговом размере до 1,0:
f(x) =[P(y=0|x), P(y=1|x), P(y=2|x)]
Примером такой функции является функция softmax , которая может создать выходные данные, как показано в следующем примере:
[0.2, 0.3, 0.5]
Элементы в векторе представляют вероятности для классов 0, 1 и 2 соответственно; поэтому в этом случае класс с наибольшей вероятностью равен 2.
Независимо от того, какой тип алгоритма используется, модель использует результирующую функцию для определения наиболее вероятного класса для заданного набора функций (x) и прогнозирует соответствующую метку класса (y).
Оценка модели многоклассовой классификации
Вы можете оценить многоклассовый классификатор, вычисляя метрики двоичной классификации для каждого отдельного класса. Кроме того, можно вычислить статистические метрики, которые учитывают все классы.
Предположим, что мы проверили наш многоклассовый классификатор и получили следующие результаты:
| Длина флиппера (x) | Фактические виды (y) | Прогнозируемые виды (ŷ) |
|---|---|---|
| 165 | 0 | 0 |
| 171 | 0 | 0 |
| 205 | 2 | 1 |
| 195 | 1 | 1 |
| 183 | 1 | 1 |
| 221 | 2 | 2 |
| 214 | 2 | 2 |
Матрица путаницы для многоклассового классификатора похожа на матрицу двоичного классификатора, за исключением того, что она показывает количество прогнозов для каждого сочетания прогнозируемых (ŷ) и фактических меток классов (y):
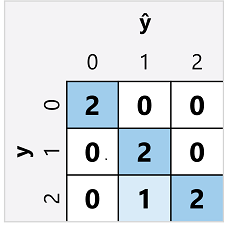
В этой матрице путаницы можно определить метрики для каждого отдельного класса следующим образом:
| Класс | ИП | ИО | FP | ЛО | Правильность | Отзыв | Точность | F1-Score |
|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 5 | 0 | 0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 1 | 2 | 4 | 1 | 0 | 0,86 | 1.0 | 0.67 | 0,8 |
| 2 | 2 | 4 | 0 | 1 | 0,86 | 0.67 | 1.0 | 0,8 |
Чтобы вычислить общую точность, отзыв и метрики точности, используйте общую сумму метрик TP, TN, FP и FN:
- Общая точность = (13+6)÷(13+6+1+1) = 0,90
- Общий отзыв = 6÷(6+1) = 0,86
- Общая точность = 6÷(6+1) = 0,86
Общая оценка F1 вычисляется с использованием общих метрик отзыва и точности:
- Общая оценка F1 = (2x0.86x0.86)÷(0,86+0,86) = 0,86