Что такое суперпозиция в квантовых вычислениях?
Если кот из предыдущей единицы был квантовым котом, состояние квантовой кошки и системы коробки будет одинаково: сумма шести различных позиций квантовой кошки относительно коробки, взвешаемая вероятностью поиска квантовой кошки в этой позиции. Единственное различие заключается в том, что классический кот может находиться в одном (и только один) из шести возможных позиций, в то время как квантовый кот может находиться во всех шести позициях одновременно!
В классическом мире объекты могут находиться только в одном состоянии одновременно. Однако в квантовом мире квантовые частицы могут находиться в нескольких состояниях одновременно. Это явление называется суперпозицией.
В квантовых вычислениях никто не использует квантовых кошек - к сожалению - но кубитов. Слово "кубит" означает "квантовый бит". Как и в классических вычислениях, где основная единица информации является битом, в квантовых вычислениях базовая единица информации является кубитом. И так же, как бит может принимать два возможных значения, 0 и 1, кубит является любой квантовой частицей, которая может быть в двух возможных состояниях. Например, кубит может быть фотоном, который может быть поляризован в двух направлениях, или электрон, который может находиться на двух уровнях энергии.
Как можно представить суперпозицию в кубите? Какова вероятность поиска кубита в определенном состоянии?
Как можно представить суперпозицию в кубите?
Кубит — это квантовая частица с двумя возможными позициями или состояниями. Как аналог классического бита, квантовые состояния кубита также называются $0$ и $1$. Кубит может находиться в штате $ 0$, в штате $ 1$, и в любом суперпозиции обоих штатов. Как вы можете представить эту суперпозицию?
Представьте, что вы рисуете круг и вертикальную и горизонтальную оси, чтобы средняя точка была центром круга. Состояние $0$ помещается в верхнюю точку вертикальной оси, а состояние $ 1$ находится в нижней точке.
Как можно описать это представление? Можно сказать, что состояние $0$ является стрелкой или вектором, указывая вверх и состояние $1$ является вектором, указывающим вниз. Поэтому классический бит будет вектором, указывающим либо вверх, либо вниз, но никогда не в другом направлении.
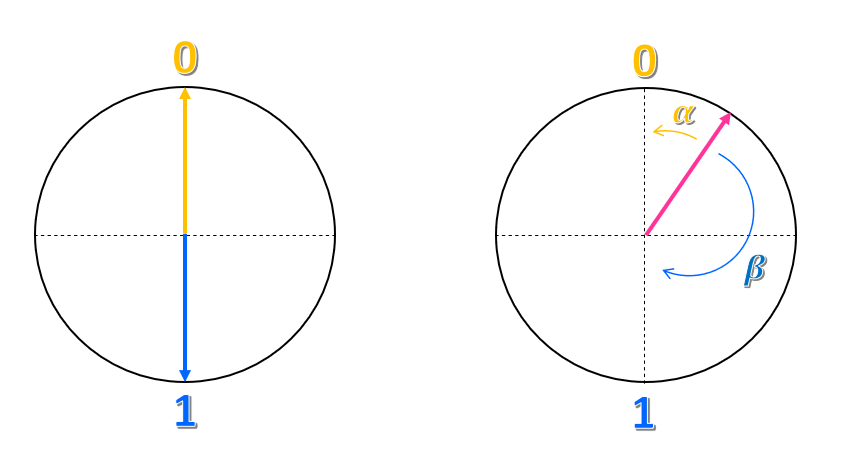
Что насчет любой другой точки круга? Как вы можете представить это состояние? Так же, как координаты в плоскости, вы можете попытаться представить его как сочетание двух состояний $ 0$ и $ 1$. Например, можно взять, как закрыть вектор от состояния $0$ и вызвать этот угол $\alpha$, и как близко от состояния $ 1$ и вызвать этот угол $\beta$. Мы могли бы представить состояние как $\alpha 0 + \beta 1 $. Таким образом, государство является суперпозицией штатов $ 0$ и $ 1$.
Как и пример кота и коробки, глобальное состояние кубита — сумма отдельных состояний, $0$ и $1$, взвешенная вероятностью поиска кубита в этом состоянии, $\alpha$ и $\beta $.
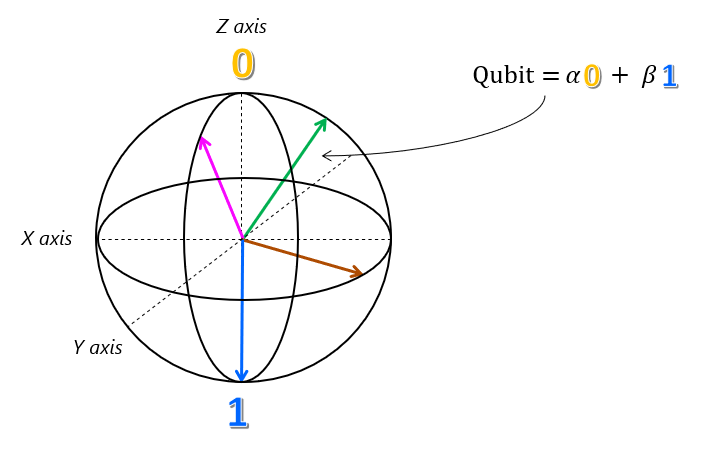
Это представление кубита на самом деле является точным, и оно называется сферой Blockh.
Совет
Область Blockh является мощным инструментом, так как операции, которые мы можем выполнять на кубите, можно представить как повороты одного из кардиналов. Рассмотрение квантовых вычислений как последовательности поворотов является многообещающей догадкой, однако эту догадку сложно применить в разработке и описании алгоритмов. Q# устраняет эту проблему, предоставляя язык для описания таких поворотов.
Какова вероятность поиска кубита в состоянии?
Как и в примере кота и коробки предыдущего урока, глобальное состояние кубита — это сумма отдельных состояний, $0$ и $1$, взвешенная вероятностью поиска кубита в этом состоянии, $\alpha$ и $\beta $. Цифры $\alpha$ и $\beta$ представляют, как "закрыть" состояние кубита в состояниях $0$ и $1$соответственно. Итак, являются ли $\alpha$ и $\beta$ вероятность поиска кубита в состоянии $0$ или $1$? Не совсем.
Числа $\alpha$ и $\beta$ являются амплитудами вероятности для каждого состояния. Их абсолютные значения, например $|\alpha|^2$ дают соответствующие вероятности. Например, вероятность наблюдения за состоянием $0$ составляет $|\alpha|^2$, а вероятность наблюдения за состоянием $1$ составляет $|\beta|^2$.
Числа $\alpha$ и $\beta$ могут быть положительными, отрицательными или даже сложными числами. Однако в допустимой квантовой суперпозиции все вероятности должны суммироваться до одного: $|\alpha|^2+|\beta|^2=1$. Это ограничение называется условием нормализации. Условие нормализации говорит о том, что при измерении вы всегда получите результат. Поэтому полная вероятность измерения каждого возможного результата равна единице.