Как использовать запутанность для отправки информации?
В предыдущих уроках вы узнали, что квантовое запутание может быть отличным ресурсом для квантового взаимодействия. В этом уроке вы увидите одно из самых известных приложений запутания: протокол квантового телепортации.
В телепортации запутанность используется для передачи состояния кубита из одного расположения в другое. Состояние кубита передается другому кубите, но сам кубит не перемещается физически. Это важно помнить! Сведения о состоянии кубита передаются другому кубитом, который используется в качестве судна для записи сведений о кубите сообщения.
Протокол телепортации использует сочетание запутанности и классической связи. Классическая связь важна, так как протокол телепортации требует от отправителя передачи результатов их измерений получателю. Это означает, что телепортация не может отправлять информацию быстрее, чем скорость света. Классическая связь между отправителем и получателем ограничена скоростью света.
Давайте рассмотрим протокол квантовой телепортации.
Протокол квантовой телепортации
Алиса и Боб работают вместе в одной компании. Алиса базируется в Сиэтле, и Боб базируется в Лос-Анджелесе. Они работают над проектом, который требует от них совместного использования квантовых сведений. Они решили использовать квантовую телепортацию для отправки квантовых данных между ними.
Начальная настройка
Алиса и Боб каждый имеют кубит, который является частью запутанных пар, которые ранее были подготовлены. Запутанные пары — это состояние Колокола, которое является состоянием
$$\ket{\phi}=\frac1{\sqrt2}(\ket{0_A 0_B + \ket{1_A 1_B}})$$
Алиса имеет дополнительный кубит , называемый "кубитом сообщения" - и хочет отправить этот кубит Бобу. Кубит сообщения находится в неизвестном состоянии, что Алиса хочет телепортировать Бобу. Состояние кубита сообщения
$$\ket{m}=\alpha\ket{{0}_m + \beta\ket{{1}_m,$$
где $\alpha$ и $\beta$ являются сложными числами.
Глобальное состояние Алисы и трех кубитов Боба
$$\ket{\text{Global}} (_m + \beta\ket{1}_m)\frac\otimes 1{\sqrt2}(\alpha\ket{\ket{{0}0_A 0_B+ \ket{1_A 1_B}})=$$
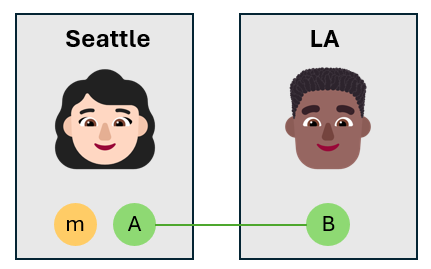
Алиса запутает кубитов сообщение с ее собственным кубитом
Алиса принимает кубит сообщения и запутает его с ее собственным кубитом $A$ с помощью ворот CNOT. Кубит сообщения является кубитом элемента управления, и кубит Алисы является target кубитом. Это создает трехкубитное запутанное состояние.
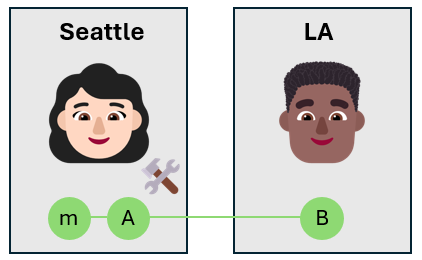
Кубит сообщения находится в неизвестном состоянии $\alpha\ket{0}_m + \beta\ket{1}_m$, поэтому после применения ворот CNOT, кубиты Алисы находятся в суперпозиции четырех состояний Bell. Глобальное состояние трех кубитов
$$\ket{\text{Global}}\frac=1\ket{\phi{{2}^+}_\text{mA} ({0}\alpha\ket{_B + \beta\ket{{1}_B) +$$
$$+ \frac1{2}\ket{\phi{^-}_\text{mA} (\alpha\ket{0}_B - \beta\ket{1}_B) +$$
$$+ \frac1{2}\ket{\psi{^+}_\text{mA}(\alpha\ket{1}_B + _B) + \beta\ket{0}$$
$$+ \frac1{2}\ket{\psi{^}-_\text{mA} (\alpha\ket{1}_B- \beta\ket{0}_B)$$
Глобальное состояние Алисы и кубитов Боба является суперпозицией четырех возможных состояний.
Совет
Хорошее упражнение заключается в том, чтобы убедиться, что глобальное состояние трех кубитов является одним из указанных выше. Это можно сделать, применив шлюз CNOT к кубитам сообщения и кубитом Алисы, а затем расширив состояние трех кубитов.
Алиса измеряет кубиты
Затем Алиса измеряет кубит сообщения и ее собственный кубит. Она не измеряет кубитов в $Z-основе$ как обычно, но она выбирает основу Колокола. Основа Bell состоит из четырех состояний Bell, \lbrace \ket{\phi^+}, \ket{\phi^-}, \ket{\psi^+}, ^-, \ket{\psi^-} \rbrace$. $
Измеряя кубитов сообщения и ее собственный кубит на основе Колокола, Алиса проектирует ее кубитов в одном из четырех состояний Колокола. Так как три кубита запутаны, результаты измерения коррелируются. Когда Алиса измеряет ее кубиты, кубит Боба также проецируется в коррелированного состояния.
Например, если Алиса измеряет ее кубиты и наблюдает состояние $\ket{\phi^-}$, то кубит Боба проецируется в состояние $\alpha\ket{0}_B - \beta\ket{1}_B$.
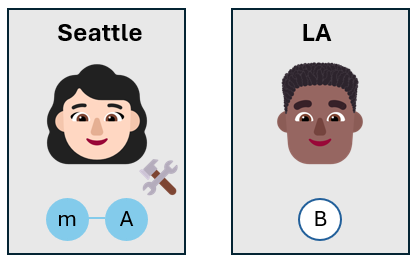
Алиса называет Боба
Алиса звонит Бобу и сообщает ему результаты ее измерений. Она использует классический канал связи, например телефонный звонок или текстовое сообщение.
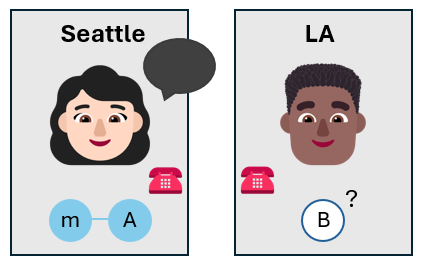
Боб теперь знает состояние своего собственного кубита, не имея необходимости измерять его. Состояние кубита Боба может не совпадать с состоянием кубита сообщения, что Алиса хотела телепортировать, но это близко к нему.
Боб применяет квантовую операцию
Затем Боб может восстановить исходное состояние кубита сообщения, применяя определенную квантовую операцию к его кубиту. Операция Боб выполняет зависит от того, что Алиса сказала ему по телефону.
Операция, выполняемая им, может быть воротами Паули $X$ , воротами Паули $Z$ , обоими или ни один.
Например, если результат измерения Алисы является ^-, Боб знает, что его кубит находится в состоянии $(\ket{0}\alpha_B -\ket{1}\beta _B)$.}$$\ket{\phi Он должен применить только ворота Паули Z, чтобы восстановить исходное состояние кубита сообщения.
| Меры Алисы | Боб применяется |
|---|---|
| $\ket{\phi^+}$ | Нет операции |
| $\ket{\phi^-}$ | Ворота Паули З |
| $\ket{\psi^+}$ | Ворота Паули X |
| $\ket{\psi^-}$ | Поли X ворота, за которым следуют ворота Паули З |
Эта окончательная операция эффективно телепортирует состояние кубита сообщения на кубит Боба. Миссия выполнена!
Внимание
Применение операции к кубитам не совпадает с измерением. Когда Боб применяет операцию, он не измеряет его кубит. Он применяет квантовую операцию, которая изменяет состояние кубита, но не сворачивает его.