Упражнение. Создание квантовой запутанности с помощью Q#
В предыдущем уроке вы узнали о концепции квантового запутания и состояния Колокола.
Теперь создадим квантовое запутание с помощью Q# и Azure Quantum Development Kit. Чтобы создать запутанность, необходимо применить две квантовые операции: операцию Hadamard и операцию Controlled-NOT (CNOT).
Сначала давайте посмотрим, как работают эти операции и как они создают запутанность.
Операция "Управляемое НЕ" (CNOT)
Если два кубита запутаны, состояние одного кубита зависит от состояния другого кубита. Поэтому для запутанного двух кубитов требуется операция, которая действует на обоих кубитах одновременно. Это называется многоквибитной операцией.
Чтобы создать квантовую запутанность, требуется многоквибитная CNOT операция, которая обозначает controled-NOT. Эта операция принимает два кубита в качестве входных данных, один выступает в качестве кубита управления, а другой — target кубитом. Операция CNOT перевернута состояние второго кубита ( target кубита), если, и только если состояние первого кубита (кубита управления) равно $|1\rangle$.
| Входные данные | Выходные данные |
|---|---|
| $\ket{00}$ | $\ket{00}$ |
| $\ket{01}$ | $\ket{01}$ |
| $\ket{10}$ | $\ket{11}$ |
| $\ket{11}$ | $\ket{10}$ |
В Q#операции CNOT выполняется операция на массиве двух кубитов, и она перевернута второй кубитов, если первый кубит имеет значение One.
Запутание с операциями Hadamard и CNOT
Применив hadamard, операцию и контролируемый не, Hоперацию, можно преобразовать два кубита в состоянии 00CNOT в состояние $|Bell ^+\rangle$1$\ket{\phi2}=\frac({\sqrt00}+|11\rangle).|\rangle$
Вот как это работает:
Возьмите два кубита в состоянии $|00\rangle$. Первый кубит является кубитом управления, а второй кубит — target кубитом.
Создайте состояние суперпозиции только в кубите элемента управления, применяя $H$.
$$H |0_c\rangle=\frac{1}{\sqrt{{2}}(|0_c\rangle+|1_c)\rangle$$
Совет
Подстроки ${}_c и $_t${}$ указать элемент управления и target кубиты.
$Примените оператор CNOT$ к кубите управления, который находится в состоянии суперпозиции, а target также кубит, который находится в $|состоянии 0_t\rangle$.
$$CNOT \frac{1}{\sqrt{2}}(\ket{0_c+}1_c)\ket{_t}\ket{0} CNOT =2\frac{1}{\sqrt(}0_c 0_t\ket{+}1_c 0_t|\ket{})2(CNOT 0_c 0_t + CNOT =$$1_c 0_t$$=\frac{){1}{\sqrt}\ket{}\ket{}=$$$$=2\frac{1}{\sqrt}(\ket{0_c 0_t+}1_c 1_t)\ket{}$$
Создайте квантовую запутанность в Q#
Начните с создания файла Q# в Visual Studio Code.
- Откройте Visual Studio Code.
- > Выберите новый текстовый файл и сохраните его в качестве Main.qs.
- Выберите представление —> палитра команд и типQ#target QIR Azure Quantum. Нажмите ВВОД.
- Выберите Q#: Неограниченно.
Создание состояния $\ket{\phiКолокола ^+}$
Начнем с создания состояния $\ket{\phiBell ^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$.
Сначала необходимо импортировать
Microsoft.Quantum.Diagnosticsпространство имен из стандартной библиотеки, содержащей функциюDumpMachine. Эта функция показывает текущее состояние кубитов. Скопируйте и вставьте следующий Q# код в файл Main.qs .import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;Совет
Вы также можете импортировать стандартную библиотеку, заменив
Microsoft.QuantumееStd. Например, выражениеimport Std.Diagnostics.*будет эквивалентноimport Microsoft.Quantum.Diagnostics.*.MainСоздайте операцию, возвращающую дваResultзначения типа, которые являются результатами измерения кубитов.import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { // Your code goes here }MainВнутри операции вы выделяете два кубита иq1q2, что будет запутано.import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); }Примените ворота Hadamard,
Hк первому кубитам,q1чтобы поместить его в состояние суперпозиции. Затем перепутает два кубита с помощьюCNOTоперации.import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); H(q1); CNOT(q1, q2); }Используйте функцию
DumpMachineдля отображения текущего состояния кубитов. Это не так же, как измерение кубитов.import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); H(q1); CNOT(q1, q2); DumpMachine(); }Измеряйте кубиты с помощью
Mоперации и сохраняйте результаты иm1m2. Затем используйтеResetоперацию для сброса кубитов. В Q#этом случае необходимо всегда сбрасывать кубиты в $|состояние 0\rangle$ .import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); H(q1); CNOT(q1, q2); DumpMachine(); let (m1, m2) = (M(q1), M(q2)); Reset(q1); Reset(q2); }Наконец, результаты измерения кубитов возвращаются с помощью инструкции
return. Файл Main.qs должен выглядеть следующим образом:import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); H(q1); CNOT(q1, q2); DumpMachine(); let (m1, m2) = (M(q1), M(q2)); Reset(q1); Reset(q2); return (m1, m2); }Чтобы запустить программу на встроенном симуляторе, нажмите кнопку "Выполнить над
Mainоперацией" или нажмите клавиши CTRL+F5. Выходные данные будут отображаться в консоли отладки.Результаты измерения коррелируются, поэтому в конце программы вы получаете результат
(Zero, Zero)или(One, One)с равной вероятностью.Вы можете визуализировать схему каналов, щелкнув канал из списка команд над операцией
Main. Схема схемы показывает ворота Hadamard, примененные к первому кубитам, и ворота CNOT, примененные к обоим кубитам.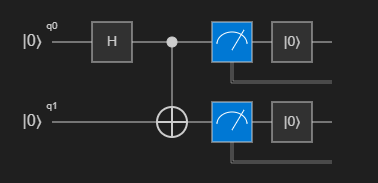
Как создать другие состояния Белла
Чтобы создать другие состояния Колокола, необходимо применить дополнительные операции Паули $X$ и $Z$ к кубитам.
Например, чтобы создать состояние $\ket{\phiBell ^-}=\frac1 2{\sqrt(}00-11|\rangle|\rangle),$ можно применить операцию Pauli $Z$ к кубите управления после применения шлюза Hadamard. Операция $Z$ перевернет состояние $\ket{+}$ на $\ket{-}$.
Совет
Состояния $\frac{{1}{\sqrt{2}}(|0\rangle+|1\rangle)$ и $\frac{1}{\sqrt{{2}}(|0\rangle –|1\rangle)$ также известны как $\ket{+}$ и $\ket{{-}$соответственно.
Вот как это работает:
Возьмите два кубита в состоянии $|00\rangle$.
Создайте состояние суперпозиции только в кубите элемента управления, применяя $H$.
$$H |0_c\rangle=\frac{{1}{\sqrt{2}}(|0_c\rangle+1_c)|\rangle +_c=\ket{}$$
$Примените операцию Z$ к кубите элемента управления.
$$Z \frac{{1}{\sqrt{{2}}(|0_c\rangle+|1_c\rangle)=\frac{1}{\sqrt{{2}}(|0_c-1_c\rangle|)_c\rangle=\ket{{-}$$
Примените $оператор CNOT$ к кубите управления и target кубите, который находится в состоянии $|0_t\rangle$.
$$ \frac{1}{\sqrt{2}}CNOT (\ket{0_c-1_c}\ket{)}_t \ket{0}=CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t-1_c 0_t}|\ket{})2(CNOT 0_c 0_t= - CNOT $$$$1_c 0_t=\frac{){1}{\sqrt}\ket{}\ket{}=$$$$=2\frac{1}{\sqrt}(\ket{0_c 0_t-1_c 1_t)}\ket{}$$
Аналогичным образом можно создать состояния $\ket{\psiBell ^+}$ и $\ket{\psi^-}$ путем применения операций Паули $X$ и $Z$ к кубитам.
- Состояние $\ket{\psiКолокола ^+}=\frac1 2{\sqrt(}01|\rangle+|10\rangle)$ можно создать, применив операцию Паули $X$ к target кубите после применения ворота Hadamard.
- Состояние $\ket{\psiКолокола ^-}=\frac1{\sqrt2}(|01-10\rangle|\rangle)$ можно создать, применив Поли $Z$ к кубите управления и Поли $X$ к target кубите после применения ворота Hadamard.
Создание состояния $\ket{\phiBell ^-}$ in Q#
Измените Q# код, чтобы создать состояние $\ket{\phiBell ^-}$. Файл Main.qs должен выглядеть следующим образом:
import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); H(q1); Z(q1); // Apply the Pauli Z operation to the control qubit CNOT(q1, q2); DumpMachine(); let (m1, m2) = (M(q1), M(q2)); Reset(q1); Reset(q2); return (m1, m2); }Чтобы запустить программу на встроенном симуляторе, нажмите кнопку "Выполнить над
Mainоперацией" или нажмите клавиши CTRL+F5. Выходные данные будут отображаться в консоли отладки.Вы можете визуализировать схему каналов, щелкнув канал из списка команд над операцией
Main. Схема схемы показывает ворота Hadamard, примененные к первому кубитам, ворота Паули $Z$ , примененные к первому кубитам, и ворота CNOT, примененные к обоим кубитам.
В следующем уроке вы узнаете, как использовать запутанность для отправки квантовой информации, процесса, известного как квантовое телепортирование.