Упражнение. Оценка ресурсов для реальной проблемы
В предыдущем уроке вы узнали основные понятия оценки ресурсов Azure Quantum и как его использовать.
В этом модуле вы оцените ресурсы, необходимые для разложения на множители 2048-разрядного целого числа с помощью алгоритма Шора. Алгоритм факторинга Shor является одним из самых известных квантовых алгоритмов. Он предлагает экспоненциальное ускорение по любому известному классическому алгоритму факторинга.
Классическая криптография использует физические или математические средства, такие как вычислительные трудности для выполнения задачи. Популярным протоколом шифрования является схема Rivest-Shamir-Adleman (RSA), основанная на предположении о сложности факторинга праймерных чисел с помощью классического компьютера.
Алгоритм Shor подразумевает, что достаточно крупные квантовые компьютеры могут нарушить криптографию открытого ключа. Оценка ресурсов, необходимых для алгоритма Шора, важна для оценки уязвимости этих типов криптографических схем.
В следующем упражнении вы вычислите оценки ресурсов для факторинга 2048-разрядного целого числа. Для этого приложения вы вычислите оценки физического ресурса непосредственно из предварительно вычисляемых логических оценок ресурсов. Для бюджета ошибок вы будете использовать $\epsilon = 1/3$.
Написание алгоритма Шора
В Visual Studio Code выберите палитру "Вид > команд" и выберите "Создать: создать записную книжку Jupyter".
Сохраните записную книжку как ShorRE.ipynb.
В первой ячейке импортируйте
qsharpпакет:import qsharpДобавьте новую ячейку и скопируйте и вставьте следующий код:
%%qsharp open Microsoft.Quantum.Arrays; open Microsoft.Quantum.Canon; open Microsoft.Quantum.Convert; open Microsoft.Quantum.Diagnostics; open Microsoft.Quantum.Intrinsic; open Microsoft.Quantum.Math; open Microsoft.Quantum.Measurement; open Microsoft.Quantum.Unstable.Arithmetic; open Microsoft.Quantum.ResourceEstimation; operation RunProgram() : Unit { let bitsize = 31; // When choosing parameters for `EstimateFrequency`, make sure that // generator and modules are not co-prime let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize); } // In this sample we concentrate on costing the `EstimateFrequency` // operation, which is the core quantum operation in Shors algorithm, and // we omit the classical pre- and post-processing. /// # Summary /// Estimates the frequency of a generator /// in the residue ring Z mod `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order (period) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## bitsize /// Number of bits needed to represent the modulus. /// /// # Output /// The numerator k of dyadic fraction k/2^bitsPrecision /// approximating s/r. operation EstimateFrequency( generator : Int, modulus : Int, bitsize : Int ) : Int { mutable frequencyEstimate = 0; let bitsPrecision = 2 * bitsize + 1; // Allocate qubits for the superposition of eigenstates of // the oracle that is used in period finding. use eigenstateRegister = Qubit[bitsize]; // Initialize eigenstateRegister to 1, which is a superposition of // the eigenstates we are estimating the phases of. // We first interpret the register as encoding an unsigned integer // in little endian encoding. ApplyXorInPlace(1, eigenstateRegister); let oracle = ApplyOrderFindingOracle(generator, modulus, _, _); // Use phase estimation with a semiclassical Fourier transform to // estimate the frequency. use c = Qubit(); for idx in bitsPrecision - 1..-1..0 { within { H(c); } apply { // `BeginEstimateCaching` and `EndEstimateCaching` are the operations // exposed by Azure Quantum Resource Estimator. These will instruct // resource counting such that the if-block will be executed // only once, its resources will be cached, and appended in // every other iteration. if BeginEstimateCaching("ControlledOracle", SingleVariant()) { Controlled oracle([c], (1 <<< idx, eigenstateRegister)); EndEstimateCaching(); } R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c); } if MResetZ(c) == One { set frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx); } } // Return all the qubits used for oracles eigenstate back to 0 state // using Microsoft.Quantum.Intrinsic.ResetAll. ResetAll(eigenstateRegister); return frequencyEstimate; } /// # Summary /// Interprets `target` as encoding unsigned little-endian integer k /// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where /// p is `power`, g is `generator` and N is `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order ( period ) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## power /// Power of `generator` by which `target` is multiplied. /// ## target /// Register interpreted as LittleEndian which is multiplied by /// given power of the generator. The multiplication is performed modulo /// `modulus`. internal operation ApplyOrderFindingOracle( generator : Int, modulus : Int, power : Int, target : Qubit[] ) : Unit is Adj + Ctl { // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We // also use `ExpModI` to compute a by which x must be multiplied. Also // note that we interpret target as unsigned integer in little-endian // encoding by using the `LittleEndian` type. ModularMultiplyByConstant(modulus, ExpModI(generator, power, modulus), target); } /// # Summary /// Performs modular in-place multiplication by a classical constant. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register (as LittleEndian) |𝑦⟩, this operation /// computes `(c*x) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular multiplication /// ## c /// Constant by which to multiply |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { use qs = Qubit[Length(y)]; for (idx, yq) in Enumerated(y) { let shiftedC = (c <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, shiftedC, qs)); } ApplyToEachCA(SWAP, Zipped(y, qs)); let invC = InverseModI(c, modulus); for (idx, yq) in Enumerated(y) { let shiftedC = (invC <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs)); } } /// # Summary /// Performs modular in-place addition of a classical constant into a /// quantum register. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register (as LittleEndian) |𝑦⟩, this operation /// computes `(x+c) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular addition /// ## c /// Constant to add to |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { body (...) { Controlled ModularAddConstant([], (modulus, c, y)); } controlled (ctrls, ...) { // We apply a custom strategy to control this operation instead of // letting the compiler create the controlled variant for us in which // the `Controlled` functor would be distributed over each operation // in the body. // // Here we can use some scratch memory to save ensure that at most one // control qubit is used for costly operations such as `AddConstant` // and `CompareGreaterThenOrEqualConstant`. if Length(ctrls) >= 2 { use control = Qubit(); within { Controlled X(ctrls, control); } apply { Controlled ModularAddConstant([control], (modulus, c, y)); } } else { use carry = Qubit(); Controlled AddConstant(ctrls, (c, y + [carry])); Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry])); Controlled AddConstant([carry], (modulus, y)); Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry)); } } } /// # Summary /// Performs in-place addition of a constant into a quantum register. /// /// # Description /// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive /// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩. /// /// # Input /// ## c /// Constant number to add to |𝑦⟩. /// ## y /// Quantum register of second summand and target; must not be empty. internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl { // We are using this version instead of the library version that is based // on Fourier angles to show an advantage of sparse simulation in this sample. let n = Length(y); Fact(n > 0, "Bit width must be at least 1"); Fact(c >= 0, "constant must not be negative"); Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}"); if c != 0 { // If c has j trailing zeroes than the j least significant bits // of y will not be affected by the addition and can therefore be // ignored by applying the addition only to the other qubits and // shifting c accordingly. let j = NTrailingZeroes(c); use x = Qubit[n - j]; within { ApplyXorInPlace(c >>> j, x); } apply { IncByLE(x, y[j...]); } } } /// # Summary /// Performs greater-than-or-equals comparison to a constant. /// /// # Description /// Toggles output qubit `target` if and only if input register `x` /// is greater than or equal to `c`. /// /// # Input /// ## c /// Constant value for comparison. /// ## x /// Quantum register to compare against. /// ## target /// Target qubit for comparison result. /// /// # Reference /// This construction is described in [Lemma 3, arXiv:2201.10200] internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit) : Unit is Adj+Ctl { let bitWidth = Length(x); if c == 0 { X(target); } elif c >= 2 ^ bitWidth { // do nothing } elif c == 2 ^ (bitWidth - 1) { ApplyLowTCNOT(Tail(x), target); } else { // normalize constant let l = NTrailingZeroes(c); let cNormalized = c >>> l; let xNormalized = x[l...]; let bitWidthNormalized = Length(xNormalized); let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized)); use qs = Qubit[bitWidthNormalized - 1]; let cs1 = [Head(xNormalized)] + Most(qs); let cs2 = Rest(xNormalized); within { for i in IndexRange(gates) { (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]); } } apply { ApplyLowTCNOT(Tail(qs), target); } } } /// # Summary /// Internal operation used in the implementation of GreaterThanOrEqualConstant. internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { within { ApplyToEachA(X, [control1, control2]); } apply { ApplyAnd(control1, control2, target); X(target); } } internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { body (...) { CCNOT(control1, control2, target); } adjoint (...) { H(target); if (M(target) == One) { X(target); CZ(control1, control2); } } } /// # Summary /// Returns the number of trailing zeroes of a number /// /// ## Example /// ```qsharp /// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0 /// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2 /// ``` internal function NTrailingZeroes(number : Int) : Int { mutable nZeroes = 0; mutable copy = number; while (copy % 2 == 0) { set nZeroes += 1; set copy /= 2; } return nZeroes; } /// # Summary /// An implementation for `CNOT` that when controlled using a single control uses /// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7. internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl { body (...) { CNOT(a, b); } adjoint self; controlled (ctls, ...) { // In this application this operation is used in a way that // it is controlled by at most one qubit. Fact(Length(ctls) <= 1, "At most one control line allowed"); if IsEmpty(ctls) { CNOT(a, b); } else { use q = Qubit(); within { ApplyAnd(Head(ctls), a, q); } apply { CNOT(q, b); } } } controlled adjoint self; }
Оценка алгоритма Шора
Теперь оцените физические ресурсы для RunProgram операции с помощью допущений по умолчанию. Добавьте новую ячейку и скопируйте и вставьте следующий код:
result = qsharp.estimate("RunProgram()")
result
Функция qsharp.estimate создает результирующий объект, который можно использовать для отображения таблицы с общим количеством физических ресурсов. Вы можете проверить сведения о затратах, совершите группы, которые содержат дополнительные сведения.
Например, свернуть группу параметров логического кубита, чтобы увидеть, что расстояние кода равно 21, а количество физических кубитов равно 882.
| Логический параметр кубита | Значение |
|---|---|
| Схема QEC | surface_code |
| Расстояние от кода | 21 |
| Физические кубиты | 882 |
| Время логического цикла | 8 милисек |
| Частота ошибок логического кубита | 3.00E-13 |
| Пересечение префактотора | 0,03 |
| Порог исправления ошибок | 0,01 |
| Формула логического цикла | (4 * + twoQubitGateTime 2 * ) * oneQubitMeasurementTimecodeDistance |
| Формула физических кубитов | 2 * codeDistance * codeDistance |
Совет
Для более компактной версии выходной таблицы можно использовать result.summary.
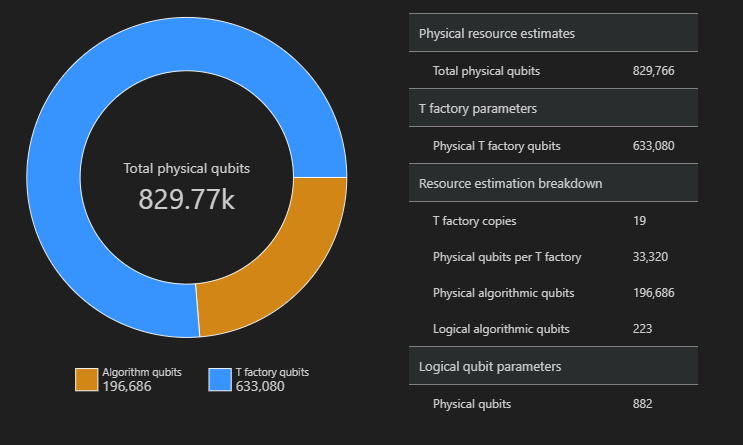
Визуализация схемы пространства
Распределение физических кубитов, используемых для алгоритма и фабрик T, является фактором, который может повлиять на структуру алгоритма. Пакет можно использовать qsharp-widgets для визуализации этого распределения, чтобы лучше понять предполагаемые требования к пространству алгоритма.
from qsharp_widgets import SpaceChart
SpaceChart(result)
В этом примере количество физических кубитов, необходимых для выполнения алгоритма, 829766, 196686 которых являются кубитами алгоритмов и 633080 из которых являются кубитами фабрики.
Сравнение оценок ресурсов для различных технологий кубитов
Средство оценки ресурсов Azure Quantum позволяет выполнять несколько конфигураций целевых параметров и сравнивать результаты. Это полезно, если вы хотите сравнить стоимость различных моделей кубитов, схем QEC или бюджетов ошибок.
Вы также можете создать список параметров оценки с помощью EstimatorParams объекта.
from qsharp.estimator import EstimatorParams, QubitParams, QECScheme, LogicalCounts
labels = ["Gate-based µs, 10⁻³", "Gate-based µs, 10⁻⁴", "Gate-based ns, 10⁻³", "Gate-based ns, 10⁻⁴", "Majorana ns, 10⁻⁴", "Majorana ns, 10⁻⁶"]
params = EstimatorParams(6)
params.error_budget = 0.333
params.items[0].qubit_params.name = QubitParams.GATE_US_E3
params.items[1].qubit_params.name = QubitParams.GATE_US_E4
params.items[2].qubit_params.name = QubitParams.GATE_NS_E3
params.items[3].qubit_params.name = QubitParams.GATE_NS_E4
params.items[4].qubit_params.name = QubitParams.MAJ_NS_E4
params.items[4].qec_scheme.name = QECScheme.FLOQUET_CODE
params.items[5].qubit_params.name = QubitParams.MAJ_NS_E6
params.items[5].qec_scheme.name = QECScheme.FLOQUET_CODE
qsharp.estimate("RunProgram()", params=params).summary_data_frame(labels=labels)
| Модель Кубита | Логические кубиты | Логическая глубина | Состояния T | Расстояние от кода | Фабрики T | Доля фабрики T | Физические кубиты | rQOPS | Физическая среда выполнения |
|---|---|---|---|---|---|---|---|---|---|
| Шлюз на основе μs, 10⁻️ | 223 3.64M | 4.70M | 17 | 13 | 40.54 % | 216.77k | 21.86k | 10 часов | |
| Шлюз на основе μs, 10⁻⁴ | 223 | 3.64M | 4.70M | 9 | 14 | 43.17 % | 63.57k | 41.30k | 5 часов |
| Шлюз на основе ns, 10⁻️ | 223 3.64M | 4.70M | 17 | 16 | 69.08 % | 416.89k | 32.79M | 25 с | |
| Шлюз на основе ns, 10⁻⁴ | 223 3.64M | 4.70M | 9 | 14 | 43.17 % | 63.57k | 61.94M | 13 с | |
| Майорана ns, 10⁻⁴ | 223 3.64M | 4.70M | 9 | 19 | 82.75 % | 501.48k | 82.59M | 10 с | |
| Майорана ns, 10⁻⁶ | 223 3.64M | 4.70M | 5 | 13 | 31.47 % | 42.96k | 148.67M | 5 с |
Извлечение оценок ресурсов из счетчиков логических ресурсов
Если вы уже знаете некоторые оценки для операции, ресурс оценки позволяет включить известные оценки в общую стоимость программы, чтобы сократить время выполнения. Класс можно использовать LogicalCounts для извлечения оценки логических ресурсов из предварительно вычисляемых значений оценки ресурсов.
Выберите код , чтобы добавить новую ячейку, а затем введите и запустите следующий код:
logical_counts = LogicalCounts({
'numQubits': 12581,
'tCount': 12,
'rotationCount': 12,
'rotationDepth': 12,
'cczCount': 3731607428,
'measurementCount': 1078154040})
logical_counts.estimate(params).summary_data_frame(labels=labels)
| Модель Кубита | Логические кубиты | Логическая глубина | Состояния T | Расстояние от кода | Фабрики T | Доля фабрики T | Физические кубиты | Физическая среда выполнения |
|---|---|---|---|---|---|---|---|---|
| Шлюз на основе μs, 10⁻️ | 25481 | 1.2e+10 | 1.5e+10 | 27 | 13 | 0,6 % | 37.38M | 6 лет |
| Шлюз на основе μs, 10⁻⁴ | 25481 | 1.2e+10 | 1.5e+10 | 13 | 14 | 0,8 % | 8.68M | 3 года |
| Шлюз на основе ns, 10⁻️ | 25481 | 1.2e+10 | 1.5e+10 | 27 | 15 | 1,3 % | 37,65 млн | 2 дня |
| Шлюз на основе ns, 10⁻⁴ | 25481 | 1.2e+10 | 1.5e+10 | 13 | 18 | 1,2 % | 8.72M | 18 часов |
| Майорана ns, 10⁻⁴ | 25481 | 1.2e+10 | 1.5e+10 | 15 | 15 | 1,3 % | 26.11M | 15 часов |
| Майорана ns, 10⁻⁶ | 25481 | 1.2e+10 | 1.5e+10 | 7 | 13 | 0,5 % | 6.25M | 7 часов |
Заключение
В худшем сценарии квантовый компьютер с использованием воротных кубитов (кубитов, имеющих время работы в режиме наносеконд, таких как сверхпроводящие кубиты), и код QEC поверхности потребует шесть лет и 37,38 миллиона кубитов, чтобы фактор 2048-разрядного целого числа с помощью алгоритма Шора.
Если вы используете другую технологию кубитов ( например, шлюзы ns ion кубитов) и один и тот же код поверхности, количество кубитов не меняется много, но среда выполнения становится два дня в худшем случае и 18 часов в оптимистическом случае. Если вы изменяете технологию кубита и код QEC ( например, с помощью кубитов на основе Майораны) фактор 2048-разрядного целого числа с помощью алгоритма Shor можно сделать в часах с массивом 6,25 миллиона кубитов в лучшем сценарии.
Из эксперимента можно заключить, что использование кубитов Majorana и кода Floquet QEC является лучшим выбором для выполнения алгоритма Shor и коэффициента 2048-разрядного целого числа.