Преобразования матрицы в SkiaSharp
Подробнее о преобразованиях SkiaSharp с помощью универсальной матрицы преобразования
Все преобразования, применяемые к SKCanvas объекту, объединяются в одном экземпляре SKMatrix структуры. Это стандартная матрица преобразования 3–3, аналогичная матрице всех современных графических систем 2D.
Как вы видели, вы можете использовать преобразования в SkiaSharp, не зная о матрице преобразования, но матрица преобразования важна с теоретических перспектив, и это важно при использовании преобразований для изменения путей или обработки сложных сенсорных входных данных, оба из которых показаны в этой статье и далее.

Текущая матрица преобразования, применяемая к ней SKCanvas , доступна в любое время путем доступа к свойству только для TotalMatrix чтения. Вы можете задать новую матрицу преобразования с помощью SetMatrix метода, и можно восстановить матрицу преобразования до значений по умолчанию, вызвав вызов ResetMatrix.
Единственным другим SKCanvas элементом, который напрямую работает с преобразованием матрицы холста, является Concat объединение двух матриц путем умножения их вместе.
Матрица преобразования по умолчанию является матрицей идентификации и состоит из 1 в диагональных ячейках и 0 везде:
| 1 0 0 | | 0 1 0 | | 0 0 1 |
Матрицу удостоверений можно создать с помощью статического SKMatrix.MakeIdentity метода:
SKMatrix matrix = SKMatrix.MakeIdentity();
Конструктор SKMatrixпо умолчанию не возвращает матрицу удостоверений. Он возвращает матрицу со всеми ячейками, равными нулю. Не используйте SKMatrix конструктор, если вы не планируете задать эти ячейки вручную.
Когда SkiaSharp отрисовывает графический объект, каждая точка (x, y) фактически преобразуется в матрицу 1–3 с 1 в третьем столбце:
| x y 1 |
Эта матрица от 1 до 3 представляет трехмерную точку с координатами Z, равным 1. Существуют математические причины (рассмотренные далее), почему двухмерное преобразование матрицы требует работы в трех измерениях. Вы можете думать об этой матрице от 1 до 3 как о точке в трехмерной системе координат, но всегда на 2D-плоскости, где Z равно 1.
Затем эта матрица 1 на 3 умножается на матрицу преобразования, а результатом является точка, отрисоваемая на холсте:
| 1 0 0 |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| 0 0 1 |
Используя стандартное умножение матрицы, преобразованные точки приведены следующим образом:
x' = x
y' = y
z' = 1
Это преобразование по умолчанию.
Translate При вызове метода в SKCanvas объекте tx аргументы ty метода становятся первыми двумя ячейками Translate в третьей строке матрицы преобразования:
| 1 0 0 | | 0 1 0 | | tx ty 1 |
Умножение теперь выглядит следующим образом:
| 1 0 0 |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| tx ty 1 |
Ниже приведены формулы преобразования:
x' = x + tx
y' = y + ty
Коэффициенты масштабирования имеют значение по умолчанию 1. При вызове Scale метода в новом SKCanvas объекте результирующая матрица преобразования содержит sx и sy аргументы в диагональных ячейках:
| sx 0 0 |
| x y 1 | × | 0 sy 0 | = | x' y' z' |
| 0 0 1 |
Формулы преобразования приведены следующим образом:
x' = sx · x
y' = sy · y
Матрица преобразования после вызова Skew содержит два аргумента в ячейках матрицы, смежных с коэффициентами масштабирования:
│ 1 ySkew 0 │
| x y 1 | × │ xSkew 1 0 │ = | x' y' z' |
│ 0 0 1 │
Формулы преобразования:
x' = x + xSkew · y
y' = ySkew · x + y
Для вызова RotateDegrees или RotateRadians для угла α матрица преобразования выглядит следующим образом:
│ cos(α) sin(α) 0 │
| x y 1 | × │ –sin(α) cos(α) 0 │ = | x' y' z' |
│ 0 0 1 │
Ниже приведены формулы преобразования:
x' = cos(α) · x - sin(α) · y
y' = sin(α) · x - cos(α) · y
Если α равен 0 градусам, это матрица идентификации. Если α составляет 180 градусов, матрица преобразования выглядит следующим образом:
| –1 0 0 | | 0 –1 0 | | 0 0 1 |
Поворот в 180 градусов эквивалентен перевернутию объекта по горизонтали и вертикали, что также достигается путем установки коэффициентов масштабирования –1.
Все эти типы преобразований классифицируются как аффинные преобразования. Аффинные преобразования никогда не включают третий столбец матрицы, который остается в значениях по умолчанию 0, 0 и 1. В статье преобразования, отличные от аффинных преобразований, рассматриваются неаффинные преобразования.
умножение матриц
Одним из значительных преимуществ с использованием матрицы преобразования является то, что составные преобразования можно получить путем умножения матрицы, который часто называется в документации SkiaSharp как объединение. Многие методы преобразования, связанные с преобразованием, SKCanvas ссылаются на "предварительное объединение" или "предварительная сцепление". Это относится к порядку умножения, что важно, поскольку умножение матрицы не является коммутативным.
Например, в документации по Translate методу говорится, что она "Предварительно сцепить текущую матрицу с указанным переводом", в то время как в документации Scale по методу говорится, что она "Предварительно сцепить текущую матрицу с указанным масштабом".
Это означает, что преобразование, указанное вызовом метода, является умножением (левый операнд), а текущая матрица преобразования — умножение (правый операнд).
Предположим, что Translate за ним следует Scale:
canvas.Translate(tx, ty);
canvas.Scale(sx, sy);
Преобразование Scale умножается на Translate преобразование для матрицы составного преобразования:
| sx 0 0 | | 1 0 0 | | sx 0 0 | | 0 sy 0 | × | 0 1 0 | = | 0 sy 0 | | 0 0 1 | | tx ty 1 | | tx ty 1 |
Scale можно вызвать до Translate следующего:
canvas.Scale(sx, sy);
canvas.Translate(tx, ty);
В этом случае порядок умножения обратная, а коэффициенты масштабирования эффективно применяются к факторам перевода:
| 1 0 0 | | sx 0 0 | | sx 0 0 | | 0 1 0 | × | 0 sy 0 | = | 0 sy 0 | | tx ty 1 | | 0 0 1 | | tx·sx ty·sy 1 |
Ниже приведен Scale метод с точкой сводных данных:
canvas.Scale(sx, sy, px, py);
Это эквивалентно следующим вызовам перевода и масштабирования:
canvas.Translate(px, py);
canvas.Scale(sx, sy);
canvas.Translate(–px, –py);
Три матрицы преобразования умножаются в обратном порядке от способа отображения методов в коде:
| 1 0 0 | | sx 0 0 | | 1 0 0 | | sx 0 0 | | 0 1 0 | × | 0 sy 0 | × | 0 1 0 | = | 0 sy 0 | | –px –py 1 | | 0 0 1 | | px py 1 | | px–px·sx py–py·sy 1 |
Структура SKMatrix
Структура SKMatrix определяет девять свойств типа float чтения и записи, соответствующих девяти ячейкам матрицы преобразования:
│ ScaleX SkewY Persp0 │ │ SkewX ScaleY Persp1 │ │ TransX TransY Persp2 │
SKMatrix также определяет свойство с именем Values типа float[]. Это свойство можно использовать для задания или получения девяти значений в одном снимке в порядке ScaleX, SkewX, TransXTransYScaleYPersp0SkewYPersp1и .Persp2
Ячейки и ячейки рассматриваются в статье "Неаффинные преобразования".Persp2Persp0Persp1 Если эти ячейки имеют значения по умолчанию 0, 0 и 1, преобразование умножается на точку координат, как показано ниже:
│ ScaleX SkewY 0 │
| x y 1 | × │ SkewX ScaleY 0 │ = | x' y' z' |
│ TransX TransY 1 │
x' = ScaleX · x + SkewX · y + TransX
y' = SkewX · x + ScaleY · y + TransY
z' = 1
Это полное двухмерное аффинное преобразование. Преобразование аффин сохраняет параллельные линии, что означает, что прямоугольник никогда не преобразуется в что-либо, кроме параллелограммы.
Структура SKMatrix определяет несколько статических методов для создания SKMatrix значений. Эти все возвращаемые SKMatrix значения:
MakeTranslationMakeScaleMakeScaleс точкой сводных точекMakeRotationдля угла в радианахMakeRotationдля угла в радианах с точкой сводных точекMakeRotationDegreesMakeRotationDegreesс точкой сводных точекMakeSkew
SKMatrix также определяет несколько статических методов, сцепляющих две матрицы, что означает умножение их. Эти методы называются Concat, PostConcatи PreConcatесть две версии каждого. Эти методы не имеют возвращаемых значений; вместо этого они ссылаются на существующие SKMatrix значения с помощью ref аргументов. В следующем примере , ABи R (для результата) являются всеми SKMatrix значениями.
Эти два Concat метода называются следующим образом:
SKMatrix.Concat(ref R, A, B);
SKMatrix.Concat(ref R, ref A, ref B);
Они выполняют следующее умножение:
R = B × A
Другие методы имеют только два параметра. Первый параметр изменяется и возвращается из вызова метода, содержит произведение двух матриц. Эти два PostConcat метода называются следующим образом:
SKMatrix.PostConcat(ref A, B);
SKMatrix.PostConcat(ref A, ref B);
Эти вызовы выполняют следующую операцию:
A = A × B
Два PreConcat метода похожи:
SKMatrix.PreConcat(ref A, B);
SKMatrix.PreConcat(ref A, ref B);
Эти вызовы выполняют следующую операцию:
A = B × A
Версии этих методов со всеми ref аргументами немного эффективнее при вызове базовых реализаций, но это может быть запутано для кого-то, кто читает код и предполагает, что все, что с ref аргументом изменяется методом. Кроме того, часто удобно передавать аргумент, который является результатом одного из Make методов, например:
SKMatrix result;
SKMatrix.Concat(result, SKMatrix.MakeTranslation(100, 100),
SKMatrix.MakeScale(3, 3));
При этом создается следующая матрица:
│ 3 0 0 │ │ 0 3 0 │ │ 100 100 1 │
Это преобразование масштабирования, умноженное на преобразование перевода. В этом случае SKMatrix структура предоставляет ярлык с методом с именем SetScaleTranslate:
SKMatrix R = new SKMatrix();
R.SetScaleTranslate(3, 3, 100, 100);
Это один из нескольких раз, когда он безопасно использовать SKMatrix конструктор. Метод SetScaleTranslate задает все девять ячеек матрицы. Также можно использовать SKMatrix конструктор со статическими Rotate и RotateDegrees методами:
SKMatrix R = new SKMatrix();
SKMatrix.Rotate(ref R, radians);
SKMatrix.Rotate(ref R, radians, px, py);
SKMatrix.RotateDegrees(ref R, degrees);
SKMatrix.RotateDegrees(ref R, degrees, px, py);
Эти методы не объединяют преобразование поворота к существующему преобразованию. Методы задают все ячейки матрицы. Они функционально идентичны MakeRotation и MakeRotationDegrees методы, за исключением того, что они не создают экземпляр SKMatrix значения.
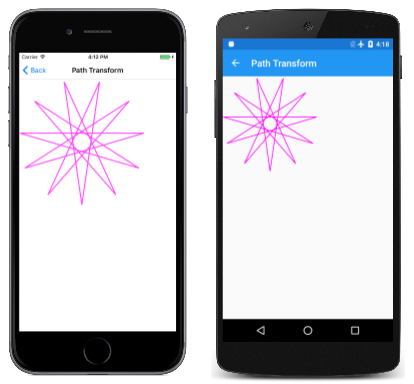
Предположим, что у вас есть SKPath объект, который вы хотите отобразить, но вы предпочитаете, что он имеет несколько другую ориентацию или другую центральную точку. Вы можете изменить все координаты этого пути, вызвав Transform метод SKPath с аргументом SKMatrix . На странице преобразования пути показано, как это сделать. Класс PathTransform ссылается на HendecagramPath объект в поле, но использует его конструктор для применения преобразования к такому пути:
public class PathTransformPage : ContentPage
{
SKPath transformedPath = HendecagramArrayPage.HendecagramPath;
public PathTransformPage()
{
Title = "Path Transform";
SKCanvasView canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
SKMatrix matrix = SKMatrix.MakeScale(3, 3);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeRotationDegrees(360f / 22));
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(300, 300));
transformedPath.Transform(matrix);
}
...
}
Объект HendecagramPath имеет центр (0, 0), а 11 точек звезды простираются из этого центра на 100 единиц во всех направлениях. Это означает, что путь имеет как положительные, так и отрицательные координаты. Страница преобразования пути предпочитает работать со звездой в три раза больше и со всеми положительными координатами. Кроме того, он не хочет, чтобы одна точка звезды указывала прямо вверх. Он хочет вместо того, чтобы одна точка звезды указывала прямо вниз. (Так как звезда имеет 11 очков, она не может иметь обоих.) Для этого требуется поворот звезды на 360 градусов, разделенных на 22.
Конструктор создает SKMatrix объект из трех отдельных преобразований с помощью PostConcat метода со следующим шаблоном, где A, B и C являются экземплярами SKMatrix:
SKMatrix matrix = A;
SKMatrix.PostConcat(ref A, B);
SKMatrix.PostConcat(ref A, C);
Это ряд последовательных умножений, поэтому результат выглядит следующим образом:
A × B × C
Последовательные умножения помогают понять, что делает каждое преобразование. Преобразование масштабирования увеличивает размер координат пути на 3, поэтому координаты варьируются от –300 до 300. Преобразование поворота поворачивает звезду вокруг его источника. Преобразование преобразования затем сдвигает его на 300 пикселей вправо и вниз, поэтому все координаты становятся положительными.
Существуют и другие последовательности, которые создают ту же матрицу. Вот еще один:
SKMatrix matrix = SKMatrix.MakeRotationDegrees(360f / 22);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(100, 100));
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(3, 3));
Это поворачивает путь вокруг центра сначала, а затем преобразует его 100 пикселей вправо и вниз, чтобы все координаты были положительными. Затем звезда увеличивается в размере относительно нового левого верхнего угла, который является точкой (0, 0).
Обработчик PaintSurface может просто отобразить этот путь:
public class PathTransformPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Magenta;
paint.StrokeWidth = 5;
canvas.DrawPath(transformedPath, paint);
}
}
}
Он отображается в левом верхнем углу холста:
Конструктор этой программы применяет матрицу к пути со следующим вызовом:
transformedPath.Transform(matrix);
Путь не сохраняет эту матрицу в качестве свойства. Вместо этого он применяет преобразование ко всем координатам пути. При Transform повторном вызове преобразование применяется снова, и единственным способом возврата является применение другой матрицы, которая отменяет преобразование. К счастью, SKMatrix структура определяет TryInvert метод, который получает матрицу, которая изменяет данную матрицу:
SKMatrix inverse;
bool success = matrix.TryInverse(out inverse);
Метод вызывается TryInverse , так как не все матрицы являются инвертируемыми, но невертываемая матрица, скорее всего, не будет использоваться для преобразования графики.
Вы также можете применить преобразование матрицы к SKPoint значению, массиву точек, SKRectа также даже одному числу в программе. Структура SKMatrix поддерживает эти операции с коллекцией методов, начинающихся с слова Map, например:
SKPoint transformedPoint = matrix.MapPoint(point);
SKPoint transformedPoint = matrix.MapPoint(x, y);
SKPoint[] transformedPoints = matrix.MapPoints(pointArray);
float transformedValue = matrix.MapRadius(floatValue);
SKRect transformedRect = matrix.MapRect(rect);
Если вы используете этот последний метод, помните, что SKRect структура не может представлять повернутый прямоугольник. Метод имеет смысл только для SKMatrix значения, представляющего преобразование и масштабирование.
Интерактивное экспериментирование
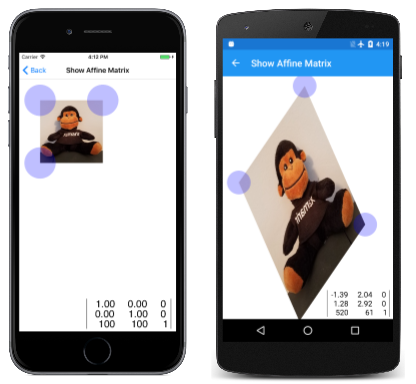
Один из способов получить представление о преобразовании аффина заключается в интерактивном перемещении трех углов растрового изображения на экране и просмотре результатов преобразования. Это идея страницы "Показать аффин матрицу ". Для этой страницы требуются два других класса, которые также используются в других демонстрациях:
Класс TouchPoint отображает полупрозрачный круг, который можно перетащить на экран. TouchPoint требует, чтобы SKCanvasView элемент, который является родительским элементом SKCanvasView присоединенного TouchEffect объекта. Установите свойство Capture в значение true. В обработчике TouchAction событий программа должна вызывать ProcessTouchEvent метод для TouchPoint каждого TouchPoint экземпляра. Метод возвращается true , если событие касания привело к перемещению точек касания. Кроме того, PaintSurface обработчик должен вызвать Paint метод в каждом TouchPoint экземпляре, передав его объекту SKCanvas .
TouchPoint демонстрирует общий способ инкапсулировать визуальный элемент SkiaSharp в отдельном классе. Класс может определять свойства для указания характеристик визуального элемента, а метод с именем Paint с аргументом SKCanvas может отобразить его.
Свойство CenterTouchPoint указывает расположение объекта. Это свойство можно задать для инициализации расположения; Свойство изменяется, когда пользователь перетаскивает круг по холсту.
Для параметра Show Affine Matrix Page также требуется MatrixDisplay класс. Этот класс отображает ячейки SKMatrix объекта. Он имеет два открытых метода: Measure для получения измерений отрисованной матрицы и Paint отображения. Класс содержит MatrixPaint свойство типа SKPaint , которое можно заменить на другой размер шрифта или цвет.
Файл ShowAffineMatrixPage.xaml создает SKCanvasView экземпляр и присоединяет объект TouchEffect. Файл ShowAffineMatrixPage.xaml.cs кодовой части создает три TouchPoint объекта, а затем задает для них позиции, соответствующие трем углам растрового изображения, который загружается из внедренного ресурса:
public partial class ShowAffineMatrixPage : ContentPage
{
SKMatrix matrix;
SKBitmap bitmap;
SKSize bitmapSize;
TouchPoint[] touchPoints = new TouchPoint[3];
MatrixDisplay matrixDisplay = new MatrixDisplay();
public ShowAffineMatrixPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
touchPoints[0] = new TouchPoint(100, 100); // upper-left corner
touchPoints[1] = new TouchPoint(bitmap.Width + 100, 100); // upper-right corner
touchPoints[2] = new TouchPoint(100, bitmap.Height + 100); // lower-left corner
bitmapSize = new SKSize(bitmap.Width, bitmap.Height);
matrix = ComputeMatrix(bitmapSize, touchPoints[0].Center,
touchPoints[1].Center,
touchPoints[2].Center);
}
...
}
Аффинная матрица однозначно определяется тремя точками. Три TouchPoint объекта соответствуют верхнему левому, правому верхнему и нижнему левому углам растрового изображения. Так как аффинная матрица может преобразовывать прямоугольник в параллелограмму, четвертая точка подразумевается другими тремя. Конструктор завершает вызовом ComputeMatrix, который вычисляет ячейки SKMatrix объекта из этих трех точек.
Обработчик TouchAction вызывает ProcessTouchEvent метод каждого TouchPoint. Значение scale преобразуется из Xamarin.Forms координат в пиксели:
public partial class ShowAffineMatrixPage : ContentPage
{
...
void OnTouchEffectAction(object sender, TouchActionEventArgs args)
{
bool touchPointMoved = false;
foreach (TouchPoint touchPoint in touchPoints)
{
float scale = canvasView.CanvasSize.Width / (float)canvasView.Width;
SKPoint point = new SKPoint(scale * (float)args.Location.X,
scale * (float)args.Location.Y);
touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, point);
}
if (touchPointMoved)
{
matrix = ComputeMatrix(bitmapSize, touchPoints[0].Center,
touchPoints[1].Center,
touchPoints[2].Center);
canvasView.InvalidateSurface();
}
}
...
}
TouchPoint При перемещении метода метод снова вызывается ComputeMatrix и делает поверхность недопустимой.
Метод ComputeMatrix определяет матрицу, подразумеваемую этими тремя точками. Матрица, называемая A преобразованием прямоугольника с одним пикселем в параллелограмму на основе трех точек, а преобразование масштабирования, называемое S масштабированием, масштабирует растровое изображение до прямоугольника с одним пикселем. Составная матрица ×SA:
public partial class ShowAffineMatrixPage : ContentPage
{
...
static SKMatrix ComputeMatrix(SKSize size, SKPoint ptUL, SKPoint ptUR, SKPoint ptLL)
{
// Scale transform
SKMatrix S = SKMatrix.MakeScale(1 / size.Width, 1 / size.Height);
// Affine transform
SKMatrix A = new SKMatrix
{
ScaleX = ptUR.X - ptUL.X,
SkewY = ptUR.Y - ptUL.Y,
SkewX = ptLL.X - ptUL.X,
ScaleY = ptLL.Y - ptUL.Y,
TransX = ptUL.X,
TransY = ptUL.Y,
Persp2 = 1
};
SKMatrix result = SKMatrix.MakeIdentity();
SKMatrix.Concat(ref result, A, S);
return result;
}
...
}
Наконец, PaintSurface метод отрисовывает растровое изображение на основе этой матрицы, отображает матрицу в нижней части экрана и отрисовывает точки касания в трех углах растрового изображения:
public partial class ShowAffineMatrixPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Display the bitmap using the matrix
canvas.Save();
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, 0, 0);
canvas.Restore();
// Display the matrix in the lower-right corner
SKSize matrixSize = matrixDisplay.Measure(matrix);
matrixDisplay.Paint(canvas, matrix,
new SKPoint(info.Width - matrixSize.Width,
info.Height - matrixSize.Height));
// Display the touchpoints
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
}
На экране iOS ниже показана растровая карта при первой загрузке страницы, а два других экрана отображают его после некоторых манипуляций:
Хотя кажется, что сенсорные точки перетаскивают угла растрового изображения, это только иллюзия. Матрица, вычисляемая из точек касания, преобразует растровое изображение, чтобы угловы совпадали с точками касания.
Это более естественно для пользователей для перемещения, изменения размера и поворота растровых изображений не путем перетаскивания углов, а с помощью одного или двух пальцев непосредственно на объекте для перетаскивания, сжатия и поворота. Это описано в следующей статье касания манипуляции.
Причина матрицы 3–3
Возможно, предполагается, что двухмерная графическая система потребует только матрицы преобразования 2-к-2:
│ ScaleX SkewY │
| x y | × │ │ = | x' y' |
│ SkewX ScaleY │
Это работает для масштабирования, поворота и даже размыкания, но он не может быть самым основным преобразованием, который является переводом.
Проблема заключается в том, что матрица 2-к-2 представляет линейное преобразование в двух измерениях. Линейное преобразование сохраняет некоторые основные арифметические операции, но одно из последствий заключается в том, что линейное преобразование никогда не изменяет точку (0, 0). Линейное преобразование делает перевод невозможным.
В трех измерениях матрица линейного преобразования выглядит следующим образом:
│ ScaleX SkewYX SkewZX │
| x y z | × │ SkewXY ScaleY SkewZY │ = | x' y' z' |
│ SkewXZ SkewYZ ScaleZ │
Ячейка, помеченная SkewXY , означает, что значение искажает координату X на основе значений Y; ячейка SkewXZ означает, что значение перемежает координату X на основе значений Z; и значения скошены аналогично другим Skew ячейкам.
Эту трехмерную матрицу преобразования можно ограничить двумерной плоскости путем установки SkewZX и SkewZY 0 и ScaleZ до 1:
│ ScaleX SkewYX 0 │
| x y z | × │ SkewXY ScaleY 0 │ = | x' y' z' |
│ SkewXZ SkewYZ 1 │
Если двухмерная графика полностью рисуется на плоскости в трехмерном пространстве, где Z равно 1, умножение преобразования выглядит следующим образом:
│ ScaleX SkewYX 0 │
| x y 1 | × │ SkewXY ScaleY 0 │ = | x' y' 1 |
│ SkewXZ SkewYZ 1 │
Все остается на двухмерной плоскости, где Z равно 1, но SkewXZ и SkewYZ ячейки фактически становятся двумерными факторами перевода.
Вот как трехмерное линейное преобразование служит двумерным нелинейным преобразованием. (По аналогии преобразования в трехмерной графике основаны на матрице 4-к-4.)
Структура SKMatrix в SkiaSharp определяет свойства для этой третьей строки:
│ ScaleX SkewY Persp0 │
| x y 1 | × │ SkewX ScaleY Persp1 │ = | x' y' z` |
│ TransX TransY Persp2 │
Ненулевых значений Persp0 и Persp1 приводит к преобразованиям, которые перемещают объекты из двухмерной плоскости, где Z равен 1. Что происходит, когда эти объекты перемещаются обратно в этот плоскость, рассматриваются в статье о неаффинных преобразованиях.