Трехмерные повороты в SkiaSharp
Используйте неаффинные преобразования для поворота трехмерных объектов в трехмерном пространстве.
Одним из распространенных применений неаффинных преобразований является имитация поворота 2D-объекта в трехмерном пространстве:
Это задание предполагает работу с трехмерными поворотами, а затем производным от аффинного SKMatrix преобразования, выполняющего эти трехмерные повороты.
Трудно разработать это SKMatrix преобразование исключительно в двух измерениях. Задание становится гораздо проще, когда эта матрица 3-к-3 является производным от матрицы 4-к-4, используемой в трехмерной графике. SkiaSharp включает SKMatrix44 класс для этой цели, но некоторый фон в трехмерной графике необходим для понимания трехмерных поворотов и матрицы преобразования 4-к-4.
Трехмерная система координат добавляет третью ось под названием Z. Концептуально ось Z находится в правых углах экрана. Точки координат в трехмерном пространстве указываются с тремя числами: (x, y, z). В 3D-системе координат, используемой в этой статье, увеличение значений X справа и увеличение значений Y опускаются так же, как в двух измерениях. Увеличение положительных значений Z выходит из экрана. Источник — левый верхний угол, как и в 2D-графике. Экран можно рассматривать как плоскость XY с осью Z в правых углах этой плоскости.
Это называется левой системой координат. Если вы указываете указатель на указатель на левую руку в направлении положительных координат X (справа), а средний палец в направлении увеличения координат Y (вниз), то ваш пальцем в направлении увеличения координат Z — вытягивается с экрана.
В трехмерной графике преобразования основаны на матрице 4–4. Ниже приведена матрица удостоверений 4-4:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 0 | | 0 0 0 1 |
При работе с матрицей 4–4 удобно идентифицировать ячейки со своими номерами строк и столбцов:
| M11 M12 M13 M14 | | M21 M22 M23 M24 | | M31 M32 M33 M34 | | M41 M42 M43 M44 |
Однако класс SkiaSharp Matrix44 немного отличается. Единственным способом установки или получения отдельных значений SKMatrix44 ячеек является использование Item индексатора. Индексы строк и столбцов основаны на нулях, а не на основе одного, а строки и столбцы переключаются. Доступ к ячейке M14 на приведенной выше схеме осуществляется с помощью индексатора [3, 0] в объекте SKMatrix44 .
В трехмерной графической системе трехмерная точка (x, y, z) преобразуется в матрицу 1 на 4 для умножения на матрицу преобразования 4-на-4:
| M11 M12 M13 M14 |
| x y z 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Аналогичные 2D-преобразованиям, которые происходят в трех измерениях, предполагается, что трехмерные преобразования выполняются в четырех измерениях. Четвертое измерение называется W, и предполагается, что трехмерное пространство существует в пределах 4D-пространства, где координаты W равны 1. Формулы преобразования приведены следующим образом:
x' = M11·x + M21·y + M31·z + M41
y' = M12·x + M22·y + M32·z + M42
z' = M13·x + M23·y + M33·z + M43
w' = M14·x + M24·y + M34·z + M44
Очевидно, что из формул преобразования ячейки M11, M22M33 являются факторами масштабирования в направлениях X, Y и Z, а M41M42M43 также являются факторами перевода в направлениях X, Y и Z.
Чтобы преобразовать эти координаты обратно в трехмерное пространство, где W равно 1, координаты x', y', и z все разделены на w':
x" = x' / w'
y" = y' / w'
z" = z' / w'
w" = w' / w' = 1
Это разделение по w' обеспечивает перспективу в трехмерном пространстве. Если w' равен 1, то перспектива не возникает.
Повороты в трехмерном пространстве могут быть довольно сложными, но простейшие повороты находятся вокруг осей X, Y и Z. Поворот угловой α вокруг оси X — это матрица:
| 1 0 0 0 | | 0 cos(α) sin(α) 0 | | 0 –sin(α) cos(α) 0 | | 0 0 0 1 |
Значения X остаются неизменными при выполнении этого преобразования. Поворот вокруг оси Y оставляет значения Y без изменений:
| cos(α) 0 –sin(α) 0 | | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 0 1 |
Поворот вокруг оси Z совпадает с трехмерной графикой:
| cos(α) sin(α) 0 0 | | –sin(α) cos(α) 0 0 | | 0 0 1 0 | | 0 0 0 1 |
Направление поворота подразумевается рукой системы координат. Это левая система, поэтому если вы указываете пальцем левой руки на увеличение значений для определенной оси — справа для поворота вокруг оси X, вниз для поворота вокруг оси Y и к вам для поворота вокруг оси Z , то кривая других пальцев указывает направление поворота для положительных углов.
SKMatrix44 имеет обобщенные статические CreateRotation и CreateRotationDegrees методы, позволяющие указать ось, вокруг которой происходит поворот:
public static SKMatrix44 CreateRotationDegrees (Single x, Single y, Single z, Single degrees)
Для поворота вокруг оси X задайте для первых трех аргументов значение 1, 0, 0. Для поворота вокруг оси Y задайте для них значение 0, 1, 0 и для поворота вокруг оси Z, задайте для них значение 0, 0, 1.
Четвертый столбец 4-к-4 предназначен для перспективы. Нет SKMatrix44 методов для создания преобразований перспективы, но вы можете создать его самостоятельно с помощью следующего кода:
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
Причина имени depth аргумента будет очевидна в ближайшее время. Этот код создает матрицу:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 -1/depth | | 0 0 0 1 |
Формулы преобразования приводят к следующему вычислению w':
w' = –z / depth + 1
Это позволяет уменьшить координаты X и Y, если значения Z меньше нуля (концептуально за плоскости XY) и увеличить координаты X и Y для положительных значений Z. Когда координата depthZ равна нулю, а координаты становятся бесконечными. Трехмерные графические системы создаются вокруг метафоры камеры, а depth значение здесь представляет расстояние камеры от источника системы координат. Если графический объект имеет координату Z, которая является depth единицами из источника, она концептуально касается объектива камеры и становится бесконечно большой.
Помните, что вы, вероятно, будете использовать это perspectiveMatrix значение в сочетании с матрицами поворота. Если вращаемый графический объект имеет координаты X или Y больше depth, то поворот этого объекта в трехмерном пространстве, скорее всего, будет включать координаты Z больше, чем depth. Это необходимо избежать! При создании perspectiveMatrix необходимо задать depth достаточно большое значение для всех координат в графическом объекте независимо от того, как он поворачивается. Это гарантирует, что никакого деления на ноль никогда не существует.
Объединение трехмерных поворотов и перспективы требует умножения 4 на 4 матрицы вместе. Для этого SKMatrix44 определяет методы объединения. Если A и B являются SKMatrix44 объектами, следующий код задает A равно A × B:
A.PostConcat(B);
Если матрица преобразования 4–4 используется в 2D-графической системе, она применяется к 2D-объектам. Эти объекты являются неструктурированными, и предполагается, что координаты Z равны нулю. Умножение преобразования немного проще, чем показанное ранее преобразование:
| M11 M12 M13 M14 |
| x y 0 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Это значение 0 для z приводит к формулам преобразования, которые не включают ячейки в третьей строке матрицы:
x' = M11·x + M21·y + M41
y' = M12·x + M22·y + M42
z' = M13·x + M23·y + M43
w' = M14·x + M24·y + M44
Кроме того, координата Z здесь не имеет значения. Если трехмерный объект отображается в трехмерной графической системе, он свернут в двухмерный объект, игнорируя значения координат Z. Формулы преобразования на самом деле являются двумя:
x" = x' / w'
y" = y' / w'
Это означает, что третью строку и третий столбец матрицы 4-4 можно игнорировать.
Но если это так, почему матрица 4-к-4 даже необходима в первую очередь?
Хотя третья строка и третий столбец 4-к-4 не имеют значения для двухмерных преобразований, третья строка и столбец играют роль до этого, когда различные SKMatrix44 значения умножаются вместе. Например, предположим, что вы умножаете поворот вокруг оси Y с преобразованием перспективы:
| cos(α) 0 –sin(α) 0 | | 1 0 0 0 | | cos(α) 0 –sin(α) sin(α)/depth | | 0 1 0 0 | × | 0 1 0 0 | = | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 1 -1/depth | | sin(α) 0 cos(α) -cos(α)/depth | | 0 0 0 1 | | 0 0 0 1 | | 0 0 0 1 |
В продукте ячейка M14 теперь содержит значение перспективы. Если вы хотите применить эту матрицу к объектам 2D, третья строка и столбец удаляются, чтобы преобразовать ее в матрицу с 3 по 3:
| cos(α) 0 sin(α)/depth | | 0 1 0 | | 0 0 1 |
Теперь его можно использовать для преобразования 2D-точки:
| cos(α) 0 sin(α)/depth |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| 0 0 1 |
Формулы преобразования:
x' = cos(α)·x
y' = y
z' = (sin(α)/depth)·x + 1
Теперь разделите все на z':
x" = cos(α)·x / ((sin(α)/depth)·x + 1)
y" = y / ((sin(α)/depth)·x + 1)
Когда 2D-объекты поворачиваются с положительным углом вокруг оси Y, то положительные значения X отступают на фон, а отрицательные значения X приходят на передний план. Значения X, кажется, приближаются к оси Y (которая управляется значением косинуса), так как координаты от оси Y становятся меньше или больше, когда они перемещаются дальше от средства просмотра или ближе к средству просмотра.
При использовании SKMatrix44выполните все трехмерные операции поворота и перспективы путем умножения различных SKMatrix44 значений. Затем можно извлечь двухмерную матрицу 3-к-3 из матрицы 4-к-4 с помощью Matrix свойства SKMatrix44 класса. Это свойство возвращает знакомое SKMatrix значение.
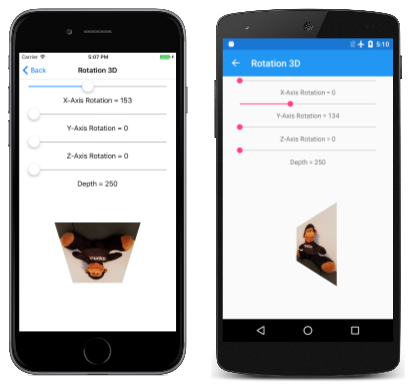
Страница поворота 3D позволяет экспериментировать с трехмерной сменой. Файл Rotation3DPage.xaml создает четыре ползунка, чтобы задать поворот вокруг осей X, Y и Z, а также задать значение глубины:
<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
x:Class="SkiaSharpFormsDemos.Transforms.Rotation3DPage"
Title="Rotation 3D">
<Grid>
<Grid.RowDefinitions>
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="*" />
</Grid.RowDefinitions>
<Grid.Resources>
<ResourceDictionary>
<Style TargetType="Label">
<Setter Property="HorizontalTextAlignment" Value="Center" />
</Style>
<Style TargetType="Slider">
<Setter Property="Margin" Value="20, 0" />
<Setter Property="Maximum" Value="360" />
</Style>
</ResourceDictionary>
</Grid.Resources>
<Slider x:Name="xRotateSlider"
Grid.Row="0"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference xRotateSlider},
Path=Value,
StringFormat='X-Axis Rotation = {0:F0}'}"
Grid.Row="1" />
<Slider x:Name="yRotateSlider"
Grid.Row="2"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference yRotateSlider},
Path=Value,
StringFormat='Y-Axis Rotation = {0:F0}'}"
Grid.Row="3" />
<Slider x:Name="zRotateSlider"
Grid.Row="4"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference zRotateSlider},
Path=Value,
StringFormat='Z-Axis Rotation = {0:F0}'}"
Grid.Row="5" />
<Slider x:Name="depthSlider"
Grid.Row="6"
Maximum="2500"
Minimum="250"
ValueChanged="OnSliderValueChanged" />
<Label Grid.Row="7"
Text="{Binding Source={x:Reference depthSlider},
Path=Value,
StringFormat='Depth = {0:F0}'}" />
<skia:SKCanvasView x:Name="canvasView"
Grid.Row="8"
PaintSurface="OnCanvasViewPaintSurface" />
</Grid>
</ContentPage>
Обратите внимание, что инициализировано depthSlider со значением Minimum 250. Это означает, что 2D-объект, вращаемый здесь, имеет координаты X и Y, ограниченные кругом, определенным радиусом 250 пикселей вокруг источника. Любой поворот этого объекта в трехмерном пространстве всегда приводит к значению координат менее 250.
Файл Rotation3DPage.cs программной части загружается в растровом рисунке, который составляет 300 пикселей:
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
...
}
Если трехмерный преобразование сосредоточено на этом растровом рисунке, координаты X и Y находятся в диапазоне от –150 до 150, а угловые — 212 пикселей от центра, поэтому все находится в радиусе 250 пикселей.
Обработчик PaintSurface создает SKMatrix44 объекты на основе ползунка и умножает их вместе с помощью PostConcat. Значение SKMatrix , извлеченное из конечного SKMatrix44 объекта, окружено преобразованиями, чтобы центрировать поворот в центре экрана:
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Use 3D matrix for 3D rotations and perspective
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, (float)xRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, (float)yRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, (float)zRotateSlider.Value));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / (float)depthSlider.Value;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the bitmap
canvas.SetMatrix(matrix);
float xBitmap = xCenter - bitmap.Width / 2;
float yBitmap = yCenter - bitmap.Height / 2;
canvas.DrawBitmap(bitmap, xBitmap, yBitmap);
}
}
При эксперименте с четвертым ползунок вы заметите, что различные параметры глубины не перемещают объект дальше от средства просмотра, а вместо этого изменяют степень эффекта перспективы:
Анимированный поворот 3D также используется SKMatrix44 для анимации текстовой строки в трехмерном пространстве. Объект, textPaint заданный в качестве поля, используется в конструкторе для определения границ текста:
public class AnimatedRotation3DPage : ContentPage
{
SKCanvasView canvasView;
float xRotationDegrees, yRotationDegrees, zRotationDegrees;
string text = "SkiaSharp";
SKPaint textPaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Black,
TextSize = 100,
StrokeWidth = 3,
};
SKRect textBounds;
public AnimatedRotation3DPage()
{
Title = "Animated Rotation 3D";
canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
// Measure the text
textPaint.MeasureText(text, ref textBounds);
}
...
}
Переопределение OnAppearing определяет триAnimationXamarin.Formsобъекта для анимации xRotationDegreesyRotationDegreesполей и zRotationDegrees полей с разными скоростями. Обратите внимание, что для периодов этих анимаций заданы простые числа (5 секунд, 7 секунд и 11 секунд), поэтому общая комбинация повторяется только каждые 385 секунд или более 10 минут:
public class AnimatedRotation3DPage : ContentPage
{
...
protected override void OnAppearing()
{
base.OnAppearing();
new Animation((value) => xRotationDegrees = 360 * (float)value).
Commit(this, "xRotationAnimation", length: 5000, repeat: () => true);
new Animation((value) => yRotationDegrees = 360 * (float)value).
Commit(this, "yRotationAnimation", length: 7000, repeat: () => true);
new Animation((value) =>
{
zRotationDegrees = 360 * (float)value;
canvasView.InvalidateSurface();
}).Commit(this, "zRotationAnimation", length: 11000, repeat: () => true);
}
protected override void OnDisappearing()
{
base.OnDisappearing();
this.AbortAnimation("xRotationAnimation");
this.AbortAnimation("yRotationAnimation");
this.AbortAnimation("zRotationAnimation");
}
...
}
Как и в предыдущей программе, PaintCanvas обработчик создает SKMatrix44 значения для поворота и перспективы и умножает их вместе:
public class AnimatedRotation3DPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Scale so text fits
float scale = Math.Min(info.Width / textBounds.Width,
info.Height / textBounds.Height);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(scale, scale));
// Calculate composite 3D transforms
float depth = 0.75f * scale * textBounds.Width;
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, xRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, yRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, zRotationDegrees));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the text
canvas.SetMatrix(matrix);
float xText = xCenter - textBounds.MidX;
float yText = yCenter - textBounds.MidY;
canvas.DrawText(text, xText, yText, textPaint);
}
}
Этот трехмерный поворот окружен несколькими 2D-преобразованиями для перемещения центра поворота в центр экрана и масштабирования размера текстовой строки таким образом, чтобы она была той же шириной, что и экран: