Три способа нарисовать дугу

Узнайте, как использовать SkiaSharp для определения дуг тремя способами

Дуга — это кривая по окружности многоточия, например округленные части этого знака бесконечности:

Несмотря на простоту этого определения, нет способа определить функцию рисования дуги, которая удовлетворяет каждой необходимости, и, следовательно, нет консенсуса среди графических систем лучшего способа рисования дуги. По этой причине SKPath класс не ограничивает себя только одним подходом.

SKPath определяет AddArc метод, пять разных ArcTo методов и два относительных RArcTo метода. Эти методы делятся на три категории, представляющие три очень разных подхода к указанию дуги. Какой из них вы используете, зависит от информации, доступной для определения дуги, и того, как эта дуга вписывается в другую графику, которую вы рисуете.

Угловая дуга

Для подхода угловой дуги к рисованию дуги требуется указать прямоугольник, ограничивающий многоточие. Дуга по окружности этого эллипса обозначается углами от центра эллипса, которые указывают на начало дуги и ее длины. Два разных метода рисуют угловые дуги. AddArc Это метод и ArcTo метод:

public void AddArc (SKRect oval, Single startAngle, Single sweepAngle)

public void ArcTo (SKRect oval, Single startAngle, Single sweepAngle, Boolean forceMoveTo)

Эти методы идентичны методам Android AddArc и [ArcTo]xref:Android.Graphics.Path.ArcTo*.. Метод iOS AddArc аналогичен, но ограничен дугами по окружности круга, а не обобщенным к многоточию.

Оба метода начинаются со SKRect значения, определяющего расположение и размер многоточия:

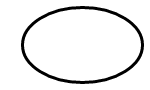
Дуга является частью окружности этого многоточия.

Аргумент startAngle является по часовой стрелке в градусах относительно горизонтальной линии, нарисованной от центра многоточия справа. Аргумент sweepAngle относится к аргументу startAngle. Ниже приведены startAngle значения sweepAngle 60 градусов и 100 градусов соответственно:

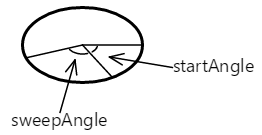
Дуга начинается с угла начала. Его длина регулируется углом сверток. Дуга показана здесь красным цветом:

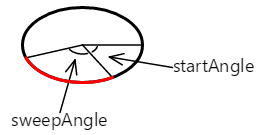
Кривая, добавленная к пути с AddArc помощью метода, ArcTo просто является частью окружности эллипса:

sweepAngle Аргументы startAngle могут быть отрицательными: дуга по часовой стрелке для положительных значений sweepAngle и счетчиков по часовой стрелке для отрицательных значений.

AddArc Однако не определяет закрытый контур. При вызове LineTo после AddArc, линия рисуется с конца дуги до точки в методе LineTo , и то же самое имеет значение true ArcTo.

AddArc автоматически запускает новый контур и функционально эквивалентен вызову ArcTo с окончательным аргументом true:

path.ArcTo (oval, startAngle, sweepAngle, true);

Этот последний аргумент вызывается forceMoveTo, и он фактически вызывает MoveTo вызов в начале дуги. Это начинает новый контур. Это не так с последним аргументом false:

path.ArcTo (oval, startAngle, sweepAngle, false);

Эта версия ArcTo рисует линию от текущей позиции к началу дуги. Это означает, что дуга может быть где-то в середине более крупного контура.

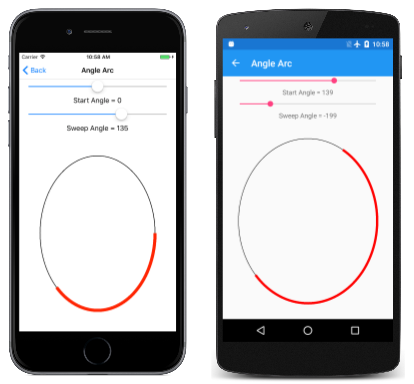
Страница "Угол дуги" позволяет использовать два ползунка, чтобы указать угол начала и очистки. XAML-файл создает экземпляры двух Slider элементов и объекта SKCanvasView. Обработчик PaintCanvas в файле AngleArcPage.xaml.cs рисует овал и дугу, используя два SKPaint объекта, определенных как поля:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    SKRect rect = new SKRect(100, 100, info.Width - 100, info.Height - 100);
    float startAngle = (float)startAngleSlider.Value;
    float sweepAngle = (float)sweepAngleSlider.Value;

    canvas.DrawOval(rect, outlinePaint);

    using (SKPath path = new SKPath())
    {
        path.AddArc(rect, startAngle, sweepAngle);
        canvas.DrawPath(path, arcPaint);
    }
}

Как видно, угол начала и угол сверток могут принимать отрицательные значения:

Этот подход к созданию дуги алгоритмически прост, и легко наследовать формулы параметрики, описывающие дугу. Зная размер и расположение многоточия, а также угол начала и развертки, начальные и конечные точки дуги можно вычислить с помощью простой тригонометрии:

x = oval.MidX + (oval.Width / 2) * cos(angle)

y = oval.MidY + (oval.Height / 2) * sin(angle)

Значение angle равно или startAngle startAngle + sweepAngle.

Использование двух углов для определения дуги лучше всего подходит для случаев, когда вы знаете угловую длину дуги, которую вы хотите нарисовать, например, для создания круговой диаграммы. На странице "Взрывная круговая диаграмма " показано это. Класс ExplodedPieChartPage использует внутренний класс для определения некоторых сфабрикованных данных и цветов:

class ChartData
{
    public ChartData(int value, SKColor color)
    {
        Value = value;
        Color = color;
    }

    public int Value { private set; get; }

    public SKColor Color { private set; get; }
}

ChartData[] chartData =
{
    new ChartData(45, SKColors.Red),
    new ChartData(13, SKColors.Green),
    new ChartData(27, SKColors.Blue),
    new ChartData(19, SKColors.Magenta),
    new ChartData(40, SKColors.Cyan),
    new ChartData(22, SKColors.Brown),
    new ChartData(29, SKColors.Gray)
};

Обработчик PaintSurface сначала выполняет циклы по элементам, чтобы вычислить totalValues число. Из этого он может определить размер каждого элемента в виде доли суммы и преобразовать его в угол:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    int totalValues = 0;

    foreach (ChartData item in chartData)
    {
        totalValues += item.Value;
    }

    SKPoint center = new SKPoint(info.Width / 2, info.Height / 2);
    float explodeOffset = 50;
    float radius = Math.Min(info.Width / 2, info.Height / 2) - 2 * explodeOffset;
    SKRect rect = new SKRect(center.X - radius, center.Y - radius,
                             center.X + radius, center.Y + radius);

    float startAngle = 0;

    foreach (ChartData item in chartData)
    {
        float sweepAngle = 360f * item.Value / totalValues;

        using (SKPath path = new SKPath())
        using (SKPaint fillPaint = new SKPaint())
        using (SKPaint outlinePaint = new SKPaint())
        {
            path.MoveTo(center);
            path.ArcTo(rect, startAngle, sweepAngle, false);
            path.Close();

            fillPaint.Style = SKPaintStyle.Fill;
            fillPaint.Color = item.Color;

            outlinePaint.Style = SKPaintStyle.Stroke;
            outlinePaint.StrokeWidth = 5;
            outlinePaint.Color = SKColors.Black;

            // Calculate "explode" transform
            float angle = startAngle + 0.5f * sweepAngle;
            float x = explodeOffset * (float)Math.Cos(Math.PI * angle / 180);
            float y = explodeOffset * (float)Math.Sin(Math.PI * angle / 180);

            canvas.Save();
            canvas.Translate(x, y);

            // Fill and stroke the path
            canvas.DrawPath(path, fillPaint);
            canvas.DrawPath(path, outlinePaint);
            canvas.Restore();
        }

        startAngle += sweepAngle;
    }
}

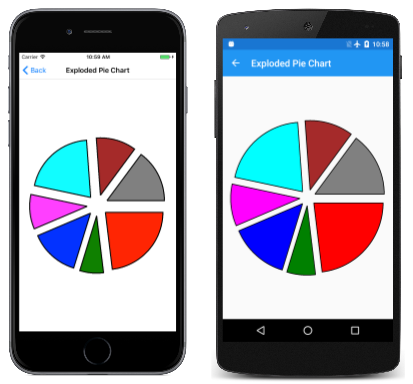
Для каждого кругового среза создается новый SKPath объект. Путь состоит из линии из центра, а затем ArcTo для рисования дуги и другой линии обратно к центру Close результатов вызова. В этой программе отображаются "взрывные" круговой срезы, перемещая их все из центра на 50 пикселей. Для этой задачи требуется вектор в направлении средней точки угла развертки для каждого среза:

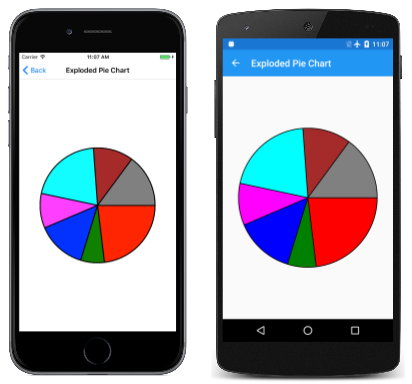
Чтобы увидеть, как выглядит без "взрыва", просто закомментируйте Translate звонок:

Тангент арка

Второй тип дуги, поддерживаемой SKPath тангенсной дугой, так называемый, потому что дуга является окружностью круга, который тангенс к двум подключенным линиям.

Тангенс дуги добавляется в путь с вызовом ArcTo метода с двумя SKPoint параметрами или ArcTo перегрузкой с отдельными Single параметрами для точек:

public void ArcTo (SKPoint point1, SKPoint point2, Single radius)

public void ArcTo (Single x1, Single y1, Single x2, Single y2, Single radius)

Этот ArcTo метод аналогичен функции PostScript arct (страница 532) и методу iOS AddArcToPoint .

Метод ArcTo состоит из трех точек:

• Текущая точка контура или точка (0, 0), если MoveTo не была вызвана
• Первый аргумент точки метода ArcTo , называемый точкой угла
• Второй аргумент ArcToточки, на который называется целевая точка:

Эти три точки определяют две подключенные линии:

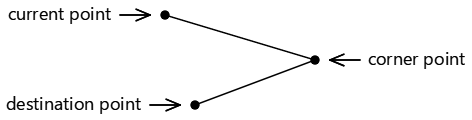
Если три точки являются линейными - то есть, если они лежат на одной прямой линии - ни одна дуга не будет нарисована.

Метод ArcTo также включает radius параметр. Это определяет радиус круга:

Тангентная дуга не обобщена для многоточия.

Если две линии встречаются в любом углу, этот круг можно вставить между этими линиями, чтобы они были тангенсными для обеих строк:

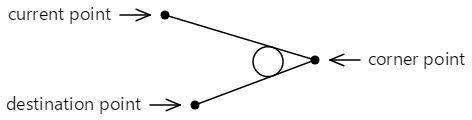
Кривая, добавляемая к контуру, не касается ни одного из точек, указанных в методе ArcTo . Он состоит из прямой линии от текущей точки до первой тангенсной точки, и дуги, которая заканчивается во второй тангенсной точке, показанной здесь в красном цвете:

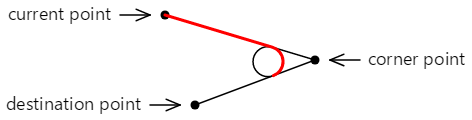
Вот последняя прямая линия и дуга, которая добавляется в контур:

Контур можно продолжить со второй тангенсной точки.

Страница Tangent Arc позволяет экспериментировать с тангенсной дугой. Это первый из нескольких страниц, производных от InteractivePage, который определяет несколько удобных SKPaint объектов и выполняет TouchPoint обработку:

public class InteractivePage : ContentPage
{
    protected SKCanvasView baseCanvasView;
    protected TouchPoint[] touchPoints;

    protected SKPaint strokePaint = new SKPaint
    {
        Style = SKPaintStyle.Stroke,
        Color = SKColors.Black,
        StrokeWidth = 3
    };

    protected SKPaint redStrokePaint = new SKPaint
    {
        Style = SKPaintStyle.Stroke,
        Color = SKColors.Red,
        StrokeWidth = 15
    };

    protected SKPaint dottedStrokePaint = new SKPaint
    {
        Style = SKPaintStyle.Stroke,
        Color = SKColors.Black,
        StrokeWidth = 3,
        PathEffect = SKPathEffect.CreateDash(new float[] { 7, 7 }, 0)
    };

    protected void OnTouchEffectAction(object sender, TouchActionEventArgs args)
    {
        bool touchPointMoved = false;

        foreach (TouchPoint touchPoint in touchPoints)
        {
            float scale = baseCanvasView.CanvasSize.Width / (float)baseCanvasView.Width;
            SKPoint point = new SKPoint(scale * (float)args.Location.X,
                                        scale * (float)args.Location.Y);
            touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, point);
        }

        if (touchPointMoved)
        {
            baseCanvasView.InvalidateSurface();
        }
    }
}

Класс TangentArcPage является производным от InteractivePage. Конструктор в файле TangentArcPage.xaml.cs отвечает за создание экземпляра и инициализацию touchPoints массива и настройку baseCanvasView (вInteractivePage) объектаSKCanvasView, созданного в файле TangentArcPage.xaml:

public partial class TangentArcPage : InteractivePage
{
    public TangentArcPage()
    {
        touchPoints = new TouchPoint[3];

        for (int i = 0; i < 3; i++)
        {
            TouchPoint touchPoint = new TouchPoint
            {
                Center = new SKPoint(i == 0 ? 100 : 500,
                                     i != 2 ? 100 : 500)
            };
            touchPoints[i] = touchPoint;
        }

        InitializeComponent();

        baseCanvasView = canvasView;
        radiusSlider.Value = 100;
    }

    void sliderValueChanged(object sender, ValueChangedEventArgs args)
    {
        if (canvasView != null)
        {
            canvasView.InvalidateSurface();
        }
    }
    ...
}

Обработчик PaintSurface использует ArcTo метод для рисования дуги на основе точек касания и а Slider, а также алгоритмически вычисляет круг, на основе угла:

public partial class TangentArcPage : InteractivePage
{
    ...
    void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
    {
        SKImageInfo info = args.Info;
        SKSurface surface = args.Surface;
        SKCanvas canvas = surface.Canvas;

        canvas.Clear();

        // Draw the two lines that meet at an angle
        using (SKPath path = new SKPath())
        {
            path.MoveTo(touchPoints[0].Center);
            path.LineTo(touchPoints[1].Center);
            path.LineTo(touchPoints[2].Center);
            canvas.DrawPath(path, dottedStrokePaint);
        }

        // Draw the circle that the arc wraps around
        float radius = (float)radiusSlider.Value;

        SKPoint v1 = Normalize(touchPoints[0].Center - touchPoints[1].Center);
        SKPoint v2 = Normalize(touchPoints[2].Center - touchPoints[1].Center);

        double dotProduct = v1.X * v2.X + v1.Y * v2.Y;
        double angleBetween = Math.Acos(dotProduct);
        float hypotenuse = radius / (float)Math.Sin(angleBetween / 2);
        SKPoint vMid = Normalize(new SKPoint((v1.X + v2.X) / 2, (v1.Y + v2.Y) / 2));
        SKPoint center = new SKPoint(touchPoints[1].Center.X + vMid.X * hypotenuse,
                                     touchPoints[1].Center.Y + vMid.Y * hypotenuse);

        canvas.DrawCircle(center.X, center.Y, radius, this.strokePaint);

        // Draw the tangent arc
        using (SKPath path = new SKPath())
        {
            path.MoveTo(touchPoints[0].Center);
            path.ArcTo(touchPoints[1].Center, touchPoints[2].Center, radius);
            canvas.DrawPath(path, redStrokePaint);
        }

        foreach (TouchPoint touchPoint in touchPoints)
        {
            touchPoint.Paint(canvas);
        }
    }

    // Vector methods
    SKPoint Normalize(SKPoint v)
    {
        float magnitude = Magnitude(v);
        return new SKPoint(v.X / magnitude, v.Y / magnitude);
    }

    float Magnitude(SKPoint v)
    {
        return (float)Math.Sqrt(v.X * v.X + v.Y * v.Y);
    }
}

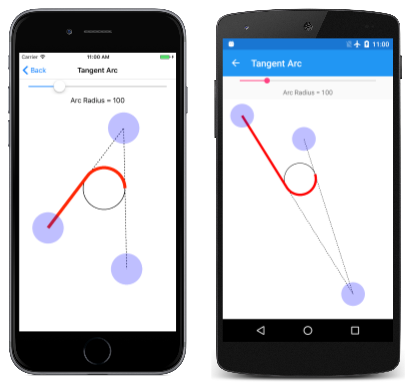
Ниже приведена страница Tangent Arc:

Тангенс дуги идеально подходит для создания округлых углов, таких как округленный прямоугольник. Так как SKPath уже включает AddRoundedRect метод, страница округленного хептагона демонстрирует, как использовать ArcTo для округления углов семистороннего многоугольника. (Код обобщен для любого регулярного многоугольника.)

Обработчик PaintSurface RoundedHeptagonPage класса содержит один for цикл для вычисления координат семи вершин гептагона, а второй — для вычисления середины семи сторон от этих вершин. Затем эти средние точки используются для создания пути:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    float cornerRadius = 100;
    int numVertices = 7;
    float radius = 0.45f * Math.Min(info.Width, info.Height);

    SKPoint[] vertices = new SKPoint[numVertices];
    SKPoint[] midPoints = new SKPoint[numVertices];

    double vertexAngle = -0.5f * Math.PI;       // straight up

    // Coordinates of the vertices of the polygon
    for (int vertex = 0; vertex < numVertices; vertex++)
    {
        vertices[vertex] = new SKPoint(radius * (float)Math.Cos(vertexAngle),
                                       radius * (float)Math.Sin(vertexAngle));
        vertexAngle += 2 * Math.PI / numVertices;
    }

    // Coordinates of the midpoints of the sides connecting the vertices
    for (int vertex = 0; vertex < numVertices; vertex++)
    {
        int prevVertex = (vertex + numVertices - 1) % numVertices;
        midPoints[vertex] = new SKPoint((vertices[prevVertex].X + vertices[vertex].X) / 2,
                                        (vertices[prevVertex].Y + vertices[vertex].Y) / 2);
    }

    // Create the path
    using (SKPath path = new SKPath())
    {
        // Begin at the first midpoint
        path.MoveTo(midPoints[0]);

        for (int vertex = 0; vertex < numVertices; vertex++)
        {
            SKPoint nextMidPoint = midPoints[(vertex + 1) % numVertices];

            // Draws a line from the current point, and then the arc
            path.ArcTo(vertices[vertex], nextMidPoint, cornerRadius);

            // Connect the arc with the next midpoint
            path.LineTo(nextMidPoint);
        }
        path.Close();

        // Render the path in the center of the screen
        using (SKPaint paint = new SKPaint())
        {
            paint.Style = SKPaintStyle.Stroke;
            paint.Color = SKColors.Blue;
            paint.StrokeWidth = 10;

            canvas.Translate(info.Width / 2, info.Height / 2);
            canvas.DrawPath(path, paint);
        }
    }
}

Вот работающая программа:

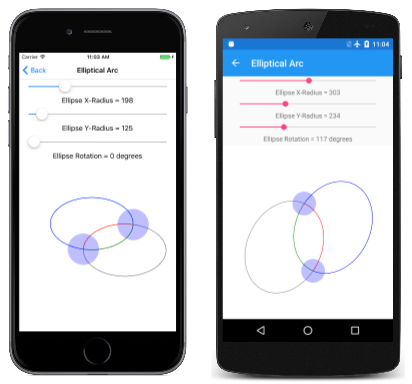
Эллиптическая арка

Эллиптическая дуга добавляется в путь с вызовом ArcTo метода с двумя SKPoint параметрами или ArcTo перегрузкой с отдельными координатами X и Y:

public void ArcTo (SKPoint r, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, SKPoint xy)

public void ArcTo (Single rx, Single ry, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, Single x, Single y)

Эллиптическая дуга соответствует эллиптической дуге, включенной в масштабируемую векторную графику (SVG) и класс универсальная платформа WindowsArcSegment.

Эти ArcTo методы рисуют дугу между двумя точками, которые являются текущей точкой контура, и последним параметром метода (xyпараметром ArcTo или отдельными x и y параметрами):

Первый параметр ArcTo точки для метода (rили rx ry) не является точкой вообще, но вместо этого указывает горизонтальную и вертикальную радию многоточия;

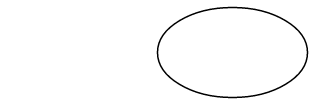
Параметр xAxisRotate — это число часовых градусов для поворота этого многоточия:

Если это наклонное многоточие затем позиционируется так, чтобы он касался двух точек, точки связаны двумя разными дугами:

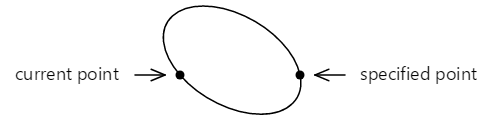
Эти две дуги можно различать двумя способами: верхняя дуга больше нижней дуги, а по мере того как дуга рисуется слева направо, верхняя дуга рисуется в часовом направлении, а нижняя дуга рисуется в направлении по часовой стрелке.

Также можно вписать многоточие между двумя точками другим способом:

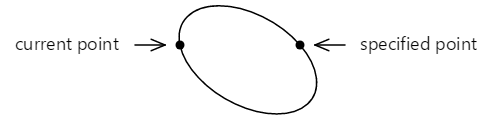
Теперь есть меньшая дуга на вершине, которая рисуется по часовой стрелке, и большая дуга на нижней части, которая рисуется по часовой стрелке.

Таким образом, эти две точки могут быть соединены дугой, определенной наклонной многоточием в общей сложности четыре способа:

Эти четыре дуги отличаются четырьмя сочетаниями аргументов SKPathArcSize SKPathDirection типа перечисления и ArcTo метода:

• red: SKPathArcSize.Large и SKPathDirection.Clockwise
• зеленый: SKPathArcSize.Small и SKPathDirection.Clockwise
• blue: SKPathArcSize.Small и SKPathDirection.CounterClockwise
• magenta: SKPathArcSize.Large и SKPathDirection.CounterClockwise

Если многоточие наклона недостаточно большое, чтобы поместиться между двумя точками, то оно равномерно масштабируется, пока не будет достаточно большим. Только две уникальные дуги соединяют две точки в этом случае. Их можно отличить с параметром SKPathDirection .

Хотя этот подход к определению дуги звучит сложно при первой встрече, это единственный подход, который позволяет определить дугу с повернутым многоточием, и это часто самый простой подход, когда необходимо интегрировать дуги с другими частями контура.

Страница Elliptical Arc позволяет интерактивно задать две точки, а также размер и поворот многоточия. Класс EllipticalArcPage является производным от InteractivePage, а PaintSurface обработчик в файле кода EllipticalArcPage.xaml.cs выполняет рисование четырех дуг:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    using (SKPath path = new SKPath())
    {
        int colorIndex = 0;
        SKPoint ellipseSize = new SKPoint((float)xRadiusSlider.Value,
                                          (float)yRadiusSlider.Value);
        float rotation = (float)rotationSlider.Value;

        foreach (SKPathArcSize arcSize in Enum.GetValues(typeof(SKPathArcSize)))
            foreach (SKPathDirection direction in Enum.GetValues(typeof(SKPathDirection)))
            {
                path.MoveTo(touchPoints[0].Center);
                path.ArcTo(ellipseSize, rotation,
                           arcSize, direction,
                           touchPoints[1].Center);

                strokePaint.Color = colors[colorIndex++];
                canvas.DrawPath(path, strokePaint);
                path.Reset();
            }
    }

    foreach (TouchPoint touchPoint in touchPoints)
    {
        touchPoint.Paint(canvas);
    }
}

Здесь выполняется:

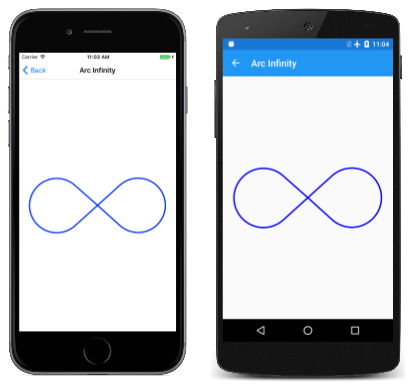
На странице Arc Infinity используется эллиптическая дуга для рисования знака бесконечности . Знак бесконечности основан на двух кругах с радиями 100 единиц, разделенных 100 единицами:

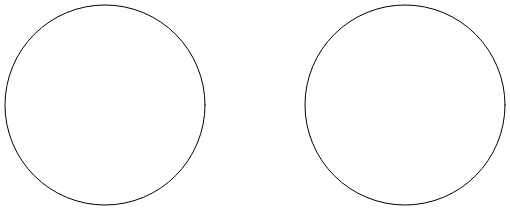
Две линии, пересекающие друг друга, касаются обоих кругов:

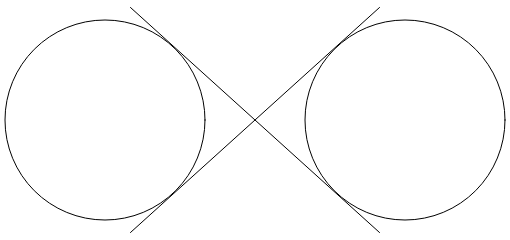
Знак бесконечности — это сочетание частей этих кругов и двух линий. Чтобы использовать эллиптические дуги для рисования знака бесконечности, координаты, в которых две линии тангенты к кругам, должны быть определены.

Создайте правый прямоугольник в одном из кругов:

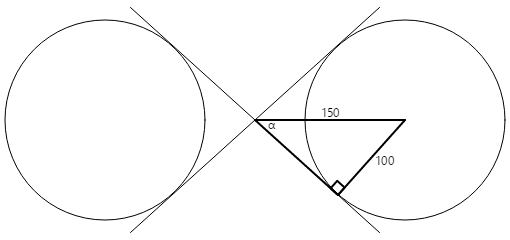
Радиус круга составляет 100 единиц, а гипотенуз треугольника составляет 150 единиц, поэтому угол α является арксин (инверсный синус) 100, разделенный на 150 или 41,8 градуса. Длина другой стороны треугольника составляет 150 раз косинус 41,8 градуса, или 112, который также можно вычислить теоремом Пифагора.

Затем координаты точки тангенса можно вычислить с помощью следующих сведений:

x = 112·cos(41.8) = 83

y = 112·sin(41.8) = 75

Четыре тангенсные точки являются все, что необходимо для рисования бесконечного знака, центрированного на точке (0, 0) с кругом радии 100:

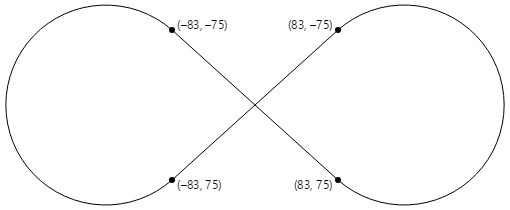
Обработчик PaintSurface в ArcInfinityPage классе размещает знак бесконечности, чтобы точка (0, 0) располагалась в центре страницы и масштабирует путь к размеру экрана:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    using (SKPath path = new SKPath())
    {
        path.LineTo(83, 75);
        path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.CounterClockwise, 83, -75);
        path.LineTo(-83, 75);
        path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.Clockwise, -83, -75);
        path.Close();

        // Use path.TightBounds for coordinates without control points
        SKRect pathBounds = path.Bounds;

        canvas.Translate(info.Width / 2, info.Height / 2);
        canvas.Scale(Math.Min(info.Width / pathBounds.Width,
                              info.Height / pathBounds.Height));

        using (SKPaint paint = new SKPaint())
        {
            paint.Style = SKPaintStyle.Stroke;
            paint.Color = SKColors.Blue;
            paint.StrokeWidth = 5;

            canvas.DrawPath(path, paint);
        }
    }
}

Код использует Bounds свойство SKPath для определения измерений бесконечности синуса, чтобы масштабировать его до размера холста:

Результат кажется немного маленьким, что предполагает, что Bounds свойство SKPath сообщает размер больше, чем путь.

Внутри, Skia приблизит дугу с помощью нескольких квадратных кривых Bézier. Эти кривые (как вы увидите в следующем разделе) содержат контрольные точки, которые управляют нарисовкой кривой, но не являются частью отрисованной кривой. Свойство Bounds включает эти контрольные точки.

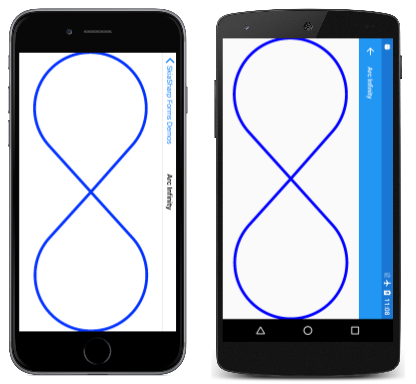
Чтобы получить более жесткое соответствие, используйте TightBounds свойство, которое исключает контрольные точки. Ниже приведена программа, выполняемая в альбомном режиме, и с помощью TightBounds свойства для получения границ пути:

Хотя соединения между дуги и прямыми линиями математически гладки, изменение от дуги к прямой линии может показаться немного резко. Более лучший знак бесконечности представлен в следующей статье о трех типах кривых Bézier.

Связанные ссылки

• API SkiaSharp