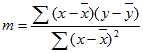Метод WorksheetFunction.LinEst (Excel)

Статья
04/07/2023

Вычисляет статистику для линии с помощью метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом соответствует вашим данным, и возвращает массив, описывающий линию. Так как эта функция возвращает массив значений, его необходимо ввести в виде формулы массива.

Синтаксис

expression. LinEst (Arg1, Arg2, Arg3, Arg4)

Выражение Переменная, представляющая объект WorksheetFunction .

Параметры

Имя	Обязательный или необязательный	Тип данных	Описание
Arg1	Обязательный	Variant	Known_y — набор значений y, которые вы уже знаете в связи y = mx + b.
Arg2	Необязательный	Variant	Known_x — необязательный набор значений x, которые, возможно, уже известны в связи y = mx + b.
Arg3	Необязательный	Variant	Const — логическое значение, указывающее, следует ли принудительно принудить константу b к 0.
Arg4	Необязательный	Variant	Stats — логическое значение, указывающее, следует ли возвращать дополнительную статистику регрессии.

Возвращаемое значение

Variant

Примечания

Уравнение для строки — y = mx + b или y = m1x1 + m2x2 + ... + b (при наличии нескольких диапазонов значений x), где зависимое значение y является функцией независимых значений x. Значения m являются коэффициентами, соответствующими каждому значению x, а b — константным значением. Обратите внимание, что y, x и m могут быть векторами. Массив, возвращающий LinEst , имеет значение {mn,mn-1,...,m1,b}. LinEst также может возвращать дополнительную статистику регрессии.

Если массив known_y находится в одном столбце, каждый столбец known_x интерпретируется как отдельная переменная.

Если массив known_y находится в одной строке, каждая строка known_x интерпретируется как отдельная переменная.

Массив known_x может включать один или несколько наборов переменных. Если используется только одна переменная, known_y и known_x могут быть диапазонами любой формы, если они имеют равные размеры. Если используется несколько переменных, known_y должны быть вектором (то есть диапазоном высотой одной строки или шириной одного столбца).

Если known_x опущен, предполагается {1,2,3,...} , что массив имеет тот же размер, что и known_y.

Если параметр const имеет значение True или опущен, b вычисляется обычно.
Если const имеет значение False, значение b равно 0, а значения m корректируются в соответствии с .y = mx
Если stats имеет значение True, LinEst возвращает дополнительную статистику регрессии, поэтому возвращаемый массив имеет значение {mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r2,sey;F,df;ssreg,ssresid}.
Если значение stats равно False или опущено, LinEst возвращает только коэффициенты m и константа b.

Дополнительная статистика регрессии выглядит следующим образом.

Статистика регрессии	Описание
se1,se2,...,sen	Стандартные значения ошибок для коэффициентов m1,m2,...,mn.
Seb	Стандартное значение ошибки для константы b (seb = #N/A, если const имеет значение False).
R2	Коэффициент определения. Сравнивает оценочные и фактические значения y и диапазон в значении от 0 до 1. Если значение равно 1, в выборке имеется идеальная корреляция: между предполагаемым значением y и фактическим значением y нет никакой разницы. С другой стороны, если коэффициент определения равен 0, уравнение регрессии не полезен при прогнозировании значения Y.
Сей	Стандартная ошибка для оценки y.
F	Статистика F или наблюдаемое значение F. Используйте статистику F, чтобы определить, возникает ли наблюдаемая связь между зависимыми и независимыми переменными случайно.
Df	Степени свободы. Используйте степени свободы для поиска F-критических значений в статистической таблице. Сравните значения, которые вы найдете в таблице со статистикой F, возвращенной LinEst, чтобы определить уровень достоверности для модели.
ssreg	Сумма квадратов регрессии.
ssresid	Остаточная сумма квадратов.

На следующем рисунке показан порядок возврата дополнительной статистики регрессии.

Можно описать любую прямую линию с наклоном и y-перехватом: Slope (m). Чтобы найти наклон линии, часто написанной как m, возьмите две точки на линии( x1,y1) и (x2,y2); наклон равен (y2 – y1)/(x2 – x1). Y-intercept (b): y-intercept линии, часто записываемой как b, — это значение y в точке пересечения линии по оси Y. Уравнение прямой линии : y = mx + b. После того как вы узнаете значения m и b, вы можете вычислить любую точку в строке, включив значение y или x в это уравнение. Вы также можете использовать функцию TREND.

При наличии только одной независимой переменной x можно получить значения наклона и y-перехвата напрямую с помощью следующих формул:

Уклона: =INDEX(LINEST(known_y's,known_x's),1)
Y-intercept: =INDEX(LINEST(known_y's,known_x's),2)

Точность строки, вычисленной с помощью LinEst, зависит от степени точечной в данных. Чем линейнее данные, тем точнее модель LinEst . LinEst использует метод наименьших квадратов для определения оптимального соответствия данным. При наличии только одной независимой переменной x вычисления для m и b основаны на следующих формулах:

, что x = AVERAGE(известные x) и y = AVERAGE(known_y's).

Функции подгонки линий и кривых LinEst и LogEst могут вычислить наилучшую прямую или экспоненциальную кривую, которая соответствует вашим данным. Однако вы должны решить, какой из двух результатов лучше всего подходит для ваших данных. Можно вычислить TREND(known_y's,known_x's) для прямой линии или GROWTH(known_y's, known_x's) для экспоненциальной кривой. Эти функции без аргумента new_x возвращают массив значений Y, прогнозируемых вдоль этой линии или кривой в фактических точках данных. Затем можно сравнить прогнозируемые значения с фактическими значениями. Вы можете создать диаграмму для визуального сравнения.

При анализе регрессии Microsoft Excel вычисляет для каждой точки квадратную разницу между предполагаемым значением Y для этой точки и его фактическим значением y. Сумма этих квадратных различий называется остаточной суммой квадратов, ssresid. Затем Excel вычисляет общую сумму квадратов( sstotal). Если const = TRUE или опущено, общая сумма квадратов — это сумма квадратных различий между фактическими значениями y и средним значением y-значений. Если const = FALSE, общая сумма квадратов — это сумма квадратов фактических значений y (без вычитания среднего значения y из каждого отдельного значения y). Затем регрессионные суммы квадратов , ssreg, можно найти в ssreg = sstotal - ssresid. Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента определения r2, что является показателем того, насколько хорошо уравнение, полученное в результате регрессии анализа, объясняет связь между переменными; r2 равно ssreg/sstotal.

В некоторых случаях один или несколько столбцов X (предполагается, что Y и X находятся в столбцах) могут не иметь дополнительного прогнозного значения в присутствии других столбцов X. Иными словами, исключение одного или нескольких X-столбцов может привести к прогнозируемым значениям Y с одинаковой точностью. В этом случае эти избыточные столбцы X следует исключить из модели регрессии. Это явление называется коллинарностью , так как любой избыточный столбец X может быть выражен в виде суммы кратных столбцов X. LinEst проверяет наличие коллинарности и удаляет все избыточные X-столбцы из модели регрессии при их идентификации. Удаленные столбцы X можно распознать в выходных данных LinEst как имеющие коэффициенты 0 и 0 se.

Если один или несколько столбцов удаляются как избыточные, df затрагивается, так как df зависит от количества столбцов X, фактически используемых для прогнозирования. Если df изменяется из-за удаления избыточных столбцов X, также затрагиваются значения sey и F.
Коллинеарность должна быть относительно редкой на практике. Однако один из случаев, когда это более вероятно, заключается в том, что некоторые столбцы X содержат только 0 и 1 в качестве индикаторов того, является ли субъект в эксперименте членом определенной группы. Если const = TRUE или опущен, LinEst фактически вставляет дополнительный столбец X всех 1 для моделирования перехвата. Если у вас есть столбец с 1 для каждого субъекта, если мужчина, или 0, если нет, и у вас также есть столбец с 1 для каждого субъекта, если женщина, или 0, если нет, этот столбец является избыточным, так как записи в нем можно получить, вычитая запись в мужском столбце индикатора из записи в дополнительном столбце всех 1, добавленных LinEst.
df вычисляется следующим образом, если из модели не удаляются X-столбцы из-за коллинеарности: если есть k столбцов known_x и const = TRUE или опущен, df = n - k - 1. Если const = FALSE, . df = n - k В обоих случаях каждый столбец X, удаленный из-за коллинеарности, увеличивает значение df на 1.

Формулы, возвращающие массивы, должны вводиться как формулы массива.

При вводе константы массива, например known_x в качестве аргумента, используйте запятые для разделения значений в одной строке, а точки с запятой — для разделения строк. Символы разделителя могут отличаться в зависимости от параметра языкового стандарта в разделе Региональные и языковые параметрыв панель управления.
Обратите внимание, что значения y, прогнозируемые уравнением регрессии, могут быть недопустимыми, если они находятся за пределами диапазона значений y, используемых для определения уравнения.

Базовый алгоритм, используемый в функции LinEst , отличается от базового алгоритма, используемого в функциях Наклон и Перехват . Разница между этими алгоритмами может привести к разным результатам, если данные не определены и коллинеарны. Например, если точки данных аргумента known_y имеют значение 0, а точки данных аргумента known_x — 1:

LinEst возвращает значение 0. Алгоритм LinEst предназначен для возврата разумных результатов для коллинеарных данных, и в этом случае можно найти по крайней мере один ответ.
Наклон и перехват возвращают #DIV/0! Ошибка. Алгоритм наклона и перехвата предназначен для поиска одного и только одного ответа, и в этом случае может быть несколько ответов.

Поддержка и обратная связь

Есть вопросы или отзывы, касающиеся Office VBA или этой статьи? Руководство по другим способам получения поддержки и отправки отзывов см. в статье Поддержка Office VBA и обратная связь.

Поделиться через