Определения оптимального сочетания пересекающихся скидок
В этом статье описывается как определить оптимальное сочетание пересекающихся скидок в Microsoft Dynamics 365 Commerce.
Если скидки пересекаются, необходимо определить сочетание пересекающихся скидок, которое будет давать самую низкую общую суммы проводки или самую большую общую скидку. Когда сумма скидки варьируется в зависимости от цены приобретенных продуктов, как в обычной розничной скидке "купите один, получите один со скидкой X процентов" (BOGO), этот процесс становится предметом комбинаторной задачи оптимизации.
Эта статья относится к Microsoft Dynamics AX 2012 R3 с исправлением KB 3105973 (выпущено 2 ноября 2015 г.) или более поздней версии, а также к выпуску Dynamics 365 Commerce. Чтобы определить комбинацию пересекающихся скидок для своевременного применения был введен метод применения пересекающихся скидок. Мы называем этот новый метод ранжирование по маржинальным значениям. В методе ранжирования по маржинальным значениям значение рассчитывается для каждой пересекающейся скидки с помощью значения скидки на общих продуктов. Пересекающиеся скидки затем применяются в порядке от самого высокого относительного значения до самого маленького относительного значения. Дополнительные сведения об этом новом методе см. в разделе Метод ранжирования по маржинальным значениям далее в этой статье. Ранжирование по маржинальным значениям не используется, когда на суммы скидок для продукта не влияет другой продукт в проводке. Например, этот метод не используется для двух простых скидок или для простой скидки и скидки за количество одного продукта.
Примеры скидок
Можно создать неограниченное число скидок для общего набора продуктов. Однако в связи с отсутствием ограничения могут возникать проблемы с производительностью при попытке расчета скидок, которые должны использоваться в различных продуктах. Следующие примеры иллюстрируют эту проблему с большей степенью детализации. В примере 1 мы запустим два продукта и две пересекающиеся скидки. Затем, в примере 2, мы покажем, как появляется проблема по мере добавления дополнительных продуктов.
Пример 1. Два продукта и две скидки
В этом примере два продукта необходимы для действия каждой скидки, и эти скидки не могут использоваться вместе. Скидки в данном примере являются скидками Лучшая цена. Обе скидки распространяются на оба продукта. Здесь приведены две скидки.

Для любых двух продуктов лучшая из этих двух скидок зависит от цен этих двух продуктов. Когда цены обоих продуктов равны или почти равны, лучше скидка 1. Когда цена одного продукта существенно меньше цены другого продукта, лучше скидка 2. Вот математические правило для оценки этих двух скидок относительно друг друга.
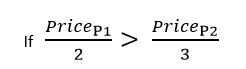
Примечание
Обратите внимание, что когда цена продукта 1 составляет две трети от цены продукта 2, две скидки равны. В этом примере эффективный процент скидки для скидки 1 меняется от нескольких процентов (когда цены на два продукта сильно различаются) до максимального значения 25 процентов (когда два продукта имеют одинаковую цену). Эффективный процент скидки для скидки 2 является фиксированным. Это всегда 20 процентов. Поскольку эффективный процент скидки для скидки 1 имеет диапазон, который может быть больше или меньше, чем скидка 2, лучшая скидка зависит от цен двух продуктов, для которых должна быть предоставлена скидка. В этом примере расчет выполняется быстро, поскольку только две скидки применяются только к двум продуктам. Существует только два возможных варианта: одно применение скидки 1 или одно применение скидки 2. Не требуется рассчитывать никакие перестановки. Значение каждой скидки вычисляется с использованием обоих продуктов, и используется наибольшая скидка.
Пример 2. Четыре продукта и две скидки
Далее мы будет использовать четыре продуктов и эти же две скидки. На все четыре продукта распространяются обе скидки. Существует 12 возможных комбинаций. В итоге две скидки будут применяться к проводке в одной из трех комбинаций: два применения скидки 1, два применения скидки 2 или одно применение скидки 1 и одно применение скидки 2. Чтобы проиллюстрировать возможных комбинаций, рассмотрим два разных набора четырех продуктов, имеющих разные цены:
- Все четыре товара имеют одинаковую цену $15,00. В этом случае наилучшее сочетание скидок — два применения скидки 1. Два продукта по полной цене, и два продукта со скидкой 50 процентов. Итоговая сумма со скидкой для проводки составляет $45 (15 + 15 + 7,50 + 7,50), что на $15 (25 процентов) меньше общей суммы $60 без скидки. Скидка 2 составляет только $12 (20 процентов).
- Два продукта по $20 каждый, один продукт за $15 и один продукт за $5. В этом случае наилучшее сочетание скидок — одно применение скидки 2 и одно применение скидки 1. В следующей таблице показаны эти скидки.
Для использования таблиц следует взять один продукт в строке и один продукт в столбце. Например, в таблице для скидки 1 для сочетания двух продуктов по $20 вы получаете скидку $10. В таблице для скидки 2 для сочетания продукта за $15 и продукта на $5 вы получаете скидку $4.
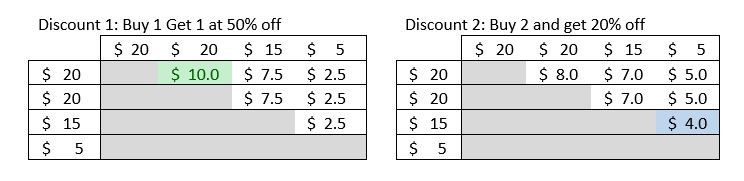
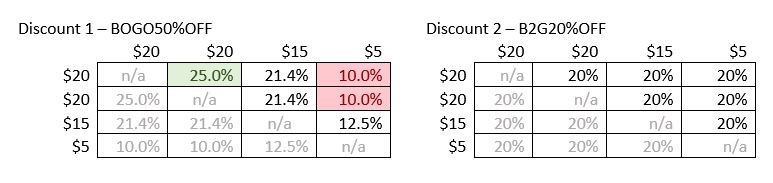
Сначала мы найдем наибольшую скидку, которая доступна для любых двух продуктов с использованием любой из скидок. Эти две таблицы отображает сумму скидки для всех комбинаций двух продуктов. Затененные части таблицы представляют либо случаи, когда продукт сопоставляется сам себе, что не допускается, или обратный порядок связывания двух продуктов, который дает такую же сумму скидки и может быть пропущен. Глядя на таблицы, можно определить, что скидка 1 для двух номенклатур по $20 является наибольшей скидкой, которая доступна для обоих скидок на всех четырех продуктах. (Эта скидка выделена зеленым цветом в первой таблице.) Остаются еще продукт за $15 и продукт за $5. Снова проверив эти две таблицы, можно увидеть, что для этих двух продуктов скидка 1 составляет $2,50, в то время как скидка 2 составляет $4. Поэтому мы выбираем скидку 2. Итоговая скидка составляет $14. Для упрощения визуализации этого обсуждения приведем еще две таблицы, которые показывают процент скидки для всех возможных комбинаций двух продуктов для обоих скидок 1 и 2. Только половина списка комбинаций включена, поскольку для этих двух скидок не имеет значения порядок, в котором два продукта помещаются в скидку. Самая высокая эффективная скидка (25 процентов) выделена зеленым цветом, а самая низкая эффективная скидка (10 процентов) выделена красным цветом.
Примечание
Когда цены различаются и возможно применение двух (или более) взаимоисключающих скидок, единственным способом обеспечения лучшего сочетания скидок является расчет обеих скидок и сравнение их.
Общее число возможных комбинаций
В этом разделе продолжается пример из предыдущего раздела. Мы добавим еще продукты и другие скидки и посмотрим, сколько комбинаций необходимо рассчитать и сравнить. В следующей таблице показано число возможных комбинаций скидок при увеличении количества продуктов. В таблице показано, что происходит при наличии двух пересекающихся скидок, как в предыдущем примере, и при наличии трех пересекающихся скидок. Количество возможных комбинациях скидок, которые необходимо оценить, очень быстро превышает значение, которое даже мощный компьютер может рассчитать и сравнить достаточно быстро, чтобы это было приемлемо для проводок в розничной торговле.
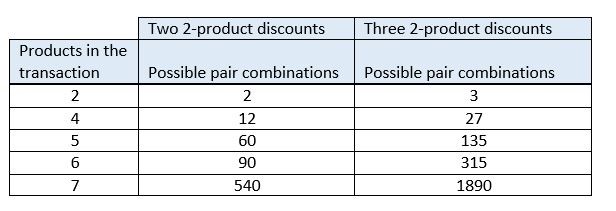
Если продуктов еще большее или применяется еще больше пересекающихся скидок, общее число возможных комбинаций скидок быстро начинает превышать миллионы или даже миллиарды, и время, необходимое для расчета и выбора наилучшего сочетания, быстро становится заметным. Некоторые оптимизации были выполнены в механизме цены, чтобы сократить общее количество комбинаций, которые необходимо оценить. Однако поскольку количество пересекающихся скидок и количества в проводках не ограничены, большое количество сочетаний всегда должно будет вычисляться всякий раз, когда имеются пересекающиеся скидки. Эту проблему решает метод ранжирования по маржинальным значениям.
Метод ранжирования по маржинальным значениям
Для решения проблемы экспоненциального роста числа комбинаций, которые необходимо оценить, существует оптимизация, которая вычисляет значение для каждого общего продукта каждой скидки на наборе продуктов, к которому могут быть применены две и более скидок. Мы называем это значение маржинальным значением скидки для общих продуктов. Маржинальное значение является средним по увеличению продукта в сумме общей скидки, когда общие продукты включены в каждую скидку. Маржинальное значение вычисляется путем определения общей суммы скидки (DTotal), вычитания суммы скидки без общих продуктов (DMinus Shared) и деления этой разницы на количество общих продуктов (ItemsShared).
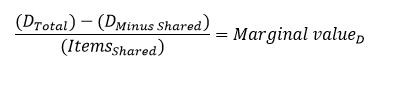
После расчета маржинального значения каждого скидки на общем наборе продуктов скидки применяются к общим продуктом по порядку, строго, от максимального маржинального значения до минимального маржинального значения. В этом методе все остальные варианты скидки не сравниваются каждый раз после применения одного экземпляра скидки. Вместо этого пересекающиеся скидки сравниваются один раз и затем применяются по порядку. Дополнительные сравнения не выполняются. Расчет ранжирования по маржинальным значениям автоматически запускается, когда число общих возможных сочетаний превышает предопределенный порог. Допустимое время расчета общей скидки зависит от отрасли розничной торговли. Однако обычно это время лежит в диапазоне от десятков миллисекунд до одной секунды.