Учебник. Реализация квантового генератора случайных чисел на языке Q#

Статья
01/13/2025

В этом руководстве вы узнаете, как написать базовую квантовую программу, которая Q# использует характер квантовой механики для создания случайного числа.

При работе с этим руководством вы сделаете следующее:

Q# Создайте программу.
Просмотрите основные компоненты Q# программы.
Определите логику проблемы.
Объединение классических и квантовых операций для решения проблемы.
Работа с кубитами и суперпозицией для создания квантового генератора случайных чисел.

Совет

Если вы хотите ускорить путешествие квантовых вычислений, ознакомьтесь с кодом с помощью Azure Quantum, уникальной функцией веб-сайта Azure Quantum. Здесь можно запустить встроенные Q# примеры или Q# собственные программы, создать новый Q# код из запросов, открыть и запустить код в VS Code для Интернета с помощью одного щелчка мыши и задать Copilot любые вопросы о квантовых вычислениях.

Необходимые компоненты

Чтобы запустить пример кода в Copilot в Azure Quantum:
- Учетная запись электронной почты Майкрософт (MSA).
Чтобы разработать и запустить пример кода в Visual Studio Code, выполните следующие действия.
- Последняя версия Visual Studio Code или откройте VS Code в Интернете.
- Последняя версия Quantum Development Kit Azure. Дополнительные сведения об установке см. в разделе Настройка расширения QDK.
- Если вы хотите использовать Jupyter Notebook, необходимо также установить расширения Python и Jupyter , а также последний qsharp пакет Python. Для этого откройте терминал и выполните следующую команду:
```
$ pip install --upgrade  qsharp
```

Определение проблемы

На классических компьютерах действительно случайные числа не создаются, а лишь псевдослучайные. Генератор псевдослучайных чисел создает детерминированную последовательность чисел на основе некоторого начального значения. Для более точной аппроксимации случайных значений этим начальным значением часто является текущее время таймера ЦП.

Квантовые компьютеры, с другой стороны, могут создавать действительно случайные числа. Это связано с тем, что измерение кубита в суперпозиции является вероятностным процессом. Результат измерения является случайным, и нет способа предсказать результат. Это базовый принцип генераторов квантовых случайных чисел.

Кубит — это единица квантовой информации, которая может находиться в суперпозиции. При измерении кубит может принимать только два состояния: 0 или 1. Однако до измерения состояние кубита представляет вероятность получить значение 0 или 1 при измерении.

Для начала возьмите кубит в базовом состоянии, например 0. Первый шаг генератора случайных чисел — использовать операцию Hadamard , чтобы поместить кубита в равное суперпозиции. Измерение этого состояния приводит к нулю или одному с 50% вероятностью каждого результата, действительно случайным битом.

Нет способа знать, что вы будете получать после измерения кубита в суперпозиции, и результатом является другое значение при каждом вызове кода. Но как можно использовать это поведение для создания больших случайных чисел?

Предположим, что вы повторяете этот процесс четыре раза, создав следующую последовательность двоичных цифр:

$${0, 1, 1, 0}$$

Если сцепить (или объединить) эти биты в битовую строку, можно получить большее число. В этом примере битовая последовательность ${0110}$ эквивалентна шести в десятичном формате.

$${0110_{\ binary} \equiv 6_{\ decimal}}$$

Если повторить этот процесс много раз, можно объединить несколько битов для формирования любого большого числа. С помощью этого метода можно создать число для использования в качестве безопасного пароля, так как вы можете убедиться, что хакер не может определить результаты последовательности измерений.

Определение логики генератора случайных чисел

Давайте рассмотрим логику генератора случайных чисел:

Определите max как максимальное число, которое требуется создать.
Определите количество случайных битов, которые требуется создать. Это делается путем вычисления количества битов, nBitsнеобходимо выразить целые числа до max.
Создание случайной битовой строки, длина которой равна nBits.
Если битовая строка представляет число больше max, выполняется возврат к шагу 3.
В противном случае процесс завершается. Возврат созданного числа в виде целого числа.

В качестве примера зададим для max значение 12. То есть 12 — это наибольшее число, которое вы хотите использовать в качестве пароля.

Для представления числа от 0 до 12 требуется ${\lfloor ln(12) / ln(2) + 1 \rfloor}$ или 4 бита. Мы можем использовать встроенную функцию BitSizeI, которая принимает любое целое число и возвращает количество битов, необходимых для представления.

Предположим, что вы создаете битовую строку $${1101_{\ binary}}$, которая эквивалентна ${13_{\ decimal}}$. Так как 13 больше 12, вы повторяете процесс.

Затем создается битовая строка ${0110_{\ binary}}$, которая эквивалентна ${6_{\ decimal}}$. Так как 6 меньше 12, процесс завершен.

Генератор квантовых случайных чисел вернет номер 6 в качестве пароля. На практике в качестве максимального следует задать большее число, поскольку более низкие числа легко взломать простым перебором всех возможных паролей. Чтобы повысить устойчивость пароля к перебору или взлому, можно использовать код ASCII для преобразования двоичных данных в текст и создания пароля с помощью чисел, символов и букв в разных регистрах.

Запись случайного генератора битов

Первым шагом является запись Q# операции, которая создает случайный бит. Эта операция будет одним из стандартных блоков генератора случайных чисел.

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

Теперь давайте изучим этот новый код.

Вы определяете операцию GenerateRandomBit, которая не принимает никаких входных данных и формирует значение типа Result. Тип Result представляет результат измерения и может иметь два возможных значения: Zero или One.
Вы выделяете один кубит с ключевым словом use . При выделении кубит всегда находится в состоянии |0〉.
Операция используется H для размещения кубита в равной суперпозиции.
Операция используется M для измерения кубита, возврата измеренного значения (Zero или One).
Операция используется Reset для сброса кубита в состояние |0〉.

Если мы переводим кубит в состояние суперпозиции с помощью операции H и измеряем его с помощью операции M, при каждом вызове кода возвращаются разные результаты.

Визуализация Q# кода с помощью области Blockh

В сфере Блоха северный полюс соответствует классическому значению 0, а южный — классическому значению 1. Любое состояние суперпозиции обозначается точкой на этой сфере (или стрелкой на схеме). Чем ближе конец этой стрелки к одному из полюсов, тем выше вероятность схлопывания этого кубита при измерении в то классическое состояние, которое соответствует этому полюсу. В примере ниже красная стрелка обозначает состояние кубита с более высокой вероятностью получить значение 0 при измерении кубита.

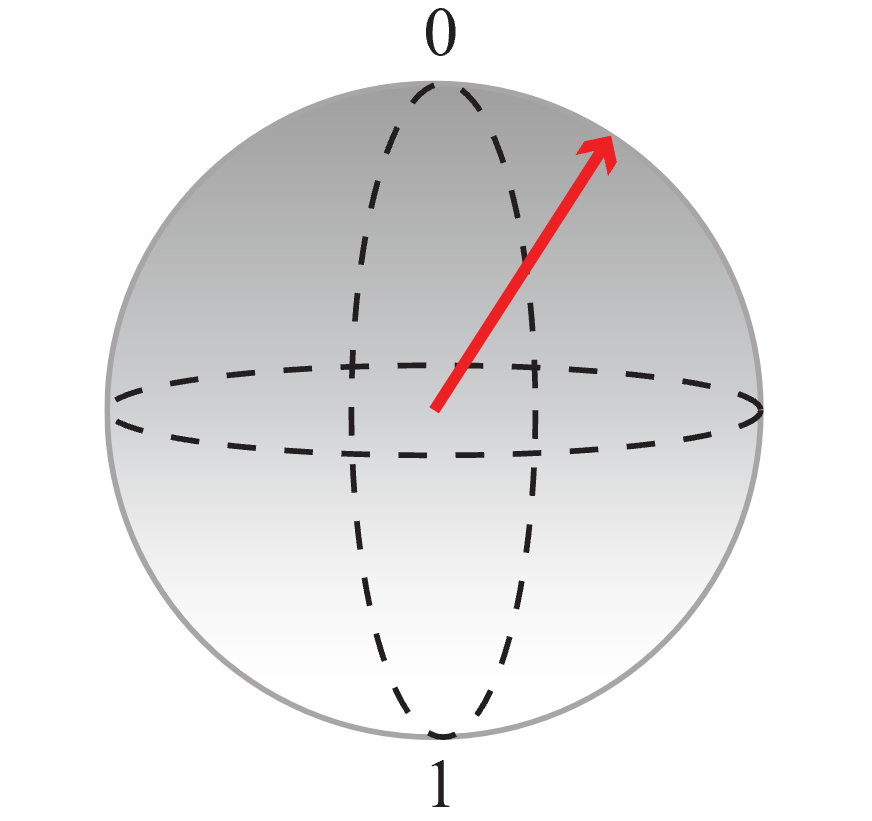
Схема, показывающая состояние кубита с высокой вероятностью измерения нуля.

Вы можете использовать это представление для визуализации работы нашего кода.

Сначала начните с кубита, инициализированного в состоянии |0〉 и примените H операцию для создания равной суперпозиции, в которой вероятности для 0 и 1 совпадают.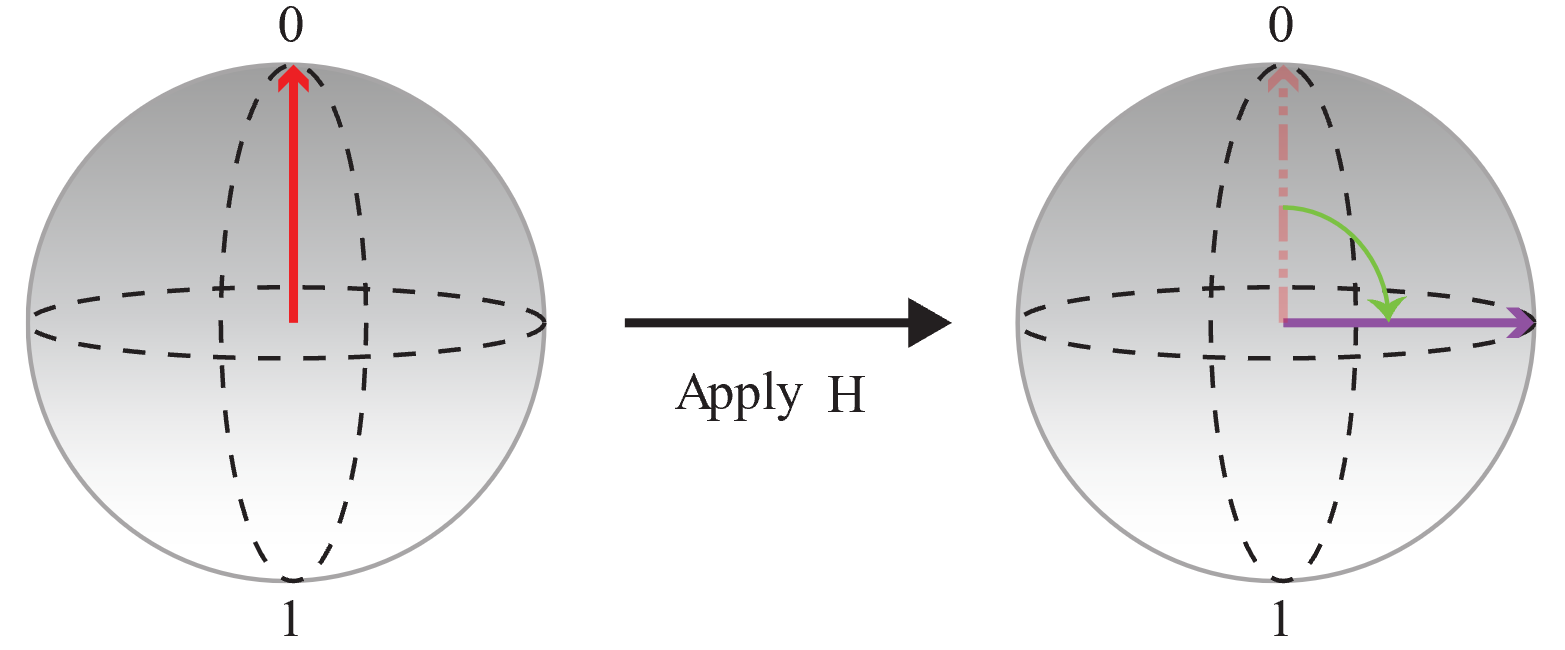
Затем измерьте состояние кубита и сохраните выходное значение:

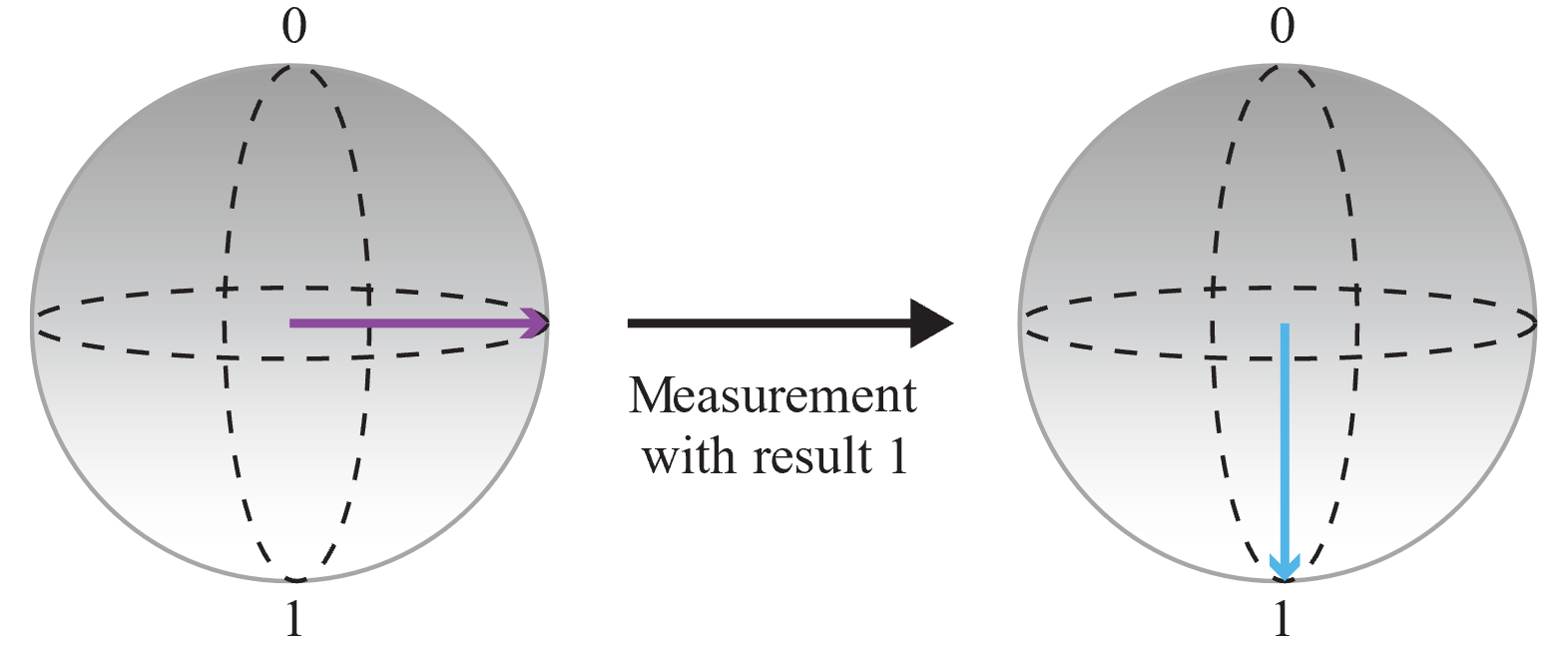
Поскольку результат измерения является случайным и вероятности получения 0 и 1 одинаковы, вы получили совершенно случайный бит. Вызывая эту операцию несколько раз, вы можете создавать большие целые числа. Например, три вызова этой операции предоставят вам три случайных бита, из которых можно собрать трехбитовое число (то есть случайное число в диапазоне от 0 до 7).

Создание полного генератора случайных чисел

Сначала необходимо импортировать необходимые пространства имен из стандартной Q# библиотеки в программу. Компилятор Q# загружает множество распространенных функций и операций автоматически, однако для полного генератора случайных чисел требуются некоторые дополнительные функции и операции из двух Q# пространств имен: Microsoft.Quantum.Mathи Microsoft.Quantum.Convert.
```
import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;
```
Затем определите GenerateRandomNumberInRange операцию. Эта операция многократно вызывает операцию GenerateRandomBit для создания строки битов.
```
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}
```
Рассмотрим этот новый код.
- Необходимо вычислить количество битов, необходимых для выражения целых чисел до max. Функция BitSizeI из Microsoft.Quantum.Math пространства имен преобразует целое число в число битов, необходимых для представления.
- Операция SampleRandomNumberInRange использует цикл for для создания случайных чисел до тех пор, пока не будет получено значение, которое меньше или равно max. Цикл for работает точно так же, как for цикл на других языках программирования.
- Переменная — это изменяемая переменная bits . Изменяемая переменная может изменяться во время вычисления. Для изменения значения изменяемой переменной используется директива set.
- Функция ResultArrayAsInt из пространства имен по умолчанию Microsoft.Quantum.Convert преобразует битовую строку в положительное целое число.
Наконец, вы добавите точку входа в программу. По умолчанию Q# компилятор ищет Main операцию и начинает обработку там. Она вызывает GenerateRandomNumberInRange операцию для создания случайного числа от 0 до 100.
```
operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}
```
Директива let объявляет переменные, которые не меняются во время вычисления. Здесь вы определяете максимальное значение как 100.

Дополнительные сведения об Main операции см. в разделе "Точки входа".
Полный код для генератора случайных чисел выглядит следующим образом:

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using a Hadamard operation
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

Запуск программы генератора случайных чисел

Вы можете запустить программу в Copilot в Azure Quantum и в Visual Studio Code в качестве автономного Q# приложения или с помощью хост-программы Python.

Вы можете протестировать Q# код с помощью Copilot в Azure Quantum бесплатно. Все, что вам нужно, это учетная запись электронной почты Майкрософт (MSA). Дополнительные сведения о Copilot в Azure Quantum см. в статье "Обзор Azure Quantum".

Откройте Copilot в Azure Quantum в браузере.

Скопируйте и вставьте следующий код в редактор кода.

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

Выберите количество выстрелов для выполнения и нажмите кнопку "Выполнить".
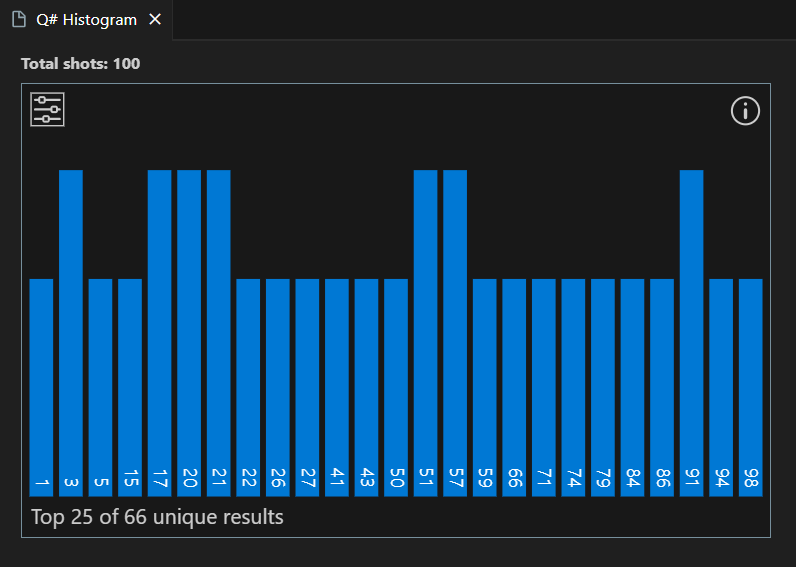
Результаты отображаются в гистограмме и в полях результатов .
Выберите "Объяснить код", чтобы предложить Copilot объяснить вам код.

Совет

В Copilot в Azure Quantum вы можете открыть программу в VS Code для Интернета , нажав кнопку с логотипом VS Code в правом углу редактора кода.

Откройте Visual Studio Code и выберите "Создать > текстовый файл ", чтобы создать новый файл.
Сохраните файл как RandomNumberGenerator.qs. Этот файл будет содержать Q# код для программы.

Скопируйте следующий код в RandomNumberGenerator.qs файле.


import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

Перед запуском target программы необходимо задать для профиля значение "Неограниченный". Выберите представление —> палитра команд, найдите QIR, выберите target QIR Azure Quantum, а затем выберите Q#: неограниченный.
Чтобы запустить программу, выберите Q#" в раскрывающемся списке значка воспроизведения в правом верхнем углу, выберите "Выполнить" из списка команд выше Main()или нажмите клавиши CTRL+F5. Программа выполняет Main() операцию на симуляторе по умолчанию.
Выходные данные будут отображаться в консоли отладки.
Запустите программу еще раз, чтобы увидеть другой результат.

Примечание.

target Если для профиля не задано значение "Неограниченный", при запуске программы появится ошибка.

График гистограммы частоты

Давайте визуализируем распределение результатов, полученных при выполнении квантовой программы несколько раз. Гистограмма частоты помогает визуализировать распределение вероятностей этих результатов.

Выберите представление —> палитра команд и введите гистограмму, которая открывает Q#файл : Запуск файла и отображение параметра гистограммы . Вы также можете выбрать гистограмму из списка команд, описанных выше Main(). Выберите этот параметр, чтобы открыть Q# окно гистограммы.
Введите несколько снимков для выполнения программы, например 100 выстрелов , и нажмите клавишу ВВОД. Гистограмма будет отображаться в Q# окне гистограммы.
Каждая полоса в гистограмме соответствует возможному результату, и его высота представляет количество наблюдаемых результатов. Количество различных результатов может отличаться при каждом запуске гистограммы.

Совет

Вы можете увеличить гистограмму с помощью колесика прокрутки мыши или жеста трекпада. При увеличении масштаба диаграмму можно сдвигать, нажав клавиши ALT при прокрутке.
Выберите панель, чтобы отобразить процент этого результата.
Щелкните значок параметров вверху слева, чтобы отобразить параметры. Вы можете отобразить первые 10 результатов, 25 лучших результатов или все результаты. Вы также можете отсортировать результаты от высокого до низкого или низкого.

В VS Code выберите > команд view и нажмите кнопку Create: New Jupyter Notebook.
В первой ячейке импортируйте qsharp пакет в код Python:
```
import qsharp
```

Q# Добавьте код для программы генератора квантовых случайных чисел. Для этого используйте магическую %%qsharp команду. Обратите внимание, что %%qsharp команда изменяет ячейку записной книжки с типа на тип PythonQ#. Скопируйте этот код во вторую ячейку.

%%qsharp

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

Наконец, запустите код. Вы можете выполнять одно и то же моделирование несколько раз независимо. Каждое независимое моделирование называется "выстрелом". Например, давайте запустите имитацию, 100 раз.
```
results = qsharp.run("Main()", shots=100)
print(results)
```

Примечание.

Этот фрагмент кода в настоящее время не выполняется на любом доступном оборудовании targetsAzure Quantum, так как вызываемому ResultArrayAsInt объекту требуется QPU с полным профилем вычислений.

Ознакомьтесь с другими учебниками по Q#:

Квантовое запутание показывает, как писать Q# программу, которая управляет кубитами и измеряет кубиты и демонстрирует эффекты суперпозиции и запутанности.
Алгоритм поиска Гровера показывает, как написать Q# программу, использующую алгоритм поиска Гровера.
Quantum Fourier Transforms изучает, как писать программу, которая напрямую Q# обращается к определенным кубитам.
Квантовые Катас — это самоуправляемые учебники и упражнения по программированию, направленные на обучение элементам квантовых вычислений и Q# программирования одновременно.

Поделиться через

Учебник. Реализация квантового генератора случайных чисел на языке Q#

Необходимые компоненты

Определение проблемы

Определение логики генератора случайных чисел

Запись случайного генератора битов

Визуализация Q# кода с помощью области Blockh

Создание полного генератора случайных чисел

Запуск программы генератора случайных чисел

График гистограммы частоты

Обратная связь

Дополнительные ресурсы

Поделиться через

Учебник. Реализация квантового генератора случайных чисел на языке Q#

Необходимые компоненты

Определение проблемы

Определение логики генератора случайных чисел

Запись случайного генератора битов

Визуализация Q# кода с помощью области Blockh

Создание полного генератора случайных чисел

Запуск программы генератора случайных чисел

Связанный контент

Обратная связь

Дополнительные ресурсы