Mетоды статистических испытаний (SQL Server 2008) (ru-RU)
SQL Server Технические статьи
Предложенная статья является машинным переводом оригинала.
Обратно тестирование результаты интеллектуального анализа данных с помощью моделирования Монте-Карло
Автор: Buchta Хилмар
Технический рецензент: Cristofor дана
Опубликовано: января 2011 года
Применимо к: SQL Server 2008, SQL Server 2008 R2
Резюме: в этой статье описываются методы статистических испытаний для проверки правильности модели интеллектуального анализа данных. Поэтому предсказанных событий сравниваются с реальных событий в рамках процесса обратно тестирование и пороговое количество ошибок прогноза должен быть определен.
Авторское право
Информация, содержащаяся в настоящем документе представляет текущее представление корпорации Майкрософт по обсуждаемым на дату публикации. Поскольку корпорация Майкрософт должна реагировать на меняющиеся условия рынка, он не должен толковаться как обязательство корпорации Майкрософт, и корпорация Майкрософт не может гарантировать точность представленных сведений после даты публикации.
Этот документ является только в информационных целях. КОРПОРАЦИЯ МАЙКРОСОФТ НЕ ДАЕТ НИКАКИХ ГАРАНТИЙ, ЭКСПРЕСС, ПОДРАЗУМЕВАЕМЫХ ИЛИ УСТАНОВЛЕННЫХ ЗАКОНОМ, В ОТНОШЕНИИ ИНФОРМАЦИИ В НАСТОЯЩЕМ ДОКУМЕНТЕ.
Ответственность за соблюдение всех авторских прав и прав на интеллектуальную собственность целиком и полностью несет пользователь. Без ограничения авторских прав, никакая часть настоящего документа может быть воспроизведены, хранящиеся в, или введена в систему поиска или передана в любой форме или любыми средствами (электронными, механическими, фотокопирование и иным образом), для любых целей без письменного разрешения корпорации Майкрософт.
Корпорация Майкрософт может иметь патенты, патентные заявки, охраняемые товарные знаки, авторские или другие права на интеллектуальную собственность применительно к содержимому этого документа. За исключением, явно указанных в письменном лицензионном соглашении корпорации Майкрософт, предоставление данного документа не дает вам какой-либо лицензии на эти патенты, товарные знаки, авторские права или других видов интеллектуальной свойство.
Если не указано иное, компаний, организаций, продуктов, имена домен , адреса электронной почты, логотипы, люди, места и события являются вымышленными, и никакой связи с реальными компаниями, Организации, продукта, домен имя, адрес электронной почты, логотип, лицо, место или событие предназначен или следует рассматривать как случайное.
© Корпорация Майкрософт, 2011. Все права защищены.
Введение
Интеллектуальный анализ данных часто используется для получения новых знаний от существующих данных. Эти новые знания затем может влиять на будущие бизнес-решений. Обычно эти бизнес-решений содержат какого-либо риска. Например в производственной компании результат процесса интеллектуального анализа данных может быть, что продаж для определенного продукта очень правоподобны для увеличения на следующий период. Логически последовательное решение в данном ��ариант бы увеличение производства для этого изделия для выполнения ожидаемого роста продаж. Если предсказание из процесса добычи оказывается, чтобы быть правдой, все прекрасно. Если нет, полно инвентаризации, но не существует рынка для продукта.
Всякий раз, когда результаты интеллектуального анализа данных используются как основа для бизнес-решений, мы хотим быть уверены в полной мере понять результаты, а также мы хотим иметь возможность доказать, что наши модели интеллектуального анализа данных работают правильно.
Эта статья описывает процесс, который может использоваться для проверки работоспособности модель интеллектуального анализа данных в пределах ожидаемого проверки обратно. Обратно тестирования описанный здесь процесс делает использование Microsoft SQL Server 2008 R2, Microsoft Visual Studio и данных, получаемых с помощью методМонте-Карло. Общие сведения об этих продуктах Майкрософт и Монте-Карло методсодержатся ссылки, расположенные в конце документа.
Обратно тестирование
В стадии разработки, мы можем использовать методы как перекрестные проверки или диаграммы точности интеллектуального анализа данных для понимания статистической значимости модель, как показано в Figure 1 .

Рисунок 1. Инструменты для проверки результатов интеллектуального анализа данных
В противоположность этому обратно тестирования используется для сравнения прогнозов из процесса добычи из прошедший период с реальностью с сегодняшнего дня. К примеру издательская компания хочет, чтобы предсказать, какие клиенты могут отменить их подписки. Для этого они используют интеллектуального анализа данных. Три месяца спустя, они используют задней опробовать подход для проверки прогнозов с реальностью.
Результат обратно тестирования является одним из следующих:
- Модель интеллектуального анализа данных работает как ожидаемые (количество ложных прогнозов в пределах допуска).
- Модель интеллектуального анализа данных не работает, как ожидаемые (количество ложных прогнозы не в пределах допуска).
В последнем вариантобычно пересмотр модели интеллектуального анализа данных является надлежащие действие, чтобы узнать ли не хватает входных переменных или другие важные изменения, которые должны быть отражены в модели интеллектуального анализа данных.
Практический пример, используемый в этой статье
Для того чтобы проиллюстрировать процесс обратно тестирование, этот документ использует данные из фиктивных телекоммуникационной компании. Каждый заказчик имеет 12-месячный контракт, который может быть аннулирована заказчиком на конец периода. Если контракт не расторгнут, он автоматически продолжается еще 12 месяцев. Модель интеллектуального анализа данных в этом примере подготовку для прогнозирования вероятности для аннулирования контракта в течение следующих трех месяцев.
С тем чтобы следовать примеру, мне дали ссылку, перечислены в конце настоящего документа, из которого вы можете скачать образец данных и других ресурсов. Скачать (zip архив) содержит следующее:
- Microsoft SQL Server 2008 R2 резервную копию базы данных (DataMining) с случайным тестовых данных (30 000 дел)
- Решение Microsoft Visual Studio для моделирования Монте-Карло (проект служб Integration ServicesSQL Server ) и визуализация результатов (проектSQL Server служб Reporting Services)
Давайте предположим, что мы сделали прогноз перемешанности 3 месяца назад. Для этой статьи мы не заинтересованы в модели интеллектуального анализа фактических данных, но только в результатах предсказания. Мы хранили результаты базы данных таблица, с именем Mining_Results, как показано в таблице 1.
Table 1. Образец данных (вывод из модели интеллектуального анализа данных)
CaseKey |
Обработка |
ChurnProbability |
1 |
true |
0.874 |
2 |
false |
0.071 |
3 |
false |
0.017 |
4 |
true |
0.502 |
5 |
false |
0.113 |
6 |
false |
0.160 |
7 |
false |
0.069 |
8 |
false |
0.018 |
9 |
false |
0.026 |
10 |
false |
0.187 |
… |
… |
… |
столбец перемешанности содержит прогнозы от алгоритма интеллектуального анализа. Обработка значение true означает, что в данном конкретном вариант, клиент, скорее всего, аннулировать контракт. Уровень обработка (показан в ChurnProbability столбец) содержит выходные данные от добычи функция PredictProbability(Churn,true). Вероятность — это на самом деле отношение отмена всех дел, которые считаются аналогичные алгоритмом интеллектуального анализа данных, с соотношением, представлены в виде числа от 0 (значение 0%) до 1 (значение 100%). К примеру когда мы принимаем взглянуть на первую строку таблицы 1, вероятность является 0.874. Это означает, что 87,4% всех подобных случаев отменили их контракта. На самом деле расчет вероятности является немного более сложным, но в целом, это объяснение обеспечивает хорошее понимание как вычисляется вероятность.
Таблица 1 — это единственный вход, для такого рода анализ обратно тестирование. Это означает, что этот процесс не зависит от выбранной добычи алгоритм (до тех пор, пока алгоритм обеспечивает вероятность прогноза).
Потому что предсказание было выполнено три месяца назад, компания теперь можно сравнить фактические результаты с прогноза. Сколько предсказание ошибки случаются? Модель работает правильно?
Сколько предсказание ошибки можно ожидать?
Если модель интеллектуального анализа данных работает правильно, перемешанности вероятность 0.874 для одного договора означает, что 87,4% аналогичных случаях отменены их контракта. Следовательно это означает, что 100 процентов минус 87,4 процента, или 12,6 процента, подобных случаев не отменена их контракта. Так, всякий раз, когда ал��оритм интеллектуального анализа предсказал вариант как обработка = true, вероятность ошибки является 1-ChurnProbability. В тех случаях, которые, согласно прогнозам, как обработка = false (то есть, где ChurnProbability является менее 50 процентов), вероятность ошибки равен ChurnProbability.
Это значит, мы можем рассчитать количество ожидаемых прогнозирования сбоев с помощью следующих Transact-SQL запрос.
Выберите сумма (дело обработка
КОГДА 1, а затем 1 - churnprobability
ОСТАЛЬНОЕ churnprobability
КОНЕЦ) как errorcount
ОТ [dbo].[Mining_Result]
Для этого примера запро�� приводит к 2126 ожидаемых предсказания ошибок (из в общей сложности 30 000 дел в рамках выборки данных, набор). Это позволяет отличить ложный положительный результат от ложных отрицательных предсказание ошибки, но эта статья расскажет о только всего предсказание ошибки.
Ожидаемое поведение запрос данных бы, что он будет соответствовать прогнозирования качества испытаний данных, набор, и действительно, этот запрос возвращает номер соответствует с выходом матрица классификации при построении матрица классификации, с использованием данных испытаний, набор. Матрица классификации для проверки данных, набор это значение по умолчанию в среде Business Intelligence Development Studio. Она также может быть запрошен путем вызова функция SystemGetClassificationMatrix расширений (Интеллектуального анализа данных) хранятся и второго параметра в значение 2 (1 означает обучающих данных, 2 тестовых данных, 3 обоих), как показано в следующем примере.
Звоните SystemGetClassificationMatrix(Churn_Rate_DT,2,ContractCancelled')
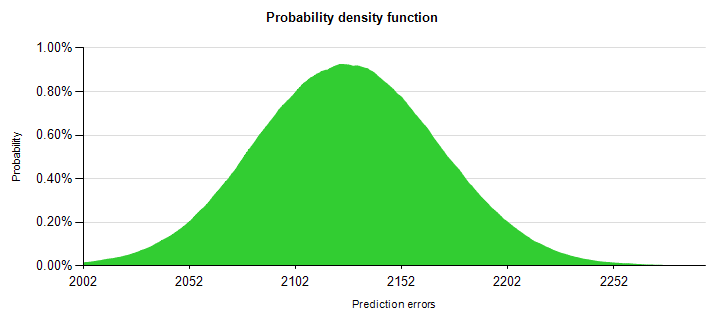
Количество 2126 ожидаемых предсказания ошибок является просто теоретическое число, потому что модель интеллектуального анализа данных является просто аппроксимацию поведение реальных клиентов. В действительности это очень вероятно, что будет существовать различное количество ошибок. ключ к обратно тестирование подход является понимание распределения предсказания ошибок. Дистрибутив можно представить в виде плотности функция. Figure 2 показывает эта функция , основанная на данных примеров набор.
Рисунок 2. функция плотности вероятности для количество ошибок прогноза
Прежде чем мы уйдем на более подробные сведения о том, как производить эту схему, давайте тратить время в результате. Во-первых мы видим пика где-то между 2,102 и 2,152. Это соответствует предыдущий результат запрос 2126 предсказания ошибок. Зеленый район затенены соответствует 100%. Тем не менее вероятность для пикового значения составляет менее 1%. Таким образом вероятность увидеть точно 2126 предсказание ошибки (если модель является правильным) — менее 1 процента.
Монте-Карло моделирование
Для известных распределения функций можно легко изобразить плотности вероятности функция . Например многие из этих функций могут непосредственно использоваться в Microsoft Office Excel, как нормальное распределение, гамма-распределение или распределения хи-квадрат. Однако если распределение ничего не известно, определение плотности вероятности функция является более сложным. Моделирование по методу Монте-Карло часто используются для вычисления функцияплотности вероятности.
В принципе Монте-Карло моделирование для нашего образца предсказание перемешанности работает следующим образом:
- Создайте пустой гистограммы таблица , который сопоставляется число отмененных количество сценариев, в которых завершилось это число отмененных.
- У n петли (сценарии).
Для каждого цикла:- Первоначально набор количество аннулированных контрактов x для этого сценария к нулю.
- Посмотрите на каждом вариант (внутренний цикл):
- Вычислить случайное число r.
- Основываясь на этом случайное число, решать ли вариант считается прогнозирования ошибку путем сравнения r с ChurnProbability.
- Если обнаружена ошибка, увеличить x.
- В конце каждого сценария, увеличить количество вхождений x отмены в Гистограмма таблица.
Например первый сценарий может привести в 2105 предсказание ошибки. Это значит, что Гистограмма таблица выглядит следующим образом:
2105 à 1
В 2,294 отмены завершился второй сценарий. Теперь Гистограмма таблица выглядит следующим образом:
2105 à 1
2294 à 1
Если Третий сценарий заканчивается 2105 отмены снова, гистограмма таблица выглядит следующим образом:
2105 à 2
2294 à 1
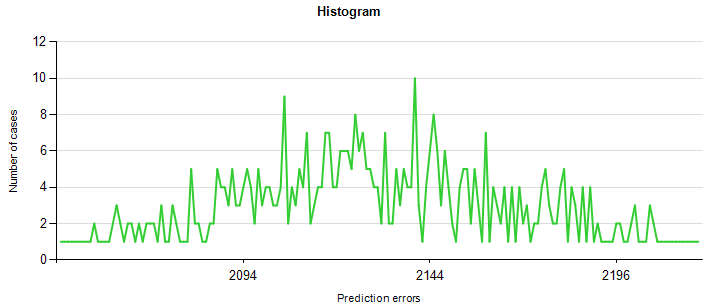
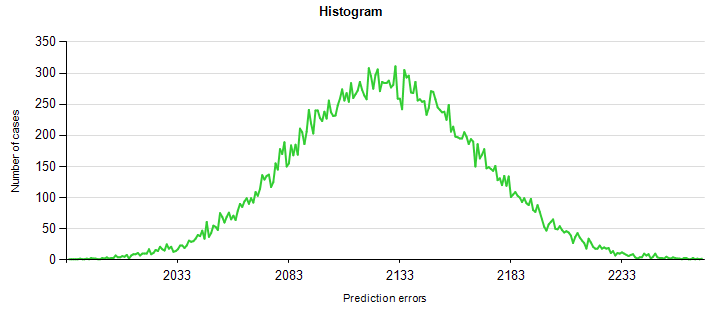
Как правило многие сценарии должны быть вычислено для того чтобы получить относительно плавный график. Ниже приведены некоторые примеры.
50 сценарии |
|
500 сценарии |
|
5000 сценарии |
|
30 000 сценарии |
|
100 000 сценарии |
|
300 000 сценарии |
Как вы можете видеть, диаграмма становится более гладкой другие сценарии используются для моделирования. Однако используются другие сценарии, получает больше времени вычислений. В этом примере для 300 000 сценариев существует 9 миллиардов вычислений в общей сложности (потому что внутренний цикл состоит из 30 000 дел здесь). Таблицу из Figure 2 — сглаженная версия моделирования с 30 000 сценариев.
Используя этот подход позволяет вычислить приближенное к плотности вероятности функция не фактически зная тип распределения.
Моделирование по методу Монте-Карло используются во многих отношениях, например:
- Управление финансовыми рисками (инвестиционный банкинг)
в отличие от нагрузочное тестирование, которая использует четко определенных исторических событий, Монте-Карло моделирование может использоваться для имитации непредсказуемые последствия на рынках. Исходя из плотности функция, меры как значение риску (VaR) может быть вычислено. - Прогноз заказа клиента (CRM)
каждое предложение связано с вероятностью (вероятность). Сколько заказов мы можем ожидать? Например насколько вероятно это что мы видим менее 500 заказов? - Проект управления рисками
том Демарко и Тимоти Листер использовать Монте-Карло симуляции, чтобы получить хорошее понимание последствий (время/стоимость) риски проекта в их книге танцует вальс С медведями (см. ссылку [2] в конце настоящего документа).
функцияплотности вероятности
Переход от гистограммы плотности вероятности функция , как показано в Figure 2 довольно проста. Вы просто должны заменить количество дел по y -ось с вероятностью, который является количество дел, деленная на число сценариев, которые были использованы для моделирования Монте-Карло.
Для обеспечения статистических испытаний, конкретные результаты точно n отмена не является очень интересным. Но основан на функция плотности вероятности это легко для вычисления вероятности для любого диапазон результатов. Например, если вы заинтересованы в том, как скорее всего это видеть между 2100 и 2200 предсказание ошибки, достаточно для расчета площади под графиком в этом диапазон. Для непрерывное распределение это будет интеграл, но потому, что этот пример является дискретного распределения, вы можете просто суммировать значения.
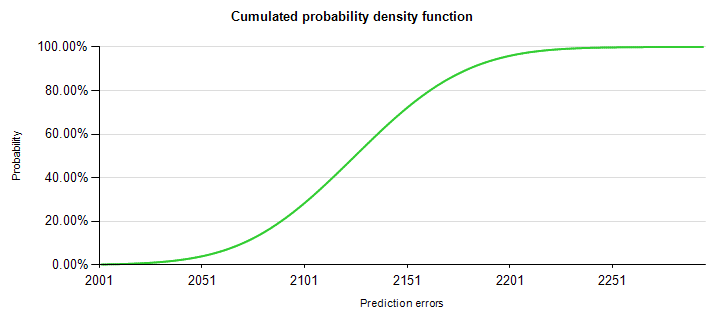
Во многих случаях, вы можете быть заинтересованы в вероятности для видя до n предсказание ошибки (вместо того, точно n предсказание ошибки). Эта вероятность рассчитывается с использованием погашение аккумулированной вероятности функция (сумма в диапазон от 0 до n) как показано в Figure 3 .
Рисунок 3. функция погашение аккумулированной плотности данных изFigure 2
Например весьма маловероятно (почти 0 процентов) чтобы менее 2000 отмены, но это весьма вероятно (почти 100 процентов) видеть меньше 2251 отмены.
Перед созданием статистический тест, Монте-Карло моделирования должны быть на месте. Следующем разделе объясняется, как выполнять Монте-Карло моделирование с использованием SQL Server Integration Services.
Реализация Монте-Карло моделирование в службах Integration Services
В этом разделе показано, как выполнить Монте-Карло моделирование как компонент сценария служб Integration Services.
Шаг 1: Создайте выходную таблица
Выходная таблица используется для хранения результаты моделирования Монте-Карло. Строго говоря, необходимы только два столбца: столбец NumCases представляет количество ошибок прогноза и столбец Count представляет количество случаев, для которых Монте-Карло симуляции закончился в это определенное количество ошибок прогноза.
Остальные столбцы используются для дополнительных вычислений и будет объяснено ниже в этой статье.
Создание таблицы [dbo].[Mining_Histogram]()
[NumCases] [int] NOT NULL,
[Count] [int] NULL,
[Вероятности] [float] NULL,
[TotalProbability] [float] NULL,
[BetaCount] [int] NULL,
[BetaProbability] [float] NULL,
[BetaTotalProbability] [float] NULL
)
Шаг 2: Создание служб Integration Services пакет
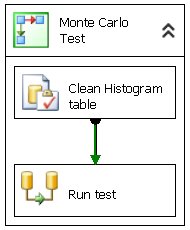
В среде Business Intelligence Development Studio, создайте новый пакет с помощью источник данных (база данных с результатами интеллектуального анализа данных, как показано в Table 1 и вывода таблица , созданной на первом шаге). Добавьте задачу «Выполнение SQL» и задачу «Поток данных» в пакет , как показано в Figure 4 .
Рисунок 4. Поток управления для моделирования Монте-Карло
Задача «Выполнение SQL» используется для удаления всех данных из гистограммы таблица , созданной на шаге 1, так что вы начинаете с пустой гистограммы.
усечение таблица Mining_Histogram
Шаг 3: Добавлениеобласть переменные пакет
Для облегчения конфигурация используются две переменные.
MonteCarloNumCases используется чтобы набор количество сценариев (внешний цикл). BetaValue используется для Модель ошибок, которая обсуждается ниже.
Шаг 4: Реализовать потока данных
Добавьте следующие компоненты потока данных в задаче потока данных.
Рисунок 5. Поток данных для моделирования Монте-Карло
Данных источник просто выбирает все строки из таблицаMining_Result.
ВыберитеCaseKey, сбивать, ChurnProbability
FROM dbo.Mining_Result
Шаг 5: Определение выходных столбцов для тестирования методом Монте-Карло
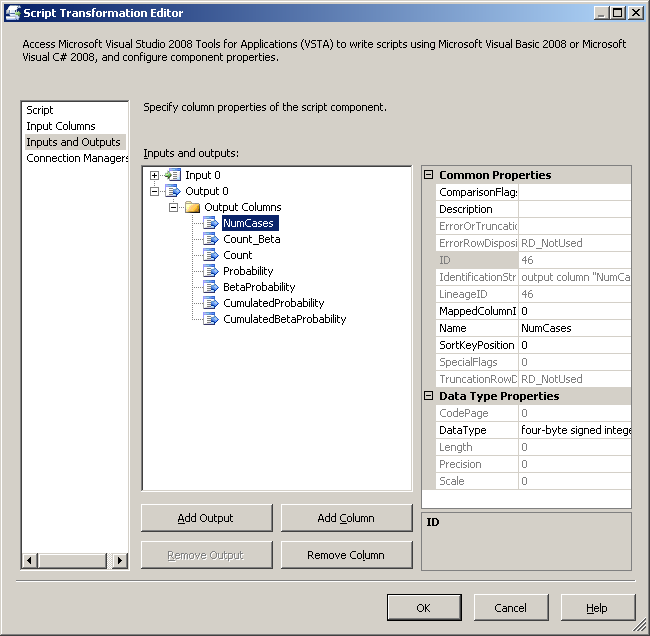
Для компонента сценария добавьте пользовательские переменные, User::BetaValue и User::MonteCarloNumCases, как переменные только для чтения. Затем добавьте следующие столбцы как выходные столбцы.
Рисунок 6. Выходные столбцы для компонента сценария
Колонка |
Тип данных |
Описание |
|---|---|---|
NumCases |
DT_I4 |
Количество случаев |
Count_Beta |
DT_I4 |
Количество сценарии ошибка модель, которая завершилась такое количество случаев |
Граф |
DT_I4 |
Количество сценариев, в которых завершилась такое количество случаев |
Вероятность |
DT_R8 |
Вероятность этого количество случаев (граф поделена общее число сценариев, Монте-Карло) |
BetaProbability |
DT_R8 |
Вероятность этого количество вариантов для модели ошибка |
CumulatedProbability |
DT_R8 |
Погашение аккумулированной вероятность |
CumulatedBetaProbability |
DT_R8 |
Погашение аккумулированной вероятность модель ошибок |
Шаг 6: Напишите сценарий для моделирования Монте-Карло
Введите следующие строки в сценарий для компонента сценария, написанная на C#. Код содержит некоторые основные лесозаготовок, а также вычисляет дополнительные поля для вывода таблица.
с помощью системы;
с помощью System.Data;
с помощью Microsoft.SqlServer.Dts.Pipeline.Wrapper;
с помощью Microsoft.SqlServer.Dts.Runtime.Wrapper;
с помощью System.Collections;
с помощью System.Windows.Forms;
Microsoft.SqlServer.Dts.Pipeline.SSISScriptComponentEntryPointAttribute
государственные класса ScriptMain : UserComponent
{
ArrayList дел;
int numloops = 0;
двойной betavalue;
Строка компонент = «Монте-Карло симулятор»;
Hashtable ht =null;
Hashtable ht_beta = null;
государственные переопределить void PreExecute()
{
базовый.PreExecute();
случаях = новый ArrayList();
numloops = Variables.MonteCarloNumCases;
betavalue = Variables.BetaValue;
HT = новый Hashtable(numloops / 50);
ht_beta = новый Hashtable(numloops / 50);
}
государственные переопределить void PostExecute()
{
базовый.PostExecute();
}
государственные переопределить void Input0_ProcessInputRow (Input0Buffer строку)
{
if (!Случаи Row.ChurnProbability_IsNull).Add(Row.ChurnProbability);
}
государственные переопределить void Input0_ProcessInput (Input0Buffer буфера)
{
bool манекен = действительно;
в то время как (Buffer.NextRow())
{
Input0_ProcessInputRow(buffer);
}
ComponentMetaData.FireInformation (0, компонент, "случаев загрузки:" + случаев.Count.ToString(), "", 0, ref манекена);
if (!Buffer.EndOfRowset()) вернуть;
Случайные случайных = новый случайных(12345);
int противодействия;
int counter_beta;
int maxkey = 0;
int minkey = Int32.MaxValue;
для (int lp = 1; LP < = numloops; LP ++)
{
Если (lp % 500 == 0)
ComponentMetaData.FireInformation (0, компонент, "имитируя вариант:" + lp.ToString(), "", 0, ref манекена);
Счетчик = 0;
counter_beta = 0;
foreach (двойной проблемы в случаев)
{
двойной rnd = случайные.NextDouble();
Если ((prob > = 0.5 & & Rnd > prob) || (prob < 0.5 & & Rnd < prob)) счетчик ++;
Если ((prob > = 0.5 & & Rnd > prob-betavalue) || (prob < 0.5 & & Rnd < prob+betavalue)) counter_beta ++;
}
Если (ХТ.ContainsKey(counter))
{
HT [счетчик] = (int) ht [счетчик] + 1;
}
либо
ХТ.Добавить (счетчик, 1);
Если (ht_beta.ContainsKey(counter_beta))
{
ht_beta [counter_beta] = (int) ht_beta [counter_beta] + 1;
}
либо
ht_beta.Добавление (counter_beta, 1);
Если (счетчик > maxkey) maxkey = счетчик;
Если (счетчик < minkey) minkey = счетчик;
Если (counter_beta > maxkey) maxkey = counter_beta;
Если (counter_beta < minkey) minkey = counter_beta;
}
случаи.Clear();
ComponentMetaData.FireInformation (0, компонент, "моделирование сделано. Имитация случаях: " + numloops.ToString(), "", 0, ref манекена);
/ / Записи результата для вывода
двойной case_prob;
двойной case_betaprob;
двойной totalprob = 0;
двойной totalbetaprob = 0;
для (int я = minkey-1; я < = maxkey; i ++)
{
Output0Buffer.AddRow();
Output0Buffer.NumCases = я;
Если (! ХТ.ContainsKey(i))
{
Output0Buffer.Count = 0;
case_prob = 0;
}
еще {}
Output0Buffer.Count = (int) ht [i];
case_prob = ((int) (ht[i])) / ((двойной) numloops);
}
Если (! ht_beta.ContainsKey(i))
{
Output0Buffer.CountBeta = 0;
case_betaprob = 0;
}
либо
{
Output0Buffer.CountBeta = (int) ht_beta [i];
case_betaprob = ((int) (ht_beta[i])) / ((двойной) numloops);
}
Output0Buffer.PROBABILITY = case_prob;
Output0Buffer.BetaProbability = case_betaprob;
totalprob += case_prob;
totalbetaprob += case_betaprob;
Output0Buffer.CumulatedProbability = totalprob;
Output0Buffer.CumulatedBetaProbability = totalbetaprob;
}
}
государственные переопределить void CreateNewOutputRows()
{
}
}
Пожалуйста, обратите внимание на то, что мы инициализировать генератор случайных чисел с фиксированной семян здесь для того чтобы наши вывода воспроизводимости.
…
Случайные случайных = новый случайных(12345);
…
В противном случае каждом запуске пакет приведет к слегка отличающиеся результаты.
Шаг 7: Сопоставление вывод сценария выходную таблица
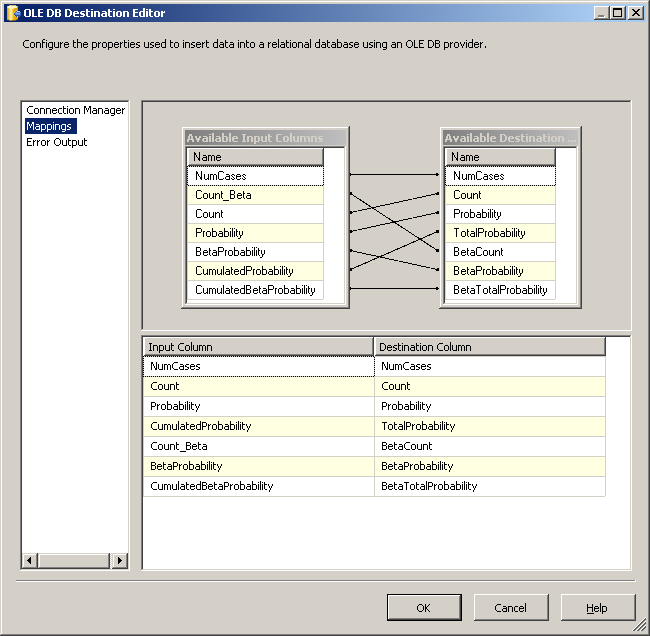
И наконец, вывод сценария необходимо сопоставить с выходную таблица , как показано в Figure 7 .
Рисунок 7. Отображение выходных данных сценария для выходной таблица
Шаг 8: Тестирование пакет
Запустите пакет. Если все правильно, выходной таблица dbo.Mining_Histogram следует устанавливать модули DIMM с 483 строк (для выборки данных из ранее). Первой и последней строк показаны в Figure 8 .
Рисунок 8. Первой и последней строк в Монте-Карло гистограммы таблица
столбец Count хранит количество экземпляров соответствующих сценариев. Например два сценария закончился 1 980 предсказание ошибки, и не сценарий закончилась с 1978 ошибки. столбец TotalProbability содержит простой промежуточных итогов. Таким образом TotalProbability-0 для первой линии и 1 (почти) последней строки. Столбцы с «бета» в имени столбец принадлежат модель ошибок и описаны в следующем разделе.
Проверка статистических гипотез
Проверка статистических гипотез определяет гипотезу и условие теста. До тех пор, как гипотеза проходит условие теста, гипотеза считается правильным.
В этом примере гипотеза, «модель интеллектуального анализа данных работает правильно.» Это условие теста "количество ошибок прогноза является менее н." переменная n параметр тест, который должен определяться.
До тех пор, пока наши обратно тестирование заканчивается менее чем n предсказание ошибки, испытание считается как прошли. В контексте статистики результат теста затем рассматривается «негативный». Однако если есть более чем n ошибки, гипотеза не условие теста и должен быть рассмотрен неправильно. В контексте статистики результат испытания считается «позитивный» в данном вариант.
При выполнении такого рода испытаний, в основном существуют два типа ошибки, мы могли бы сделать:
- По словам испытания модель не так, хотя это правильно.
- По словам испытания модель является правильным, хотя это не так.
Table 2 показывает возможные комбинации между результат теста и реальностью как матрица.
Table 2. Типа I и типа II ошибки
Результат теста |
Модель является правильным (реальность) |
Модель является неправильным (реальность) |
Тест является отрицательным, означает, что модель проходит испытания.
|
Исправить результат (вероятность = 1-альфа. Это значение представляет специфичность испытания.). |
Ошибка типа 2 / бета ошибка. |
Тест является положительным, означает, что эта модель не проходит тест. |
1 Ошибка типа / альфа-ошибки. |
Исправить результат (вероятность = 1-бета. Значение представляет мощности или чувствительность испытания.). |
Если n является очень высоким, риск для ошибку типа 1 низок, и велик риск для ошибку типа 2. С другой стороны если n является низкой, велик риск для ошибку типа 1 и риск для ошибку типа 2 является низким. Искусство тест-дизайн это в выборе приемлемого риска вероятности для тип 1 и тип 2 ошибки. Чтобы сделать это, вам нужно рассчитать ошибок. Это где Монте-Карло результаты полезны.
Чтобы продолжить, нам сначала нужно указать, что действительно подразумевается, когда мы говорим, "модель is incorrect". В принципе нам необходимо определить терпимости. Для того чтобы сделать это, мы используем модель ошибок. Это означает, что оператор «модель is incorrect» преобразуется в «модель альтернативного ошибок является правильным».
источник код, используемый ранее уже включает в себя расчет для этой ошибки модели. В этом примере мы предполагаем, что модель ошибок идет на 0,5% (значение переменной пакет Beta_Value). В источник коде следующие две строки сделать решения для оригинала и альтернативные модели.
...
Если ((prob > = 0.5 & & Rnd > prob) || (prob < 0.5 & & Rnd < prob)) счетчик ++;
Если ((prob > = 0.5 & & Rnd > prob-betavalue) || (prob < 0.5 & & Rnd < prob+betavalue)) counter_beta ++;
...
Figure 9 приведены функции плотности вероятности для двух моделей.
Рисунок 9. функция плотности вероятности для гипотезы и альтернативные модели
Модель ошибок приводит больше ошибок прогноза. Для завершения тестовой конфигурация, мы должны взглянуть на погашение аккумулированной вероятность функции.
Функция |
Описание |
Погашение аккумулированной значение 1 минус вероятность для исходной модели. |
Вероятность для более чем n ошибки, хотя модель исправить. |
Погашение аккумулированной значение вероятности для альтернативного ошибки модели. |
Вероятность для менее чем n ошибки, хотя альтернативная модель исправить (то есть, терпимость является именно 0,5 процента). Это равно с вероятностью того, что именно n возникают ошибки в то время как допуск составляет 0,5 процента или выше. |
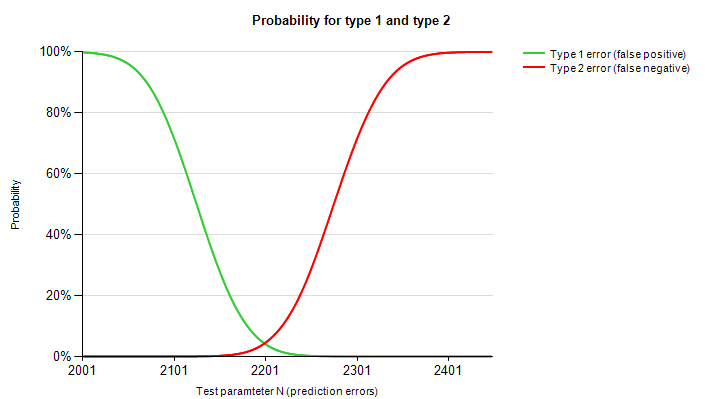
Figure 10 показывает обе функции.
Рисунок 10. Погашение аккумулированной плотности вероятности функция гипотезы и альтернативные модели
Ниже приведены некоторые образцы значений для этих двух видов из-за ошибки, используя таблица показано в Figure 8 и столбцы, NumCases, TotalProbability и BetaTotalProbability.
n (параметра проверки) |
Вероятность возникновения ошибки типа 1 |
Вероятность возникновения ошибки типа 2 |
2,100 |
72.9% |
0.0% |
2,120 |
55.3% |
0.0% |
2,140 |
36.5% |
0.1% |
2,160 |
20.7% |
0.3% |
2,180 |
9.8% |
1.3% |
2,200 |
3.8% |
3.9% |
2,220 |
1.2% |
9.9% |
2,240 |
0.3% |
20.2% |
2,260 |
0.1% |
35.9% |
2,280 |
0.0% |
54.1% |
2,300 |
0.0% |
71.3% |
В этом примере есть низкие значения для тип 1 и тип 2 ошибки на n= 2200. Во многих реальных ситуациях будет невозможно свести к минимуму тип 1 и тип 2 вероятности ошибок в то же время. Это означает, что вам нужно сделать решение ли оптимизировать для низкий тип 1 или типа вероятность 2 ошибки.
Если, к примеру, для испытания призвана держать Ошибка типа 1 ниже 1%, мы могли бы вычислить соответствующие вероятность 2 ошибки типа, с помощью этого запрос.
Выберите TOP 1 numcases AS n,
Круглый(100 * ( betatotalprobability ), 1) AS бета-версии
ОТmining_histogram
WHERE Round(100 * ( 1 - totalprobability ), 1) < 1
ЗАКАЗ BY betatotalprobability
Для этого примера, результирующая вероятность ошибки типа 2 будет около 11,5% с n = 2,224.
С другой стороны мы могли бы также использовать аналогичный запрос типа 1 ошибка вероятности менее 1 процента.
Выберите TOP 1 numcases AS n,
Round(100 * ( 1 - totalprobability ), 1) As Alpha
ОТmining_histogram
ГДЕ
Round(100 * ( betatotalprobability ), 1) < 1
ЗАКАЗ BY betatotalprobabilitydesc
Это приведет к вероятности ошибки типа 1 около 12 процентов и значение 2175 для n.
Резюме и обсуждение
Обратно тестирование может быть бесценным средство для обеспечения того, что ваша организация делает наилучшим образом использовать модели интеллектуального анализа данных прогнозирования. Однако если вы не знакомы с статистические тесты, эта концепция может быть новым. Таким образом в настоящем документе подробно описаны способы выполнения обратно тестирование в гипотетический сценарий, используя SQL Server и Visual Studio. Вот краткое описание теста и его результаты:
- Предпосылкой для этого сценария мы должны модели интеллектуального анализа данных для работы против, наряду с его результаты. Тест сравнивает данные из модели интеллектуального анализа данных для прогнозирования вероятности обработка (нахождение перемешанности баллов для каждого вариант).
- Результаты применения модели используются для маркетинговых целей, поэтому мы хотим быть уверены, что эта модель работает правильно.
- Требования для обратно тестирование должны разработать тест таким образом, чтобы:
- Если модель проходит испытания, компания составляет 99 процентов уверен, что эта модель была действительно правильным.
- запрос используется для определения тестовое условие «количество ошибок прогноза < 2175.»
- Испытания показали, что около 12 процентов вероятности, что модель не может выполнить требования, хотя на самом деле он работает правильно.
Для Модель ошибок мы выбрали простой сдвиг здесь на 0,5 процента. Конечно мы могли бы также выбрали более сложные модели ошибок или даже случайным предположением модель.
Можно также использовать различные моделирование Монте-Карло для других аспектов в процессе интеллектуального анализа данных. Перечислены некоторые примеры, с краткого обсуждения каждого:
Понимание распределения отмены
Монте-Карло моделирование можно использовать для подсчета отмены вместо предсказания ошибок. Например, может потребоваться определить, ответ на этот вопрос: что такое наихудшие количество отмен произойдет (с 95-процентной степенью уверенности)? В статистических терминов это означает, что вы бы вычислить процентили 5 процентов погашение аккумулированной плотности вероятности функция.
Понимание качества матрица классификации
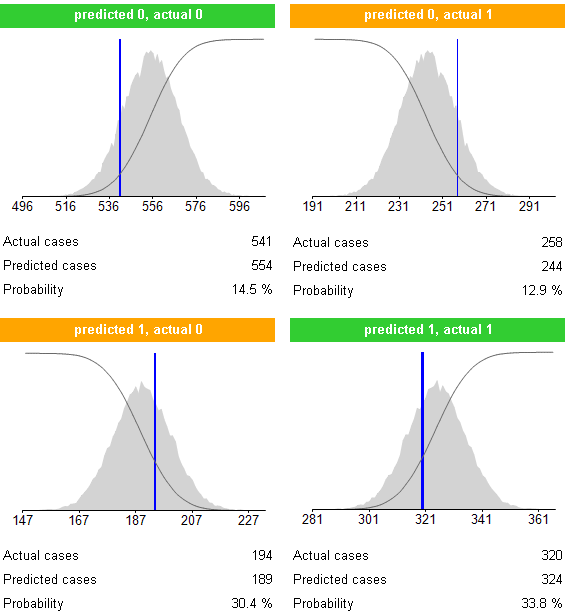
Вы также можете использовать эту имитацию чтобы узнать больше о качество матрица классификации. Как было отмечено ранее количество ошибок прогноза может быть разбита на тип 1 и тип 2 ошибки. Если вы хотите определить качество критерии, используемые для классификации тип ошибки, можно использовать обучающие данные ввода, а не результат интеллектуального анализа данных. Этот метод позволяет сравнить классификацию, основанную на тестовых данных с вероятность ошибки, основанный на обучающих данных. Вывод может быть как показано в Figure 11 . Здесь распределения (затененная область) — плотность, взяты из вероятность ошибки проверки данных. Тонкая линия является погашение аккумулированной плотность (отличаются шкал наось x - и y -ось ) и «голубой линии» является фактическое количество ошибок, основанные на данных испытаний, набор. Чем выше точки, на которой «голубой линии» пересекает погашение аккумулированной плотность, тем лучше это. Например, в Figure 11 , классификации не совсем не соответствует ожиданиям. Обычно в этом вариант, перекрестная проверка свидетельствует о большой стандартное отклонение между разделами тестов.
Рисунок 11. Пример матрица альтернативные классификации
Заключение
Обратно тестирование является хорошей практикой для проверки моделей интеллектуального анализа данных. В обратно тестирование, вы сравнить прежних прогнозов с фактическими результатами для того чтобы доказать, что модель интеллектуального анализа данных все еще работает должным образом. Например рыночные условия могут существенно изменились и модель интеллектуального анализа данных могут не отражать эти изменения; обратно тестирование показывает ли модель интеллектуального анализа данных необходимо скорректировать.
Проверка статистических гипотез строит фон для определения условий теста. Для того чтобы понять вероятности ошибки для теста, распределение прогнозируемого вероятность имеет важное значение. Настоящий документ демонстрирует использование моделирования Монте-Карло для вычисления этого распределения. Для других задач в рамках процесса интеллектуального анализа данных также можно использовать этот тип моделирования.
Для получения дополнительной информации:
http://www.Microsoft.com/SQLServer/: SQL Server веб-сайт
http://TechNet.Microsoft.com/en-US/SQLServer/: SQL Server TechCenter
http://MSDN.Microsoft.com/en-US/SQLServer/: SQL Server DevCenter
http://MS-OLAP.blogspot.com: Buchta Хилмар блог о служб Analysis Services, многомерных Выражений и интеллектуального анализа данных
Ресурсы
[1] Монте-Карло метод – Википедия (http://en.wikipedia.org/wiki/Monte_Carlo_method)
[2] "Танцует вальс С медведями: Управление рисками на проекты программного обеспечения", дом Дорсет, издательская компания, том Демарко и Тимоти Листер '
и
Riskology веб-сайт: http://www.systemsguild.com/riskology/
[3] Плотность вероятности функция - Википедия (http://en.wikipedia.org/wiki/Probability_density_function)
[4] Образцы данных и решение для этой статьи (SQL Server 2008 R2 базы данных резервного копирования и примеры решения) (http://cid-61f98448a5e17d57.office.live.com/self.aspx/%c3%96ffentlich/Validating%20Using%20Monte%20Carlo%20Sim.zip)
Об авторе: Хилмар Buchta — бизнес-аналитики консультант, менеджер проекта и архитектор на ORAYLIS GmbH (http://www.oraylis.de).