クォータニオンの使い方
クォータニオンでボーン処理、その2:クォータニオンの使い方
今回はXNAフレームワーク内でのクォータニオンの使い方の紹介をします。クォータニオンは回転行列の代替として使えるので、Matrix構造体と同じメソッドが用意されています。そこで、同じ操作に対応する行列とクォータニオンの両方のコードを紹介していきます。
回転
回転行列を生成するのと同じようにクォータニオンでもCreateFromYawPitchRoll、CreateFromAxisAngleメソッドを使って任意の回転をするクォータニオンを生成できます。
// 回転行列の生成
Matrix m1 = Matrix.CreateFromYawPitchRoll(yaw, pitch, roll);
Matrix m2 = Matrix.CreateFromAxisAngle(Vector3.Up, angle);
// クォータニオンの生成
// 回転行列とまったく同じ意味のものを生成できる
Quaternion q1 = Quaternion.CreateFromYawPitchRoll(yaw, pitch, roll);
Quaternion q2 = Quaternion.CreateFromAxisAngle(Vector3.Up, angle);
CreateFromYawPitchRollのそれぞれの引数はヨー(Yaw)、ピッチ(Pitch)、ロール(Roll)となっています。飛行機を例にすると、水平飛行状態で機首を左右に回転するのがヨー、機首を上下に回転させるのがピッチ、そして機体の前後を軸とした回転がロールになります。
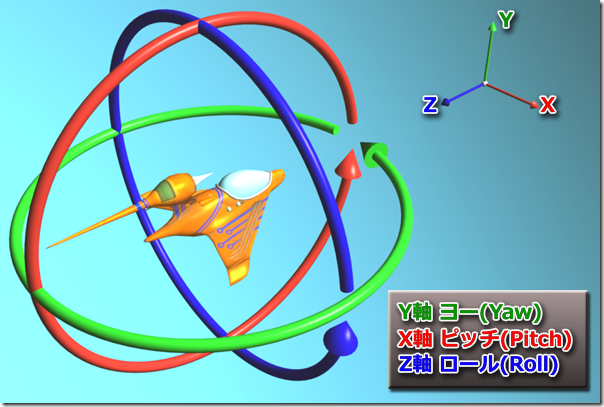
回転していないクォータニオン(単位クォータニオン)
回転していない状態を表すクォータニオンは単位クォータニオンと呼びます。これも行列と同じように、Quaternion.Identityプロパティが使えます。
// 単位回転行列の生成(回転していない行列)
Matrix mi = Matrix.Identity;
// 単位クォータニオン(回転していないクォータニオン)
Quaternion qi = Quaternion.Identity;
結合(Concatenate)
行列と同じように複数のクォータニオンを結合することで、複数の回転を組み合わせたものを生成することができます。q1 * q2のようにして結合ができますが、ここで注意が必要なのは行列の結合の順番とは逆になることです。たとえば、二つの行列をm1 * m2として’結合した場合、意味的には 「m1の回転をした後に、m2の回転をする」 となりますが、クォータニオンの結合、q1 * q2の場合は 「q2の回転をした後に、q1の回転をする」 と違った意味になります。
この原因はXNAフレームワークでは、q1 * q2は結合ではなく、数学的な二つのクォータニオンの乗算として定義されているからです。特に演算子オーバーロードは見た目が数式に近いものが書けるので、数学的な操作と同じように動作するようになっています。これは他の全ての数学関連のクラスや構造体内の演算子オーバーロード(*,/,+,-)でも同じルールに従っています。実はこれがVector3 * Matrixと書けない理由でもあります。
このままだと混乱するので明示的に結合を表すためにConcatenateメソッドがあります。
// 回転行列の結合
// m1の回転をした後に、m2の回転をした結果を計算する
Matrix mtx = m1 * m2;
// クォータニオンの結合
// 順番が行列とは逆になることに注意
// q2 * q1の意味はq1の回転をした後に、q2の回転をするという意味になる
Quaternion quat = q2 * q1;
// 上記の混乱を避けるために明示的にConcatenate(結合)メソッドを呼び出すことで
// q1の回転の後に、q2の回転をした結果を計算できる
quat = Quaternion.Concatenate(q1, q2);
頂点変換
行列を使っての頂点変換は多くの人が使っていると思いますが、クォータニオンを使っても同じように頂点変換ができます。
// 回転行列を使った頂点変換
Vector3 va = Vector3.Transform(position, m1);
// クォータニオンを使った頂点変換
Vector3 vb = Vector3.Transform(position, q1);
クォータニオン、行列間の変換
クォータニオンから回転行列へ、また回転行列からクォータニオンへの変換は以下のメソッドを使ってすることができます。
// クォータニオン、行列間の変換
// クォータニオンから回転行列を生成
Matrix m = Matrix.CreateFromQuaternion(q1);
// 回転行列からクォータニオンを生成する
Quaternion q = Quaternion.CreateFromRotationMatrix(m1);
分解
前述の方法では回転行列とクォータニオン間での変換でしたが、時にはスケールや移動も含まれている行列から回転部分だけを取り出したい場合もあります。この時に便利なのがMatrix.Decomposeメソッドです。
// 任意の行列をスケール、回転(クォータニオン)、移動の三つの情報に分解する
// もともとはコンテントパイプライン内でボーン情報をコンパクトにするために
// 設計されたもので、重い処理なので大量の分解をリアルタイムにするのには向いていない
Matrix boneMatrix = Matrix.Identity;
Vector3 scale;
Quaternion rotation;
Vector3 translation;
boneMatrix.Decompose(out scale, out rotation, out translation);
まとめ
と、いうわけで以上に紹介したようにクォータニオンを回転行列の変わり使えるということが解ったかと思います。注意点としては、結合の順番に気をつけるか、Concatenateメソッドを使うことくらいです。
次回はクォータニオンを使う醍醐味である回転の合成、補間について紹介します。
Comments
Anonymous
April 30, 2009
PingBack from http://microsoft-sharepoint.simplynetdev.com/%e3%82%af%e3%82%a9%e3%83%bc%e3%82%bf%e3%83%8b%e3%82%aa%e3%83%b3%e3%81%ae%e4%bd%bf%e3%81%84%e6%96%b9/Anonymous
February 25, 2014
Matrix world = Matrix.Identity; ためしに挑戦してみました。 以下のクォータニオンを使っていないソースを // 拡大縮小 world *= Matrix.CreateScale(scale * modelfix.scale); // 回転 world *= Matrix.CreateFromYawPitchRoll(draw_rotate.Y , draw_rotate.X , draw_rotate.Z); // 移動 world *= Matrix.CreateTranslation(pos); 以下のソースに変更して無事に同じ動作になりました。 // クォータニオンによる計算 メリット:回転誤差吸収&計算速度はやい? Quaternion world_q = Quaternion.Concatenate( Quaternion.Identity , Quaternion.CreateFromYawPitchRoll(draw_rotate.Y , draw_rotate.X , draw_rotate.Z)); // クォータニオン、行列間の変換 // クォータニオンから回転行列を生成 必ず最後の計算はワールド座標移動 Matrix worldm = Matrix.CreateScale(scale * modelfix.scale) * Matrix.CreateFromQuaternion(world_q); worldm *= Matrix.CreateTranslation(pos); 動作的に問題はありません。 回転しかやっていませんが、こちらの説明の意図を汲んでいる形になっているのでしょうか?Anonymous
February 25, 2014
ペーストが足りなかったです。 world_qの最後の計算の次の行に以下の追加です。 world_q.Normalize();Anonymous
March 23, 2014
返事が遅れてすみませんでした。 提示されたコードでも問題ありませんが、通常、クォータニオンは現在の回転状態を保持するのに使われるので、提示されたコード内のようにdraw_rotateで回転情報を持つ場合はクォータニオンにする必要性は必ずしもありません