Partilhar via

Transformação de projeção (Direct3D 9)

  • Artigo

Você pode pensar na transformação de projeção como controlando os internos da câmera; é análogo à escolha de uma lente para a câmera. Este é o mais complicado dos três tipos de transformação. Essa discussão sobre a transformação de projeção é organizada nos tópicos a seguir.

A matriz de projeção costuma ser uma projeção de perspectiva e escala. A transformação da projeção converte o tronco de exibição em uma forma cuboide. Como a parte perto do final do tronco de exibição é menor do que a extremidade oposta, isso tem o efeito de expandir objetos próximos da câmera; é assim que a perspectiva é aplicada à cena.

No tronco de exibição, a distância entre a câmera e a origem do espaço de transformação da exibição é definido arbitrariamente como D. Portanto, a matriz de projeção se parece com a ilustração a seguir.

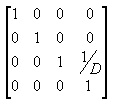
ilustração da matriz de projeção

A matriz de visualização converte a câmera para a origem por meio da translação na direção z por - D. A matriz de translação é como a ilustração a seguir.

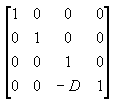
ilustração da matriz de translação

Multiplicar a matriz de tradução pela matriz de projeção (T*P) fornece a matriz de projeção composta, conforme mostrado na ilustração a seguir.

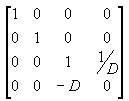
ilustração da matriz de projeção composta

A transformação de perspectiva converte um tronco de exibição em um novo espaço de coordenadas. Observe que o tronco se torna cuboide e também que a origem se move do canto superior direito da cena para o centro, conforme mostrado no diagrama a seguir.

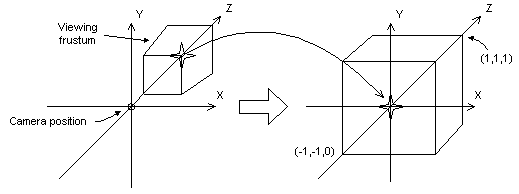
diagrama de como a transformação de perspectiva muda o tronco de exibição em um novo espaço de coordenadas

Na transformação de perspectiva, os limites das direções x e y são -1 e 1. Os limites da direção z são 0 para o plano frontal e 1 para o plano de fundo.

Essa matriz faz a translação e dimensiona objetos com base em uma distância especificada da câmera ao plano de recorte próximo, mas não considera o campo de visão (fov), e os valores de z que produz para objetos na distância podem ser praticamente idênticos, dificultando comparações de profundidade. A tabela a seguir aborda esses problemas e ajusta vértices para levar em conta a taxa de proporção do visor, sendo uma boa opção para a projeção de perspectiva.

ilustração de uma matriz para a projeção de perspectiva

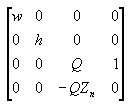
Nessa matriz, Zₙ é o valor de z do plano de recorte próximo. As variáveis w, h e Q têm os significados a seguir. Observe que fovw e fovₖ representam os campos de visão horizontal e vertical do visor em radianos.

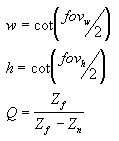
equações dos significados variáveis

Para seu app, usar os ângulos de campo de visão para definir os coeficientes dimensionamento de x e y pode não ser tão conveniente quanto usar as dimensões horizontais e verticais do visor (no espaço da câmera). Após resolução da matemática, as duas equações a seguir para w e h usam dimensões do visor e são equivalentes às equações anteriores.

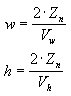
equações dos significados variáveis de w e h

Nessas fórmulas, Zₙ representa a posição do plano de recorte próximo e o Vw e variáveis Vₕ representam a largura e altura do visor no espaço da câmera.

Para um aplicativo C++, essas duas dimensões correspondem diretamente aos membros Width e Height da estrutura D3DVIEWPORT9 .

Seja qual fórmula você decidir usar, lembre-se de definir Zₙ para o maior valor possível, pois os valores de z extremamente próximos da câmera não variam muito. Isso dificulta comparações de profundidade usando buffers de z de 16 bits um pouco complicados.

Assim como acontece com o mundo e as transformações de exibição, você chama o método IDirect3DDevice9::SetTransform para definir a transformação de projeção.

Configurando uma matriz de projeção

A função de exemplo ProjectionMatrix a seguir define os planos de recorte frontal e traseiro, bem como o campo horizontal e vertical dos ângulos de exibição. Os campos de exibição devem ser menores que pi radianos.

D3DXMATRIX 
ProjectionMatrix(const float near_plane, // Distance to near clipping 
                                         // plane
                 const float far_plane,  // Distance to far clipping 
                                         // plane
                 const float fov_horiz,  // Horizontal field of view 
                                         // angle, in radians
                 const float fov_vert)   // Vertical field of view 
                                         // angle, in radians
{
    float    h, w, Q;

    w = (float)1/tan(fov_horiz*0.5);  // 1/tan(x) == cot(x)
    h = (float)1/tan(fov_vert*0.5);   // 1/tan(x) == cot(x)
    Q = far_plane/(far_plane - near_plane);

    D3DXMATRIX ret;
    ZeroMemory(&ret, sizeof(ret));

    ret(0, 0) = w;
    ret(1, 1) = h;
    ret(2, 2) = Q;
    ret(3, 2) = -Q*near_plane;
    ret(2, 3) = 1;
    return ret;
}   // End of ProjectionMatrix

Depois de criar a matriz, defina-a com IDirect3DDevice9::SetTransform especificando D3DTS_PROJECTION.

A biblioteca de utilitários D3DX fornece as seguintes funções para ajudá-lo a configurar sua matriz de projeção.

Uma matriz de projeção amigável para W

O Direct3D pode usar o componente de w de um vértice que foi transformado pelas matrizes de mundo, exibição e projeção para realizar cálculos baseados em profundidade em buffer de profundidade ou efeitos de nevoeiro. Cálculos como esses exigem que sua matriz de projeção normalize w para equivaler ao z do espaço do mundo. Em poucas palavras, se sua matriz de projeção inclui um coeficiente (3,4) que não é 1, todos os coeficientes devem ser dimensionados pelo inverso do coeficiente (3,4) para criar uma matriz adequada. Se você não fornecer uma matriz em conformidade, efeitos de nevoeiro e buffering de profundidade não serão aplicados corretamente.

A ilustração a seguir mostra uma matriz de projeção incompatível e a mesma matriz dimensionada de forma que o nevoeiro relativo aos olhos seja habilitado.

ilustrações de uma matriz de projeção incompatível e uma matriz com nevoeiro relativo aos olhos

Nas matrizes anteriores, todas as variáveis são consideradas diferente de zero. Para obter mais informações sobre neblina relativa aos olhos, consulte Profundidade com base em Olho-Relativo vs. Z. Para obter informações sobre o buffer de profundidade baseado em w, consulte Buffers de profundidade (Direct3D 9).

Direct3D usa matriz de projeção atual definida em seus cálculos de profundidade com base em w. Como resultado, os apps devem definir uma matriz de projeção em conformidade para receber os recursos desejados com base em w, mesmo que eles não usem Direct3D para transformações.

Transformações