Partilhar via

Algoritmo de vetor Quaternion de Orientação do Dispositivo

  • Artigo

Este artigo descreve o algoritmo usado pelo Windows HLK (Kit de Laboratório de Hardware do Windows) para determinar o delta entre o vetor recebido e o esperado para precisão de dados do Eixo 9 nos testes de sensor de orientação avançada. Os testes validam que a fusão do sensor está integrada corretamente e que todos os sensores necessários para a fusão do sensor estão devidamente integrados e instalados.

Observação

Em alguns casos, você pode usar a Ferramenta de Diagnóstico do Sensor para examinar o inclinômetro 3D e o sensor de orientação do dispositivo agregado que está em teste.

Algoritmo de vetor Quaternion

O algoritmo usa o arco cos do produto de ponto 4 dimensional dos dois vetores, dividido pelo produto da magnitude dos dois vetores e dividido por 2. Esse algoritmo é mostrado na Fórmula do Algoritmo de Vetor Quaternion da Figura 1:

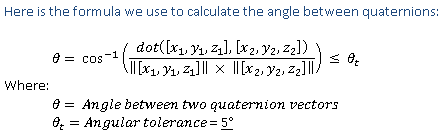
Fórmula do algoritmo de vetor quaternion

Os valores de matriz de rotação são convertidos em valores de quatérnion para validação de precisão. O vetor de quatérnion calculado não deve desviar mais de +/- 5 graus do vetor de quatérnion esperado (tolerância em comparação com o ângulo formado entre vetores de quatérnion) (**+/- precisão de 10 graus permitida na direção do eixo do título). O teste do Windows HLK permite que o delta do Øt seja de até 15 graus.

Como calcular o ângulo delta entre os vetores Quaternion recebidos e esperados

Esta seção descreve o cálculo que calcula o ângulo delta entre os vetores Quaternion recebidos e esperados em Testes de Orientação Avançada no Windows HLK.

Os dois valores de dados a seguir são de interesse no relatório de dados do Sensor de Orientação de Dispositivo Agregado:

  • Vetor quatérnion

  • Matriz de rotação

O teste consiste nas duas verificações a seguir:

  1. Verificação do vetor Quaternion recebido no relatório de dados do sensor. Um vetor Quaternion é da forma (xi + yj + zk + w).

    1. O valor de w é sempre esperado para ser positivo.

    2. Espera-se que o vetor Quaternion seja normalizado e diferente de zero. Por exemplo, a magnitude do vetor deve ser próxima de 1,0. Uma margem de manobra de 1% é fornecida para arredondar erros no cálculo da magnitude.

    3. O ângulo delta é calculado usando delta = 2 * Acos( ( Exp . Rec ) / ( | Exp | * | Rec | ) ) , em que:

      \* indica multiplicação escalar

      . indica produto de ponto

      Exp é o vetor quternion esperado

      Rec é o vetor Quaternion recebido

      | P |indica a magnitude do vetor quternion

      delta é o ângulo em graus

    4. Se delta for maior que 360 graus, o delta será re-calculado como delta = delta - 360.

    5. Neste ponto, o delta deve ser menor ou igual à tolerância a erros; por exemplo, 10 graus.

  2. Verificação da matriz de rotação recebida. Espera-se que a matriz de rotação seja uma matriz 3x3.

    1. Cada vetor de coluna e linha da matriz de rotação deve ser normalizado e diferente de zero. Uma margem de manobra de um por cento (1) é fornecida para arredondar erros no cálculo da magnitude.

    2. A matriz de rotação recebida é transformada em um vetor Quaternion.

    3. Todas as etapas de <um> a <e> de Verificação (1) são reutilizes.

Testar a funcionalidade do sensor com a Ferramenta de Diagnóstico do Sensor

Integrando sensores de movimento e orientação