Regressão Polinomial
Até agora, analisamos apenas modelos de regressão linear; modelos que podem ser modelados como linhas retas. No entanto, os modelos de regressão podem funcionar com praticamente qualquer outro tipo de relacionamento.
O que é regressão polinomial?
A regressão polinomial modela as relações como um tipo particular de curva. Polinômios são uma família de curvas, variando de formas simples a complexas. Quanto mais parâmetros na equação (modelo), mais complexa pode ser a curva.
Por exemplo, um polinômio de dois parâmetros é simplesmente uma linha reta:
y = interceção + B1*x
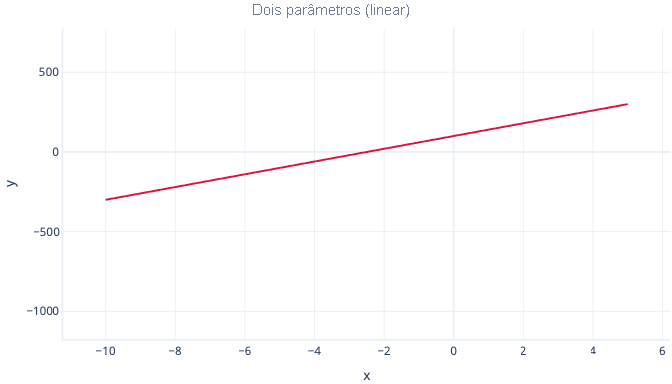
Enquanto um polinômio de três parâmetros tem uma única curva:
y = interceção + B1*x + B2 * x2
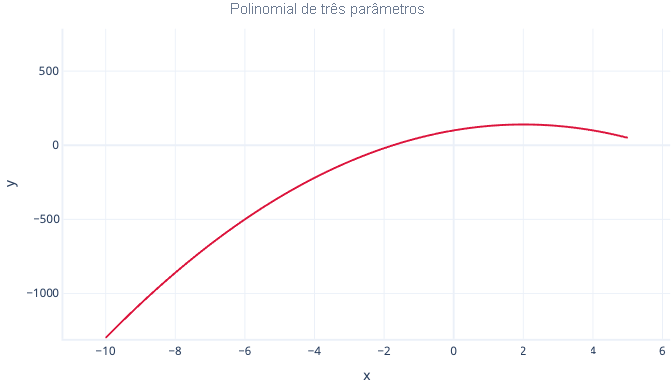
E um polinômio de quatro parâmetros pode ter duas curvas:
y = interceção + B1*x + B2 * x2 + B3 * x3
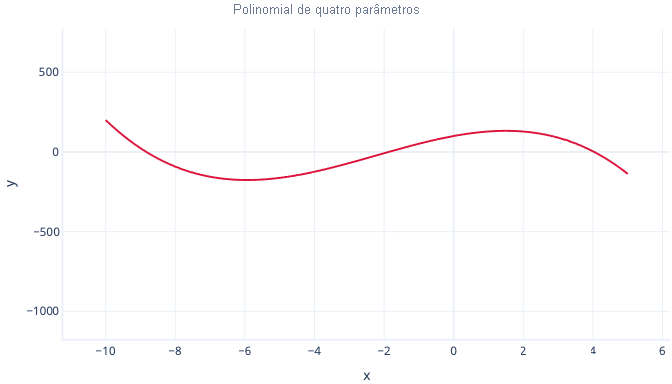
Polinômios versus outras curvas
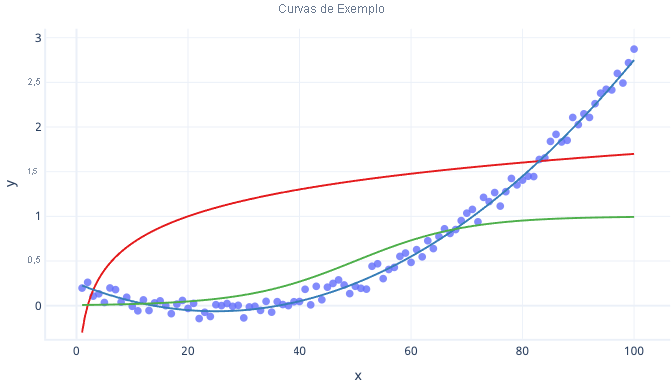
Existem muitos tipos de curvas, como curvas logarítmicas e curvas logísticas (em forma de s), que podem ser usadas com regressão.
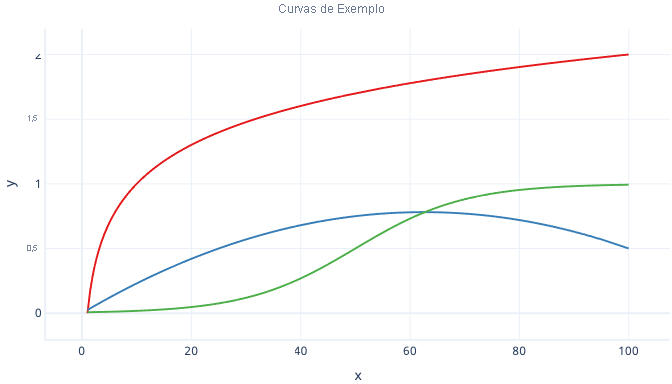
Uma grande vantagem da regressão polinomial é que você pode usá-la para examinar todos os tipos de relações. Por exemplo, você pode usar a regressão polinomial para relações que são negativas dentro de um determinado intervalo de valores de feição, mas positivas dentro de outros. Você também pode usá-lo quando o rótulo (valor y) não tem limite máximo teórico.
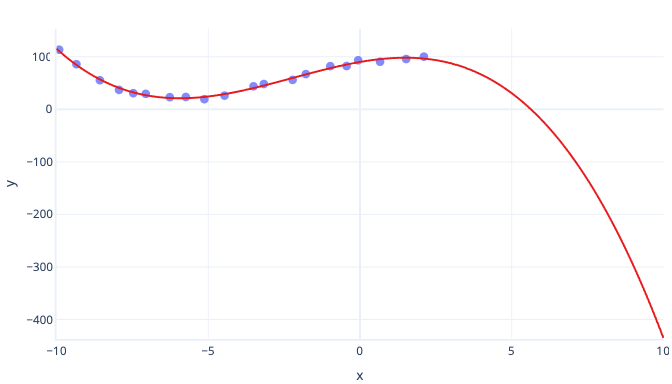
A principal desvantagem das curvas polinomiais é que muitas vezes extrapolam mal. Em outras palavras, se tentarmos prever valores maiores ou menores do que nossos dados de treinamento, os polinômios podem prever valores extremos irrealistas. Outra desvantagem é que as curvas polinomiais são fáceis de superajustar. Isso significa que o ruído nos dados pode alterar a forma da curva muito mais do que modelos mais simples, como a regressão linear simples.
As curvas podem ser usadas com vários recursos?
Vimos como a regressão múltipla pode se ajustar a várias relações lineares ao mesmo tempo. No entanto, não há necessidade de estas se limitarem a relações lineares. Curvas de todos os tipos podem ser usadas para essas relações, quando apropriado. Embora você deva tomar cuidado para não usar curvas como polinômios com vários recursos onde eles não são necessários. Isso ocorre porque as relações podem acabar muito complexas, o que torna mais difícil entender os modelos e avaliar se eles farão previsões que não fazem sentido do ponto de vista do mundo real.