Regressão linear múltipla e R-quadrado

Concluído

Nesta unidade, vamos contrastar a regressão linear múltipla com a regressão linear simples. Também veremos uma métrica chamada R², que é comumente usada para avaliar a qualidade de um modelo de regressão linear.

Regressão linear múltipla

A regressão linear múltipla modela a relação entre várias características e uma única variável. Matematicamente, é o mesmo que a regressão linear simples, e geralmente é ajustado usando a mesma função de custo, mas com mais recursos.

Em vez de modelar uma única relação, esta técnica modela simultaneamente múltiplas relações, que trata como independentes umas das outras. Por exemplo, se estamos prevendo o quão doente um cão fica com base em sua idade e body_fat_percentage, duas relações são encontradas:

• Como a idade aumenta ou diminui a doença
• Como body_fat_percentage aumenta ou diminui a doença

Se trabalharmos apenas com dois recursos, podemos visualizar nosso modelo como um plano — uma superfície 2D plana — assim como podemos modelar a regressão linear simples como uma linha. Vamos explorar isso no próximo exercício.

A regressão linear múltipla tem pressupostos

O fato de que o modelo espera que os recursos sejam independentes é chamado de suposição do modelo. Quando as suposições do modelo não são verdadeiras, o modelo pode fazer previsões enganosas.

Por exemplo, a idade provavelmente prevê o quão doentes os cães se tornam, à medida que os cães mais velhos ficam mais doentes, juntamente com se os cães foram ensinados a jogar frisbee; Cães mais velhos provavelmente todos sabem como jogar frisbee. Se incluíssemos a idade e a knows_frisbee ao nosso modelo como características, isso provavelmente nos diria knows_frisbee é um bom preditor de uma doença e subestimaria a importância da idade. Isso é um pouco absurdo, porque conhecer o frisbee não é suscetível de causar doenças. Por outro lado, dog_breed também pode ser um bom preditor de doença, mas não há razão para acreditar que a idade prediz dog_breed, então seria seguro incluir ambos em um modelo.

Bondade do ajuste: R²

Sabemos que as funções de custo podem ser usadas para avaliar o quão bem um modelo se ajusta aos dados nos quais é treinado. Os modelos de regressão linear têm uma medida especial relacionada chamada R² (R-quadrado). R² é um valor entre 0 e 1 que nos diz quão bem um modelo de regressão linear se ajusta aos dados. Quando as pessoas falam que as correlações são fortes, muitas vezes significam que o valor de R² era grande.

O R² utiliza a matemática para além do que pretendemos abordar neste curso, mas podemos pensá-la intuitivamente. Vamos considerar o exercício anterior, onde analisamos a relação entre idade e core_temperature. Um R² de 1 significaria que os anos poderiam ser usados para prever perfeitamente quem tinha uma temperatura alta e quem tinha uma temperatura baixa. Por outro lado, um 0 significaria que simplesmente não havia relação entre anos e temperatura.

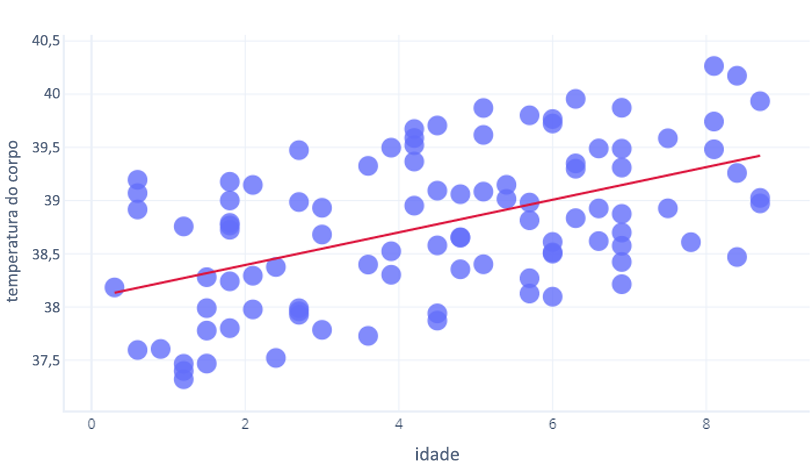
A realidade está algures no meio. Nosso modelo poderia prever a temperatura em algum grau (então é melhor do que R² = 0), mas os pontos variaram um pouco dessa previsão (então é menor do que R² = 1).

R² é apenas metade da história.

Os valores de R² são amplamente aceitos, mas não são uma medida perfeita que podemos usar isoladamente. Sofrem quatro limitações:

• Devido à forma como o R² é calculado, quanto mais amostras tivermos, maior será o R². Isso pode nos levar a pensar que um modelo é melhor do que outro modelo (idêntico), simplesmente porque os valores de R² foram calculados usando diferentes quantidades de dados.
• Os valores de R² não nos dizem quão bem um modelo funcionará com dados novos e inéditos. Os estatísticos superam isso calculando uma medida suplementar, chamada de valor-p, que não abordaremos aqui. No aprendizado de máquina, muitas vezes testamos explicitamente nosso modelo em outro conjunto de dados.
• Os valores de R² não nos dizem o rumo da relação. Por exemplo, um valor de R² de 0,8 não nos diz se a linha está inclinada para cima ou para baixo. Também não nos diz quão inclinada é a linha.

Também vale a pena ter em mente que não há critérios universais para o que torna um valor R² "bom o suficiente". Por exemplo, na maioria da física, é improvável que correlações que não sejam muito próximas de 1 sejam consideradas úteis, mas ao modelar sistemas complexos, valores de R² tão baixos quanto 0,3 podem ser considerados excelentes.