O que é a regressão?

Concluído

A regressão é uma técnica de análise de dados simples, comum e altamente útil, muitas vezes coloquialmente referida como "ajustar uma linha". Em sua forma mais simples, a regressão se ajusta a uma linha reta entre uma variável (característica) e outra (rótulo). Em formas mais complicadas, a regressão pode encontrar relações não lineares entre um único rótulo e vários recursos.

Regressão linear simples

A regressão linear simples modela uma relação linear entre um único recurso e um rótulo geralmente contínuo, permitindo que o recurso preveja o rótulo. Visualmente, pode ser algo como isto:

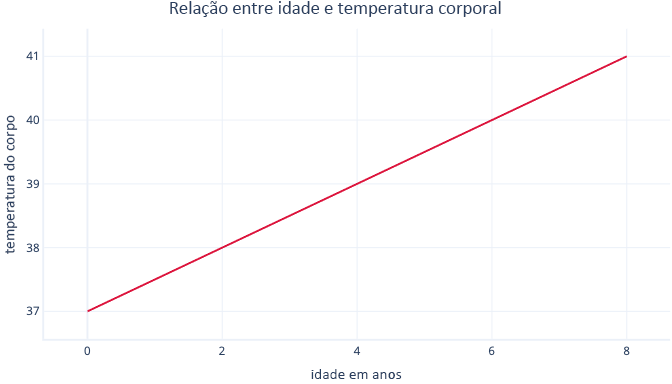
A regressão linear simples tem dois parâmetros: um interceto (c), que indica o valor que o rótulo é quando o recurso é definido como zero, e uma inclinação (m), que indica quanto o rótulo aumentará para cada aumento de um ponto no recurso.

Se você gosta de pensar matematicamente, isso é simplesmente:

y=mx+c

Onde y é o seu rótulo e x é o seu recurso.

Por exemplo, em nosso cenário, se tentássemos prever quais pacientes terão uma temperatura corporal elevada com base em sua idade, teríamos o modelo:

temperatura=m*age+c

E precisa encontrar os valores de m e c durante o procedimento de ajuste. Se encontrássemos m = 0,5 e c = 37, poderíamos visualizá-lo assim:

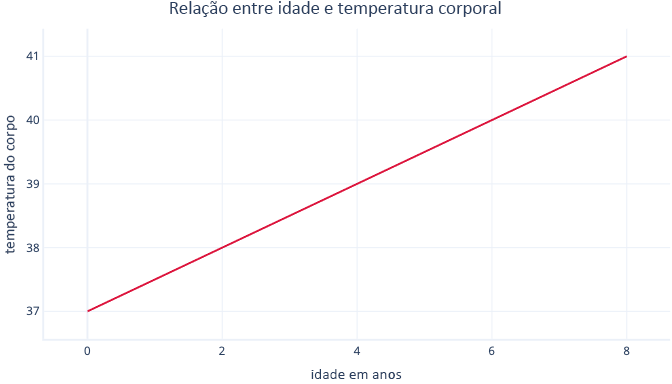
Isto significa que cada ano de idade está associado a um aumento da temperatura corporal de 0,5°C, com um ponto de partida de 37°C.

Ajuste da regressão linear

Normalmente, usamos bibliotecas existentes para ajustar modelos de regressão para nós. A regressão normalmente visa encontrar a linha que produz a menor quantidade de erro, onde erro aqui significa a diferença entre o valor real do ponto de dados e o valor previsto. Por exemplo, na imagem a seguir, a linha preta indica o erro entre a previsão, a linha vermelha e um valor real: o ponto.

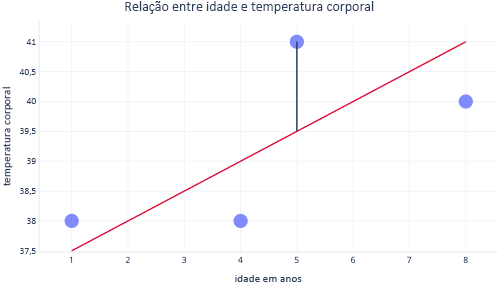
Olhando para estes dois pontos num eixo y, podemos ver que a previsão era de 39,5, mas o valor real era de 41.

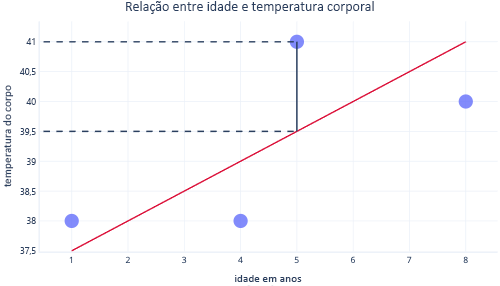
Assim, o modelo estava errado em 1,5 para este ponto de dados.

Mais comumente, ajustamos um modelo minimizando a soma residual de quadrados. Isto significa que a função de custo é calculada assim:

1. Calcule a diferença entre os valores reais e previstos (como anteriormente) para cada ponto de dados.
2. Quadrado esses valores.
3. Soma (ou média) destes valores quadrados.

Esta etapa de quadratura significa que nem todos os pontos contribuem uniformemente para a linha: os outliers – que são pontos que não se enquadram no padrão esperado – têm erros desproporcionalmente maiores, o que pode influenciar a posição da linha.

Pontos fortes da regressão

As técnicas de regressão têm muitos pontos fortes que os modelos mais complexos não têm.

Previsível e fácil de interpretar

As regressões são fáceis de interpretar porque descrevem equações matemáticas simples, que muitas vezes podemos representar. Modelos mais complexos são muitas vezes referidos como soluções de caixa preta, porque é difícil entender como eles fazem previsões ou como eles se comportarão com certas entradas.

Fácil de extrapolar

As regressões facilitam a extrapolação; para fazer previsões para valores fora do intervalo do nosso conjunto de dados. Por exemplo, é simples estimar no nosso exemplo anterior que um cão de nove anos terá uma temperatura de 40,5°C. Deve-se sempre ter cuidado com a extrapolação: este modelo preveria que uma pessoa de 90 anos teria uma temperatura quase quente o suficiente para ferver água.

O ajuste ideal é geralmente garantido

A maioria dos modelos de aprendizado de máquina usa descida de gradiente para ajustar modelos, o que envolve ajustar o algoritmo de descida de gradiente e não fornece nenhuma garantia de que uma solução ideal será encontrada. Por outro lado, a regressão linear que usa a soma dos quadrados como uma função de custo não precisa de um procedimento iterativo de descida de gradiente. Em vez disso, a matemática inteligente pode ser usada para calcular a localização ideal para a linha a ser colocada. A matemática está fora do escopo deste módulo, mas é útil saber que (desde que o tamanho da amostra não seja muito grande) a regressão linear não precisa de atenção especial para ser dada ao processo de ajuste, e a solução ideal é garantida.