O que é a regressão?
A regressão funciona estabelecendo uma relação entre variáveis nos dados que representam características – conhecidas como características – da coisa que está sendo observada e a variável que estamos tentando prever – conhecida como rótulo.
Lembre-se que nossa empresa aluga bicicletas e quer prever o número esperado de aluguéis em um determinado dia. Neste caso, os recursos incluem coisas como o dia da semana, mês e assim por diante, enquanto a etiqueta é o número de aluguéis de bicicletas.
Para treinar o modelo, começamos com uma amostra de dados contendo as características, bem como valores conhecidos para o rótulo; Então, neste caso, precisamos de dados históricos que incluam datas, condições climáticas e o número de aluguéis de bicicletas.
Em seguida, dividiremos este exemplo de dados em dois subconjuntos:
- Um conjunto de dados de treinamento ao qual aplicaremos um algoritmo que determina uma função que encapsula a relação entre os valores de recurso e os valores de rótulo conhecidos.
- Um conjunto de dados de validação ou teste que podemos usar para avaliar o modelo usando-o para gerar previsões para o rótulo e comparando-os com os valores reais conhecidos do rótulo.
O uso de dados históricos com valores de rótulo conhecidos para treinar um modelo torna a regressão um exemplo de aprendizado de máquina supervisionado .
Um exemplo simples
Vamos dar um exemplo simples para ver como funciona o processo de formação e avaliação em princípio. Suponhamos que simplificamos o cenário para que usemos um único recurso – a temperatura média diária – para prever a etiqueta de aluguel de bicicletas.
Começamos com alguns dados que incluem valores conhecidos para o recurso de temperatura média diária e a etiqueta de aluguel de bicicletas.
| Temperatura | Alugueres |
|---|---|
| 56 | 115 |
| 61 | 126 |
| 67 | 137 |
| 72 | 140 |
| 76 | 152 |
| 82 | 156 |
| 54 | 114 |
| 62 | 129 |
Agora vamos selecionar aleatoriamente cinco dessas observações e usá-las para treinar um modelo de regressão. Quando estamos falando em "treinar um modelo", o que queremos dizer é encontrar uma função (uma equação matemática; vamos chamá-la de f) que possa usar o recurso de temperatura (que chamaremos de x) para calcular o número de aluguéis (que chamaremos de y). Em outras palavras, precisamos definir a seguinte função: f(x) = y.
Nosso conjunto de dados de treinamento tem esta aparência:
| x | S |
|---|---|
| 56 | 115 |
| 61 | 126 |
| 67 | 137 |
| 72 | 140 |
| 76 | 152 |
Vamos começar plotando os valores de treinamento para x e y em um gráfico:
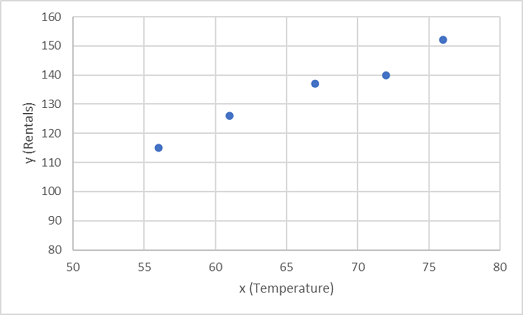
Agora precisamos ajustar esses valores a uma função, permitindo alguma variação aleatória. Você provavelmente pode ver que os pontos plotados formam uma linha diagonal quase reta; Em outras palavras, há uma aparente relação linear entre x e y, então precisamos encontrar uma função linear que seja a melhor opção para a amostra de dados. Existem vários algoritmos que podemos usar para determinar esta função, que finalmente encontrará uma linha reta com variância geral mínima dos pontos plotados; Assim:
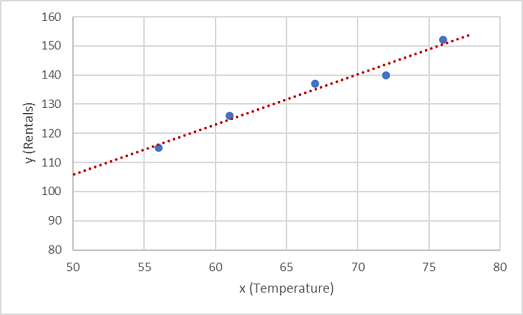
A linha representa uma função linear que pode ser usada com qualquer valor de x para aplicar a inclinação da linha e sua intercetação (onde a linha cruza o eixo y quando x é 0) para calcular y. Neste caso, se estendêssemos a linha para a esquerda, descobriríamos que quando x é 0, y é cerca de 20, e a inclinação da linha é tal que, para cada unidade de x que você se move para a direita, y aumenta em cerca de 1,7. Podemos, portanto, calcular nossa função f como 20 + 1,7x.
Agora que definimos nossa função preditiva, podemos usá-la para prever rótulos para os dados de validação que retivemos e comparar os valores previstos (que normalmente indicamos com o símbolo ŷ, ou "y-hat") com os valores y reais conhecidos.
| x | S | ŷ |
|---|---|---|
| 82 | 156 | 159.4 |
| 54 | 114 | 111.8 |
| 62 | 129 | 125.4 |
Vamos ver como os valores y e ŷ se comparam em um gráfico:
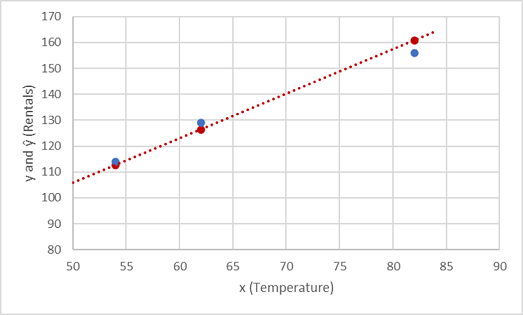
Os pontos plotados que estão na linha da função são os valores ŷ previstos calculados pela função, e os outros pontos plotados são os valores y reais.
Existem várias maneiras de medir a variância entre os valores previstos e reais, e podemos usar essas métricas para avaliar o quão bem o modelo prevê.
Nota
O aprendizado de máquina é baseado em estatística e matemática, e é importante estar ciente de termos específicos que estatísticos e matemáticos (e, portanto, cientistas de dados) usam. Você pode pensar na diferença entre um valor de rótulo previsto e o valor real do rótulo como uma medida de erro. No entanto, na prática, os valores "reais" são baseados em observações amostrais (que podem estar sujeitas a alguma variância aleatória). Para deixar claro que estamos comparando um valor previsto (ŷ) com um valor observado (y), nos referimos à diferença entre eles como os residuais. Podemos resumir os resíduos de todas as previsões de dados de validação para calcular a perda geral no modelo como uma medida de seu desempenho preditivo.
Uma das maneiras mais comuns de medir a perda é quadrar os resíduos individuais, somar os quadrados e calcular a média. A quadratura dos resíduos tem o efeito de basear o cálculo em valores absolutos (ignorando se a diferença é negativa ou positiva) e dar mais peso a diferenças maiores. Essa métrica é chamada de Erro Quadrático Médio.
Para nossos dados de validação, o cálculo tem esta aparência:
| S | ŷ | y - ŷ | (y - ŷ)2 |
|---|---|---|---|
| 156 | 159.4 | -3.4 | 11.56 |
| 114 | 111.8 | 2.2 | 4.84 |
| 129 | 125.4 | 3.6 | 12.96 |
| Soma | ∑ | 29.36 | |
| Média | x̄ | 9.79 |
Portanto, a perda para o nosso modelo baseado na métrica MSE é de 9,79.
Então, isso é bom? É difícil dizer, porque o valor de MPE não é expresso em uma unidade de medida significativa. Sabemos que quanto menor for o valor, menor será a perda no modelo e, portanto, melhor ele está prevendo. Isso torna uma métrica útil para comparar dois modelos e encontrar o que tem melhor desempenho.
Às vezes, é mais útil expressar a perda na mesma unidade de medida que o próprio valor previsto do rótulo; neste caso, o número de alugueres. É possível fazer isso calculando a raiz quadrada do MSE, que produz uma métrica conhecida, sem surpresa, como Root Mean Squared Error (RMSE).
√9,79 = 3,13
Assim, o RMSE do nosso modelo indica que a perda é de pouco mais de 3, o que você pode interpretar vagamente como significando que, em média, previsões incorretas estão erradas em cerca de três aluguéis.
Existem muitas outras métricas que podem ser usadas para medir a perda em uma regressão. Por exemplo, R2 (R-quadrado) (às vezes conhecido como coeficiente de determinação) é a correlação entre x e y ao quadrado. Isso produz um valor entre 0 e 1 que mede a quantidade de variância que pode ser explicada pelo modelo. Geralmente, quanto mais próximo de 1, melhor o modelo prevê.