Avaliar modelos de classificação
A precisão do treinamento de um modelo de classificação é muito menos importante do que o quão bem esse modelo funcionará quando receber dados novos e invisíveis. Afinal, treinamos modelos para que eles possam ser usados em novos dados que encontramos no mundo real. Então, depois de treinarmos um modelo de classificação, avaliaremos como ele se comporta em um conjunto de dados novos e invisíveis.
Nas unidades anteriores, criamos um modelo que preveria se um paciente tinha diabetes ou não com base em seu nível de glicose no sangue. Agora, quando aplicado a alguns dados que não faziam parte do conjunto de treinamento, obtemos as seguintes previsões.
| x | S | ŷ |
|---|---|---|
| 83 | 0 | 0 |
| 119 | 1 | 1 |
| 104 | 1 | 0 |
| 105 | 0 | 1 |
| 86 | 0 | 0 |
| 109 | 1 | 1 |
Lembre-se que x refere-se ao nível de glicose no sangue, y refere-se a se eles são realmente diabéticos, e ŷ refere-se à previsão do modelo sobre se eles são diabéticos ou não.
Apenas calcular quantas previsões estavam corretas às vezes é enganoso ou simplista demais para entendermos os tipos de erros que ele cometerá no mundo real. Para obter informações mais detalhadas, podemos tabular os resultados em uma estrutura chamada matriz de confusão, como esta:
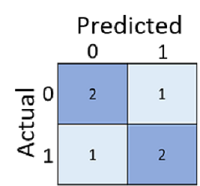
A matriz de confusão mostra o número total de casos em que:
- O modelo previu 0 e o rótulo real é 0 (negativos verdadeiros, canto superior esquerdo)
- O modelo previu 1 e o rótulo real é 1 (verdadeiros positivos, canto inferior direito)
- O modelo previu 0 e o rótulo real é 1 (falsos negativos, canto inferior esquerdo)
- O modelo previu 1 e o rótulo real é 0 (falsos positivos, canto superior direito)
As células de uma matriz de confusão são frequentemente sombreadas para que valores mais altos tenham uma sombra mais profunda. Isso torna mais fácil ver uma forte tendência diagonal de cima-esquerda para baixo-direita, destacando as células onde o valor previsto e o valor real são os mesmos.
A partir desses valores principais, você pode calcular uma série de outras métricas que podem ajudá-lo a avaliar o desempenho do modelo. Por exemplo:
- Precisão: (TP+TN)/(TP+TN+FP+FN) - de todas as previsões, quantas estavam corretas?
- Recall: TP/(TP+FN) - de todos os casos positivos, quantos o modelo identificou?
- Precisão: TP/(TP+FP) - de todos os casos que o modelo previu serem positivos, quantos são realmente positivos?