Analisar a classificação com curvas características do operador recetor

Concluído

Os modelos de classificação devem atribuir uma amostra a uma categoria. Por exemplo, ele deve usar recursos como tamanho, cor e movimento para determinar se um objeto é um caminhante ou uma árvore.

Podemos melhorar os modelos de classificação de muitas maneiras. Por exemplo, podemos garantir que nossos dados sejam equilibrados, limpos e dimensionados. Também podemos alterar nossa arquitetura de modelo e usar hiperparâmetros para extrair o máximo de desempenho possível de nossos dados e arquitetura. Eventualmente, não encontramos melhor maneira de melhorar o desempenho em nosso conjunto de teste (ou hold-out) e declaramos nosso modelo pronto.

O ajuste do modelo até este ponto pode ser complexo, mas podemos usar uma etapa final simples para melhorar ainda mais o funcionamento do nosso modelo. Para entender isso, porém, precisamos voltar ao básico.

Probabilidades e categorias

Muitos modelos têm vários estágios de tomada de decisão, e o último muitas vezes é simplesmente uma etapa de binarização. Durante a binarização, as probabilidades são convertidas em um rótulo rígido. Por exemplo, digamos que o modelo é fornecido com recursos e calcula que há 75% de chance de ter sido mostrado um caminhante e 25% de chance de ter sido mostrado uma árvore. Um objeto não pode ser 75% caminhante e 25% árvore; é um ou outro! Como tal, o modelo aplica um limiar, que é normalmente de 50%. Como a classe de caminhante é maior que 50%, o objeto é declarado como caminhante.

O limiar de 50% é lógico; Isso significa que a etiqueta mais provável de acordo com o modelo é sempre escolhida. No entanto, se o modelo for tendencioso, este limiar de 50% poderá não ser adequado. Por exemplo, se o modelo tem uma ligeira tendência para apanhar árvores mais do que os caminhantes, colhendo árvores 10% mais frequentemente do que deveria, podemos ajustar o nosso limiar de decisão para ter em conta isso.

Atualização sobre matrizes de decisão

As matrizes de decisão são uma ótima maneira de avaliar os tipos de erros que um modelo está cometendo. Isso nos dá as taxas de Verdadeiros Positivos (TP), Verdadeiros Negativos (TN), Falsos Positivos (FP) e Falso Negativos (FN)

Podemos calcular algumas características úteis a partir da matriz de confusão. Duas características populares são:

• Taxa Positiva Verdadeira (sensibilidade): com que frequência os rótulos "Verdadeiros" são corretamente identificados como "Verdadeiros". Por exemplo, com que frequência o modelo prevê "caminhante" quando a amostra mostrada é de fato um caminhante.
• Taxa de falsos positivos (taxa de alarme falso): com que frequência os rótulos "Falsos" são identificados incorretamente como "Verdadeiros". Por exemplo, com que frequência o modelo prevê "caminhante" quando é mostrada uma árvore.

Observar as taxas de verdadeiros positivos e falsos positivos pode nos ajudar a entender o desempenho de um modelo.

Considere o nosso exemplo de caminhante. Idealmente, a taxa de verdadeiros positivos é muito alta, e a taxa de falsos positivos é muito baixa, porque isso significa que o modelo identifica bem os caminhantes e não identifica as árvores como caminhantes com muita frequência. No entanto, se a taxa de falsos positivos é muito alta, mas a taxa de falsos positivos também é muito alta, então o modelo é tendencioso; é identificar quase tudo o que encontra como caminhante. Da mesma forma, não queremos um modelo com uma baixa taxa de positividade verdadeira, porque então, quando o modelo encontra um caminhante, ele o rotula como uma árvore.

Curvas ROC

As curvas ROC (Receiver operator characteristic) são um gráfico onde traçamos a taxa de verdadeiro positivo versus a taxa de falso positivo.

As curvas ROC podem ser confusas para iniciantes por dois motivos principais. A primeira razão é que os iniciantes sabem que um modelo só tem um valor para taxas positivas verdadeiras e taxas negativas verdadeiras, então um gráfico ROC deve ser assim:

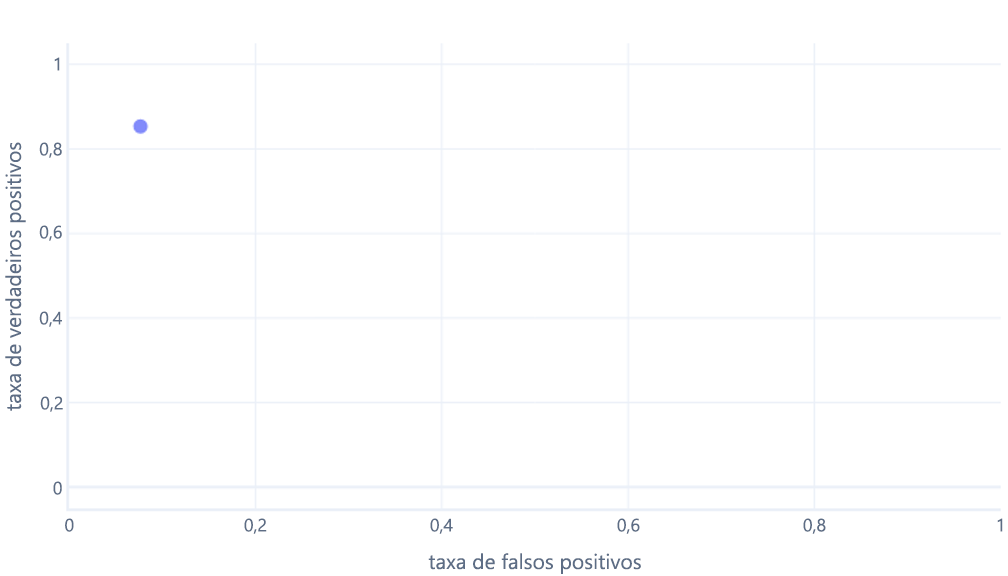
Se você também está pensando isso, você está certo. Um modelo treinado produz apenas um ponto. No entanto, lembre-se de que nossos modelos têm um limite – normalmente de 50% – que é usado para decidir se o rótulo verdadeiro (caminhante) ou falso (árvore) deve ser usado. Se alterarmos este limiar para 30% e recalcularmos as taxas de verdadeiros positivos e falsos positivos, obtemos outro ponto:

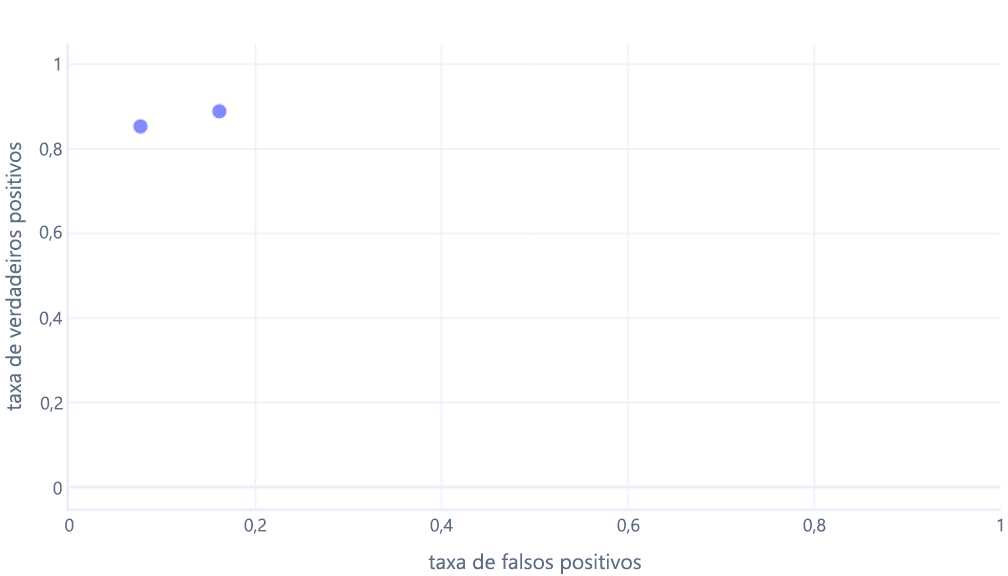
Se fizermos isso para limites entre 0% e 100%, podemos obter um gráfico como este:

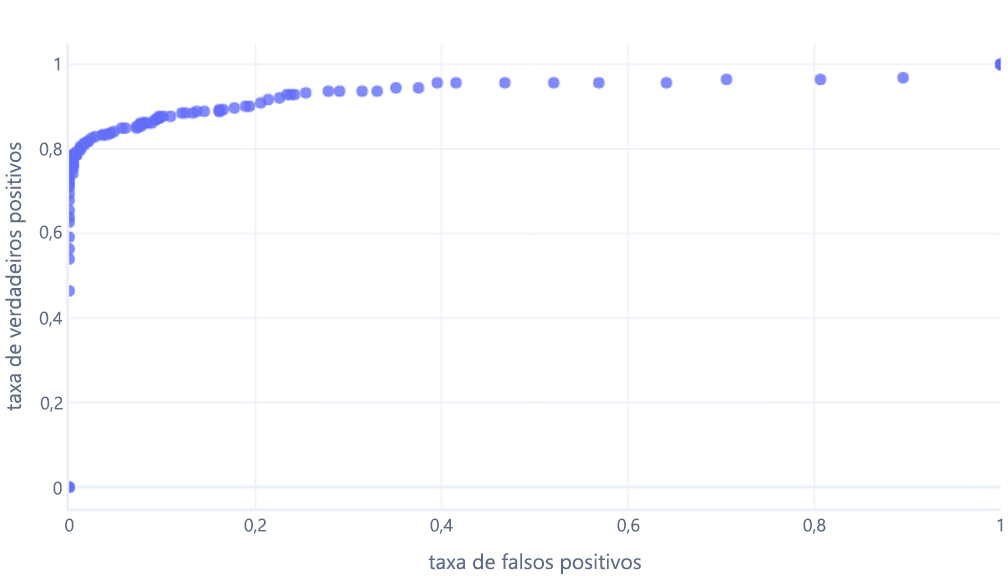
Que geralmente exibimos como uma linha, em vez disso:

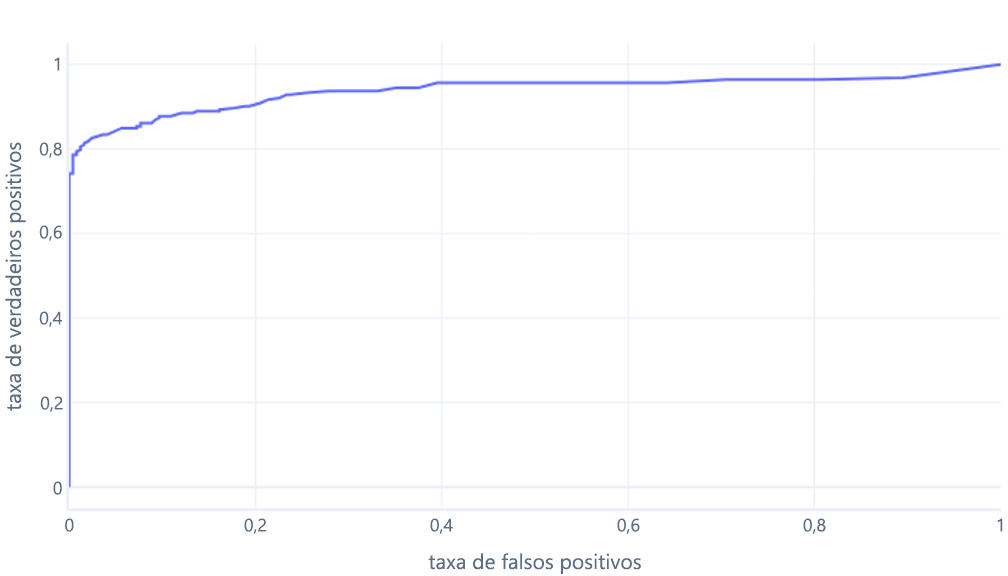
A segunda razão pela qual estes gráficos podem ser confusos é o jargão envolvido. Lembre-se que queremos uma alta taxa de verdadeiros positivos (identificando os caminhantes como tal) e uma baixa taxa de falsos positivos (não identificando árvores como caminhantes).

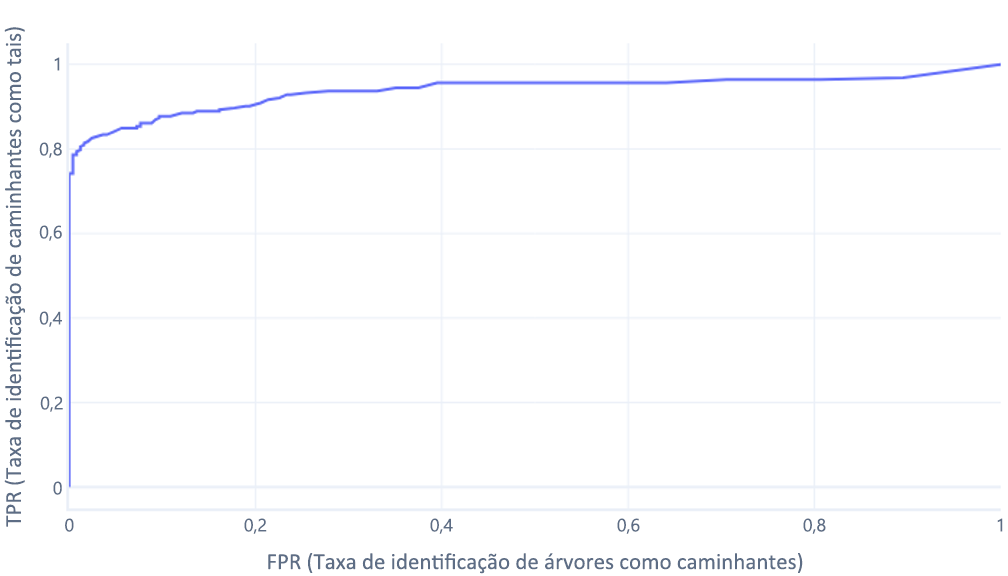
Bom ROC, mau ROC

Entender as curvas ROC boas e ruins é algo melhor feito em um ambiente interativo. Quando estiver pronto, vá para o próximo exercício para explorar este tópico.