Desequilíbrios de dados

  • 4 minutos

Quando nossos rótulos de dados têm mais de uma categoria do que de outra, dizemos que temos um desequilíbrio de dados. Por exemplo, lembre-se de que, em nosso cenário, estamos tentando identificar objetos encontrados por sensores de drones. Nossos dados são desequilibrados porque há números muito diferentes de caminhantes, animais, árvores e rochas em nossos dados de treinamento. Podemos ver isso tabulando estes dados:

Etiqueta Caminhante Animais Árvore Rock
Count 400 200 800 800

Ou traçando-o:

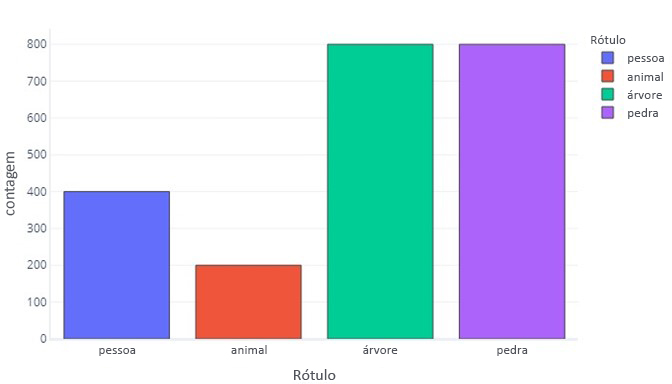
Gráfico de barras mostrando um número igual de rótulos de árvores e rochas, com menos rótulos de animais e pessoas.

Observe como a maioria dos dados são árvores ou rochas. Um conjunto de dados balanceado não tem esse problema.

Por exemplo, se estivéssemos tentando prever se um objeto é um caminhante, animal, árvore ou rocha, idealmente gostaríamos de ter um número igual de todas as categorias, assim:

Etiqueta Caminhante Animais Árvore Rock
Count 550 550 550 550

Se estivéssemos simplesmente tentando prever se um objeto era um caminhante, idealmente gostaríamos de ter um número igual de objetos caminhantes e não caminhantes:

Etiqueta Caminhante Não-Hiker
Count 1100 1100

Por que os desequilíbrios de dados são importantes?

Os desequilíbrios de dados são importantes porque os modelos podem aprender a imitar esses desequilíbrios quando não é desejável. Por exemplo, finja que treinamos um modelo de regressão logística para identificar objetos como caminhantes ou não. Se os dados de treinamento fossem fortemente dominados por rótulos de "caminhante", então o treinamento enviesaria o modelo para quase sempre retornar rótulos de "caminhante". No mundo real, porém, podemos descobrir que a maioria das coisas que os drones encontram são árvores. O modelo tendencioso provavelmente rotularia muitas dessas árvores como caminhantes.

Este fenómeno ocorre porque as funções de custo, por defeito, determinam se a resposta correta foi dada. Isso significa que, para um conjunto de dados tendencioso, a maneira mais simples de um modelo atingir o desempenho ideal pode ser ignorar virtualmente os recursos fornecidos e sempre, ou quase sempre, retornar a mesma resposta. Isto pode ter consequências devastadoras. Por exemplo, imagine que o nosso modelo de caminhante/não caminhante é treinado em dados onde apenas uma em cada 1000 amostras contém um caminhante. Um modelo que aprendeu a voltar "não-caminhante" todas as vezes tem uma precisão de 99,9%! Esta estatística parece ser excelente, mas o modelo é inútil porque nunca nos dirá se alguém está na montanha, e não saberemos resgatá-lo se uma avalanche atingir.

Enviesamento numa matriz de confusão

As matrizes de confusão são a chave para identificar desequilíbrios de dados ou enviesamento do modelo. Em um cenário ideal, os dados de teste têm um número aproximadamente par de rótulos, e as previsões feitas pelo modelo também são aproximadamente espalhadas pelos rótulos. Para 1000 amostras, um modelo imparcial, mas que muitas vezes obtém respostas erradas, pode parecer algo assim:

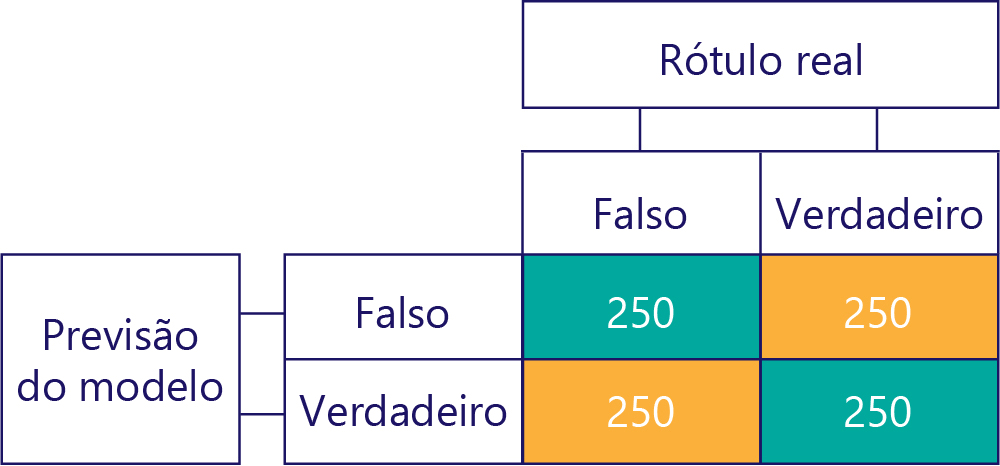
Diagrama de uma matriz de confusão simplificada com 250 para cada ponto de dados.

Podemos dizer que os dados de entrada são imparciais, porque as somas de linha são as mesmas (500 cada), indicando que metade dos rótulos são "verdadeiros" e metade são "falsos". Da mesma forma, podemos ver que o modelo está dando respostas imparciais porque está retornando verdadeiro metade do tempo e falso na outra metade do tempo.

Por outro lado, os dados tendenciosos contêm principalmente um tipo de rótulo, assim:

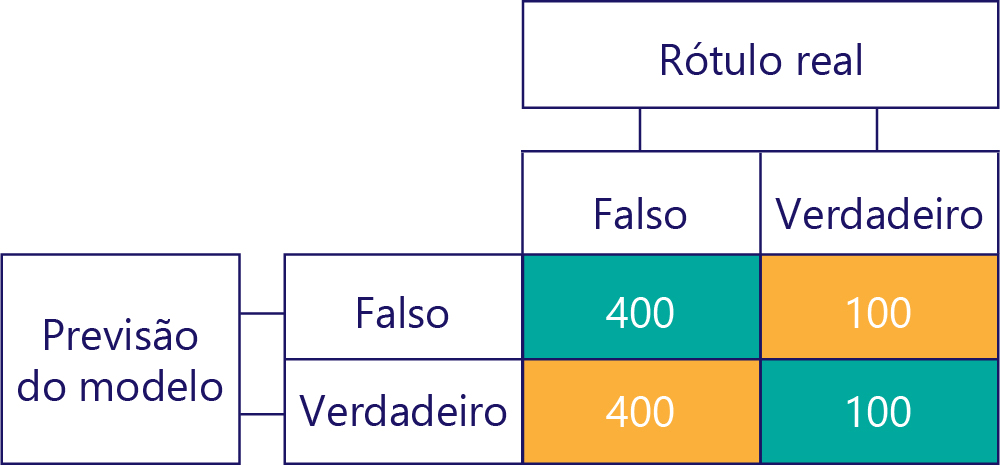
Diagrama de uma matriz de confusão simplificada com 400 para verdadeiros negativos, 100 para falsos negativos, 400 para falsos positivos e 100 para verdadeiros positivos.

Da mesma forma, um modelo tendencioso produz principalmente um tipo de rótulo, assim:

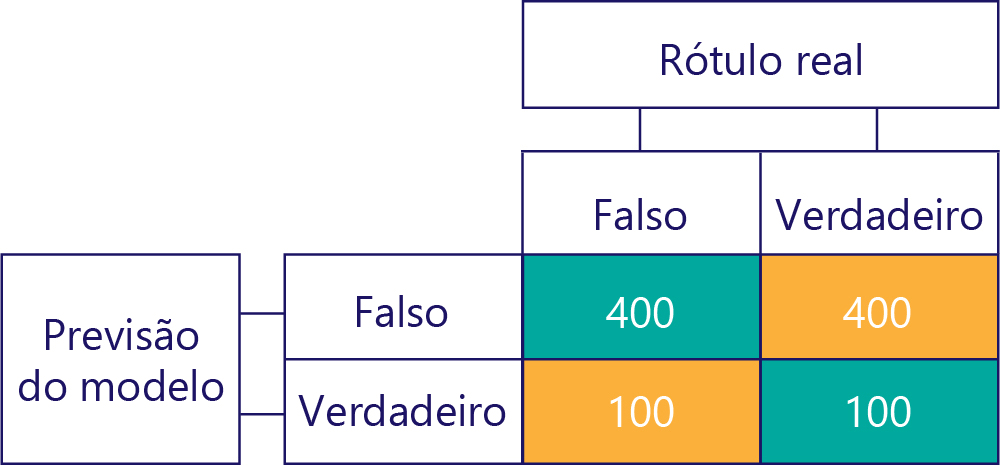
Diagrama de uma matriz de confusão simplificada com 400 para negativos verdadeiros, 400 para falsos negativos, 100 para falsos positivos e 100 para positivos verdadeiros.

Viés de modelo não é precisão

Lembre-se de que preconceito não é precisão. Por exemplo, alguns dos exemplos anteriores são tendenciosos e outros não, mas todos eles mostram um modelo que acerta a resposta 50% das vezes. Como um exemplo mais extremo, a matriz abaixo mostra um modelo imparcial que é impreciso:

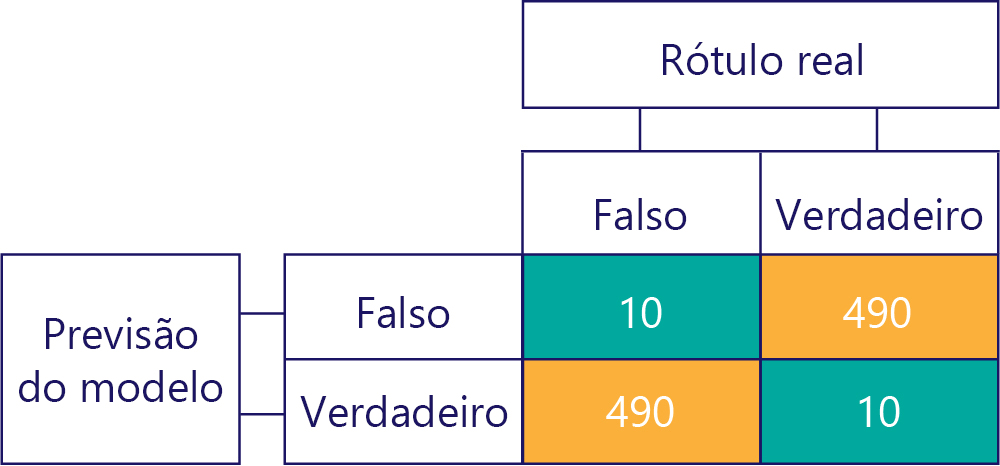
Diagrama de uma matriz de confusão simplificada com 10 para negativos verdadeiros, 490 para falsos negativos, 490 para falsos positivos e 10 para positivos verdadeiros.

Observe como o número de linhas e colunas é adicionado a 500, indicando que ambos os dados estão equilibrados e o modelo não está enviesado. Este modelo está recebendo quase todas as respostas incorretas, no entanto!

Claro, nosso objetivo é ter modelos precisos e imparciais, tais como:

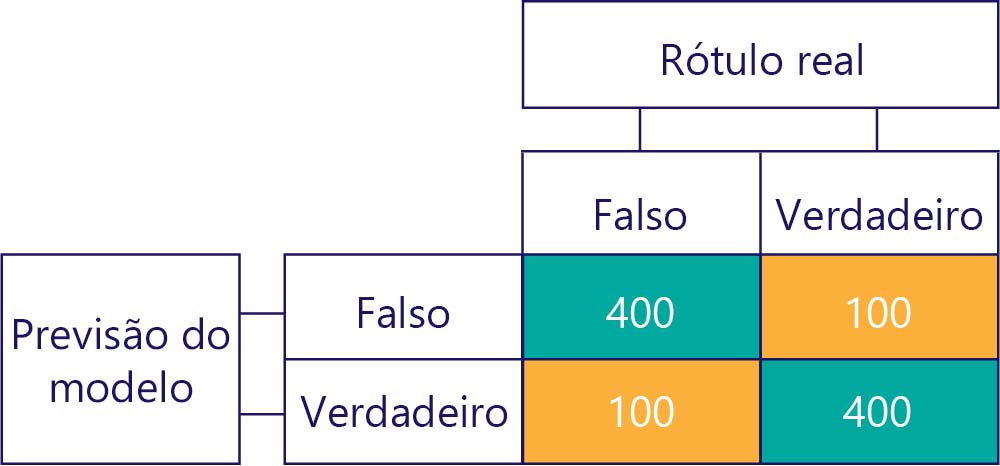
Diagrama de uma matriz de confusão simplificada com 400 para verdadeiros negativos, 100 para falsos negativos, 100 para falsos positivos e 400 para verdadeiros positivos.

… Mas precisamos garantir que nossos modelos precisos não sejam tendenciosos, simplesmente porque os dados são:

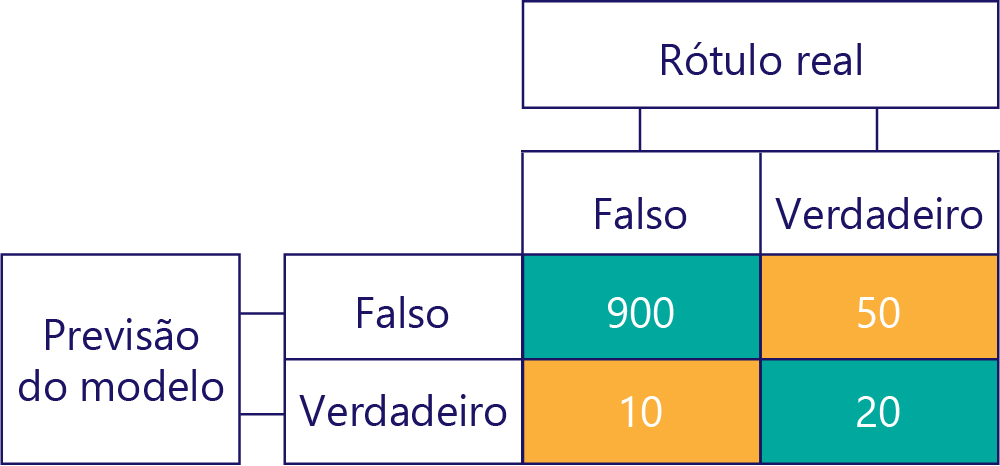
Diagrama de uma matriz de confusão simplificada com 900 para verdadeiros negativos, 50 para falsos negativos, 10 para falsos positivos e 20 para verdadeiros positivos.

Neste exemplo, observe como os rótulos reais são principalmente falsos (coluna da esquerda, mostrando um desequilíbrio de dados) e o modelo também retorna frequentemente false (linha superior, mostrando viés do modelo). Este modelo não é bom em dar corretamente respostas "Verdadeiras".

Evitar as consequências de dados desequilibrados

Algumas das maneiras mais simples de evitar as consequências de dados desequilibrados são:

  • Evite-o através de uma melhor seleção de dados.
  • "Reamostrar" seus dados para que eles contenham duplicatas da classe de rótulo minoritário.
  • Faça alterações na função de custo para que ela priorize rótulos menos comuns. Por exemplo, se a resposta errada for dada a Tree, a função de custo pode retornar 1; enquanto que se a resposta errada for feita para Hiker, ele pode retornar 10.

Exploraremos esses métodos no exercício a seguir.