Matrizes de confusão
Você pode pensar nos dados como contínuos, categóricos ou ordinais (categóricos, mas com uma ordem). As matrizes de confusão são um meio de avaliar o desempenho de um modelo categórico. Para contextualizar como eles funcionam, vamos primeiro atualizar nosso conhecimento sobre dados contínuos. Através disso, podemos ver como as matrizes de confusão são simplesmente uma extensão dos histogramas que já conhecemos.
Distribuições contínuas de dados
Quando queremos entender os dados contínuos, o primeiro passo geralmente é ver como eles são distribuídos. Considere o seguinte histograma:
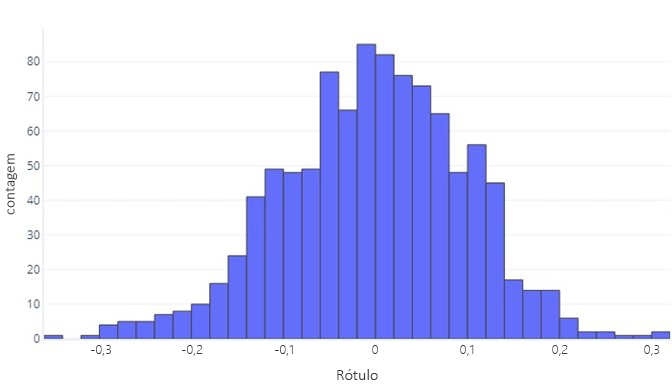
Podemos ver que o rótulo é, em média, cerca de zero, e a maioria dos pontos de dados situa-se entre -1 e 1. Apresenta-se como simétrica; há uma contagem aproximadamente uniforme de números menores e maiores do que a média. Se quiséssemos, poderíamos usar uma tabela em vez de um histograma, mas poderia ser pesado.
Distribuições categóricas de dados
Em alguns aspetos, os dados categóricos não são tão diferentes dos dados contínuos. Ainda podemos produzir histogramas para avaliar a frequência com que os valores aparecem para cada rótulo. Por exemplo, um rótulo binário (verdadeiro/falso) pode aparecer com frequência assim:
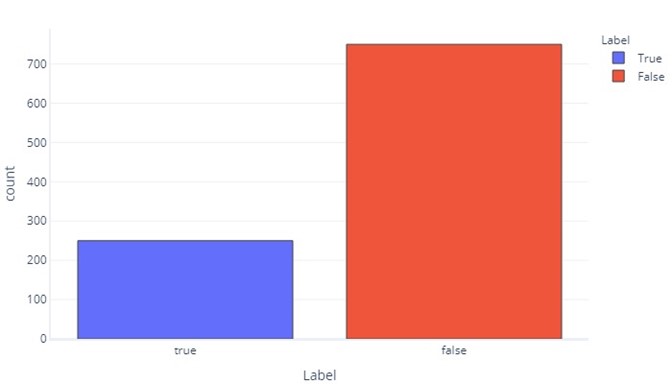
Isso nos diz que existem 750 amostras com "falso" como rótulo e 250 com "verdadeiro" como rótulo.
Um rótulo para três categorias é semelhante:
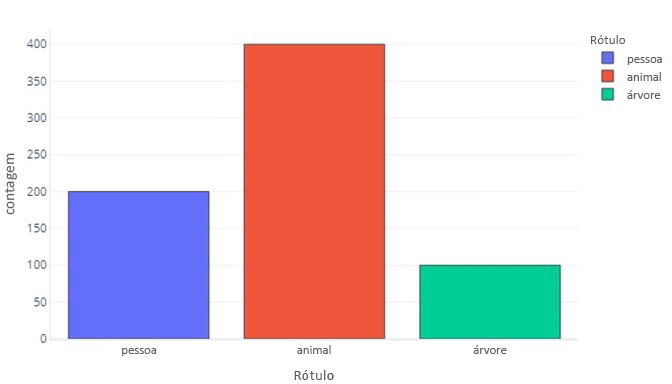
Isto diz-nos que há 200 amostras que são "pessoa", 400 que são "animais" e 100 que são "árvore".
Como os rótulos categóricos são mais simples, muitas vezes podemos mostrá-los como tabelas simples. Os dois gráficos anteriores parecem assim:
| Etiqueta | False | True |
|---|---|---|
| Count | 750 | 250 |
E:
| Etiqueta | Pessoa | Animais | Árvore |
|---|---|---|---|
| Count | 200 | 400 | 100 |
Olhando para as previsões
Podemos olhar para as previsões que o modelo faz da mesma forma que olhamos para os rótulos de verdade-base em nossos dados. Por exemplo, podemos ver que no conjunto de teste nosso modelo previu "falso" 700 vezes e "verdadeiro" 300 vezes.
| Previsão do modelo | Count |
|---|---|
| False | 700 |
| True | 300 |
Isso fornece informações diretas sobre as previsões que nosso modelo está fazendo, mas não nos diz quais delas estão corretas. Embora possamos usar uma função de custo para entender com que frequência as respostas corretas são dadas, a função de custo não nos informará quais tipos de erros estão sendo cometidos. Por exemplo, o modelo pode adivinhar corretamente todos os valores "verdadeiros", mas também adivinhar "verdadeiro" quando deveria ter adivinhado "falso".
A matriz da confusão
A chave para entender o desempenho do modelo é combinar a tabela para previsão do modelo com a tabela para rótulos de dados de verdade básica:
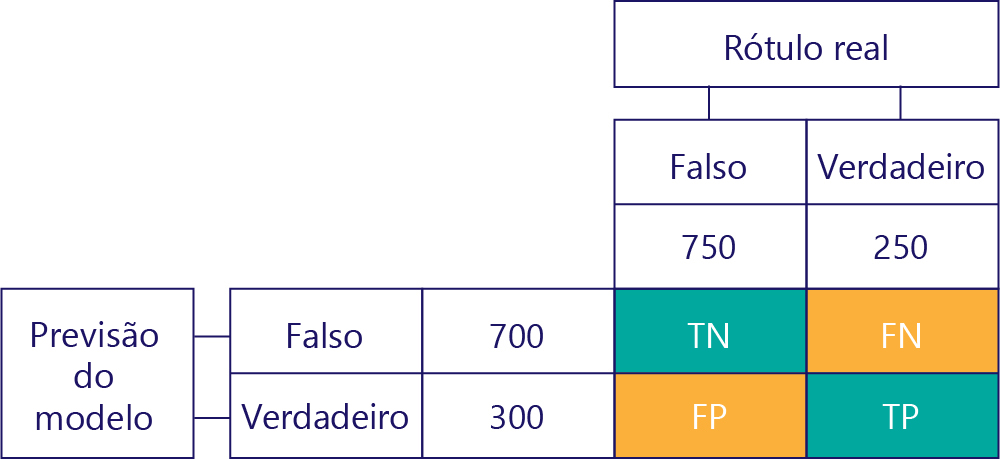
O quadrado que não preenchemos chama-se matriz da confusão.
Cada célula na matriz de confusão nos diz uma coisa sobre o desempenho do modelo. Estes são Verdadeiros Negativos (TN), Falso Negativos (FN), Falso Positivos (FP) e Verdadeiros Positivos (TP).
Vamos explicá-las uma a uma, substituindo essas siglas por valores reais. Quadrados azul-esverdeados significam que o modelo fez uma previsão correta, e quadrados laranja significam que o modelo fez uma previsão incorreta.
Verdadeiros Negativos (TN)
O valor superior esquerdo listará quantas vezes o modelo previu falso, e o rótulo real também era falso. Em outras palavras, isso lista quantas vezes o modelo previu corretamente falso. Digamos, por exemplo, que isso aconteceu 500 vezes:

Falsos Negativos (FN)
O valor superior direito nos diz quantas vezes o modelo previu falso, mas o rótulo real era verdadeiro. Sabemos agora que são 200. Como? Porque o modelo previu falso 700 vezes, e 500 dessas vezes o fez corretamente. Assim, 200 vezes deve ter previsto falso quando não deveria.

Falsos Positivos (FP)
O valor inferior esquerdo contém falsos positivos. Isso nos diz quantas vezes o modelo previu verdadeiro, mas o rótulo real era falso. Sabemos agora que são 250, porque houve 750 vezes que a resposta correta era falsa. 500 destas vezes aparecem na célula superior esquerda (TN):
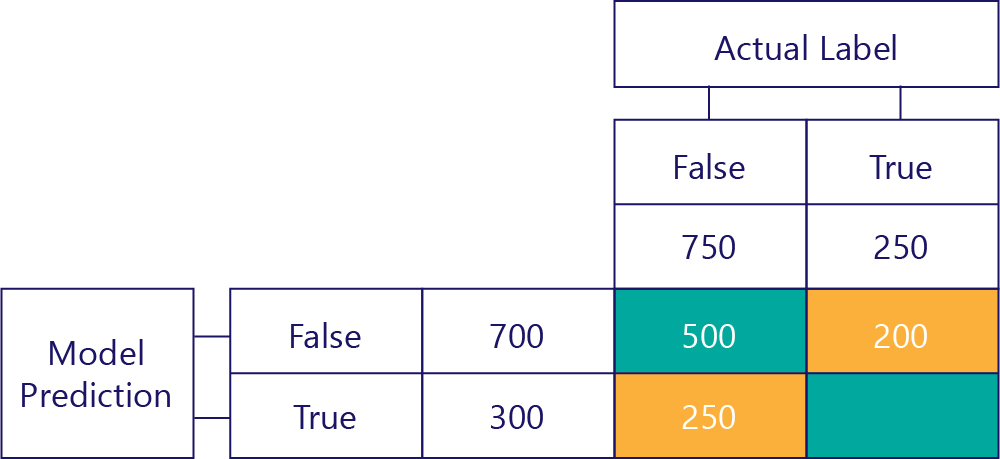
Verdadeiros Positivos (TP)
Finalmente, temos verdadeiros pontos positivos. Este é o número de vezes que o modelo prevê corretamente a verdade. Sabemos que são 50 por duas razões. Em primeiro lugar, o modelo previu a verdade 300 vezes, mas 250 vezes estava incorreta (célula inferior esquerda). Em segundo lugar, havia 250 vezes que verdadeiro era a resposta correta, mas 200 vezes o modelo previa falso.
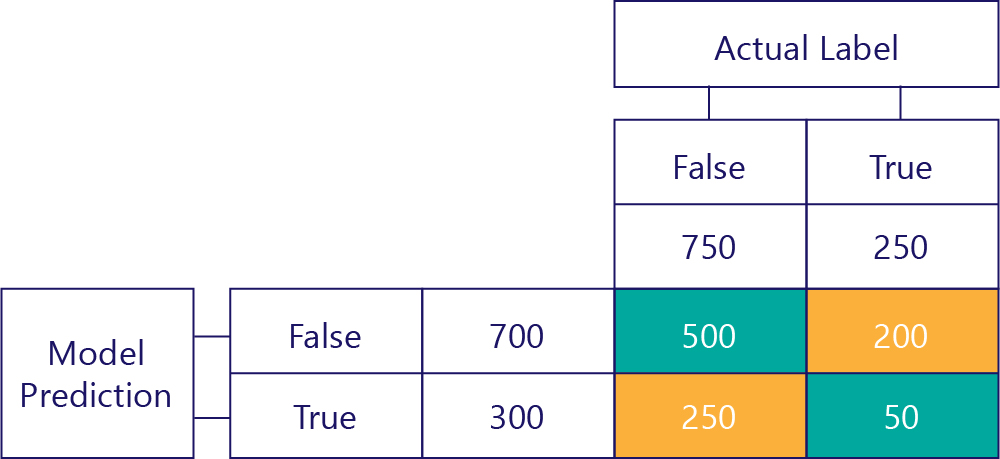
A matriz final
Normalmente, simplificamos um pouco a nossa matriz de confusão, assim:
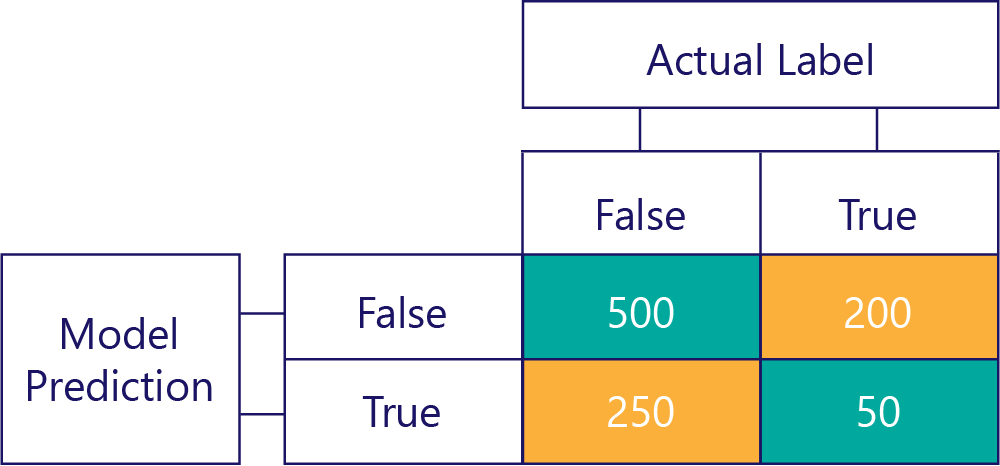
Colorimos as células aqui para destacar quando o modelo fez previsões corretas. A partir disso, sabemos não apenas quantas vezes o modelo fez certos tipos de previsões, mas também quantas vezes essas previsões estavam corretas ou incorretas.
Matrizes de confusão também podem ser construídas quando há mais rótulos. Por exemplo, para o nosso exemplo de pessoa/animal/árvore, podemos obter uma matriz assim:
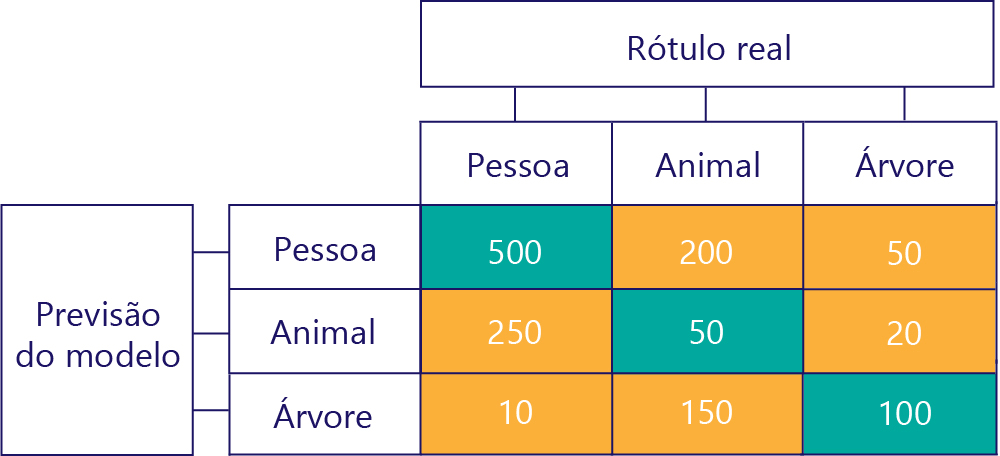
Quando há três categorias, métricas como True Positives não se aplicam mais, mas ainda podemos ver exatamente com que frequência o modelo cometeu certos tipos de erros. Por exemplo, podemos ver que o modelo previu que "pessoa" 200 vezes quando o resultado real correto era "animal".