Otimizar modelos usando descida de gradiente

  • 6 minutos

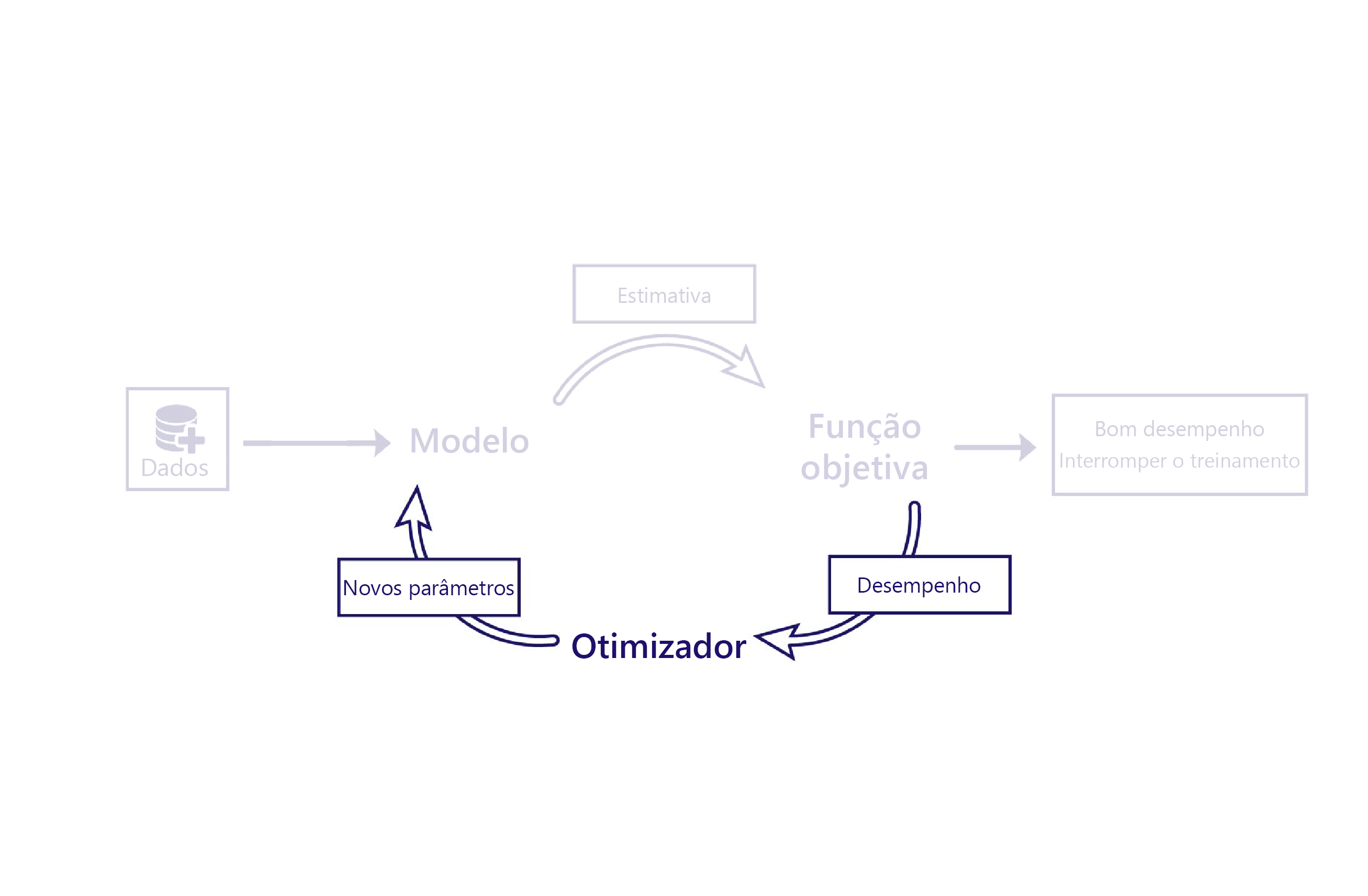
Vimos como as funções de custo avaliam o desempenho dos modelos usando dados. O otimizador é a peça final do quebra-cabeça.

O papel do otimizador é alterar o modelo de forma a melhorar o seu desempenho. Ele faz essa alteração inspecionando as saídas e o custo do modelo e sugerindo novos parâmetros para o modelo.

Por exemplo, em nosso cenário agrícola, nosso modelo linear tem dois parâmetros: o interceto da linha e a inclinação da linha. Se a intercetação da linha estiver errada, o modelo subestima ou superestima as temperaturas em média. Se a inclinação estiver errada, o modelo não faz um bom trabalho ao demonstrar como as temperaturas têm mudado desde a década de 1950. O otimizador altera esses dois parâmetros para que eles façam um trabalho ideal de modelagem de temperaturas ao longo do tempo.

Diagrama que mostra a parte do otimizador do ciclo de vida do aprendizado de máquina.

Gradiente descendente

O algoritmo de otimização mais comum atualmente é a descida de gradiente. Existem várias variantes deste algoritmo, mas todas usam os mesmos conceitos centrais.

A descida de gradiente usa o cálculo para estimar como a alteração de cada parâmetro altera o custo. Por exemplo, o aumento de um parâmetro pode ser previsto para reduzir o custo.

A descida de gradiente é nomeada como tal porque calcula o gradiente (inclinação) da relação entre cada parâmetro do modelo e o custo. Os parâmetros são então alterados para descer esta encosta.

Este algoritmo é simples e poderoso, mas não é garantido encontrar os parâmetros ideais do modelo que minimizam o custo. As duas principais fontes de erro são os mínimos locais e a instabilidade.

Mínimos locais

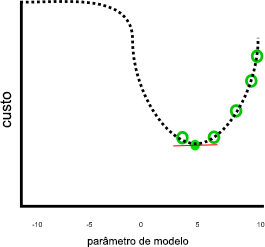
Nosso exemplo anterior parecia fazer um bom trabalho, assumindo que o custo continuaria aumentando quando o parâmetro fosse menor que 0 ou maior que 10:

Gráfico de custo versus parâmetro do modelo, com um mínimo para o custo quando o parâmetro do modelo é cinco.

Esse trabalho não pareceria ser tão grande se parâmetros menores que zero ou maiores que 10 resultassem em custos mais baixos, como nesta imagem:

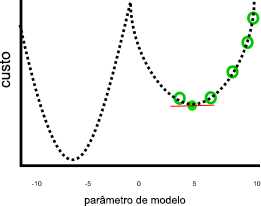
Gráfico de custo versus parâmetro do modelo, com um mínimo local para o custo quando o parâmetro do modelo é cinco, mas um custo menor quando o parâmetro do modelo está em seis negativos.

No gráfico anterior, um valor de parâmetro de sete negativos seria uma solução melhor do que cinco, porque tem um custo menor. A descida de gradiente não conhece a relação completa entre cada parâmetro e o custo — representado pela linha pontilhada — com antecedência. Portanto, é propenso a encontrar mínimos locais: estimativas de parâmetros que não são a melhor solução, mas o gradiente é zero.

Instabilidade

Uma questão relacionada é que a descida de gradiente às vezes mostra instabilidade. Essa instabilidade geralmente ocorre quando o tamanho da etapa ou a taxa de aprendizado — a quantidade que cada parâmetro é ajustado por cada iteração — é muito grande. Os parâmetros são então ajustados muito longe em cada etapa, e o modelo realmente piora a cada iteração:

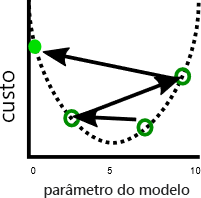
Gráfico de custo versus parâmetro do modelo, que mostra o custo se movendo em grandes etapas com redução mínima no custo.

Ter uma taxa de aprendizagem mais lenta pode resolver este problema, mas também pode introduzir problemas. Em primeiro lugar, taxas de aprendizagem mais lentas podem significar que a formação demora muito tempo, porque são necessárias mais etapas. Em segundo lugar, dar passos menores torna mais provável que o treinamento se estabeleça em um mínimo local:

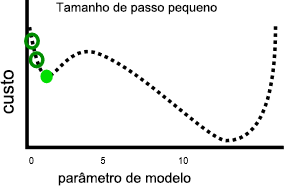
Gráfico de custo versus parâmetro do modelo, mostrando pequenos movimentos no custo.

Por outro lado, uma taxa de aprendizagem mais rápida pode tornar mais fácil evitar atingir mínimos locais, porque etapas maiores podem ignorar os máximos locais:

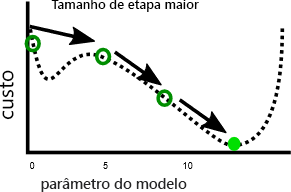
Gráfico de custo versus parâmetro do modelo, com movimentos regulares no custo até que um mínimo seja atingido.

Como veremos no próximo exercício, há um tamanho de passo ideal para cada problema. Encontrar este ótimo é algo que muitas vezes requer experimentação.