Exercício - Explore fatias

12 minutos

Exploramos matrizes na seção anterior e aprendemos que matrizes são a base para fatias e mapas. Você vai entender o porquê em um momento. Como matrizes, uma fatia é um tipo de dados em Go que representa uma sequência de elementos do mesmo tipo. Mas a diferença mais significativa com matrizes é que o tamanho de uma fatia é dinâmico, não fixo.

Uma fatia é uma estrutura de dados sobre uma matriz ou outra fatia. Referimo-nos à matriz ou fatia de origem como a matriz subjacente. Com uma fatia, você pode acessar toda a matriz subjacente ou apenas uma subsequência de elementos.

Uma fatia tem apenas três componentes:

Ponteiro para o primeiro elemento acessível da matriz subjacente. Este elemento não é necessariamente o primeiro elemento da matriz, array[0].
Comprimento da fatia. O número de elementos na fatia.
Capacidade da fatia. O número de elementos entre o início da fatia e o final da matriz subjacente.

A imagem a seguir representa o que é uma fatia:

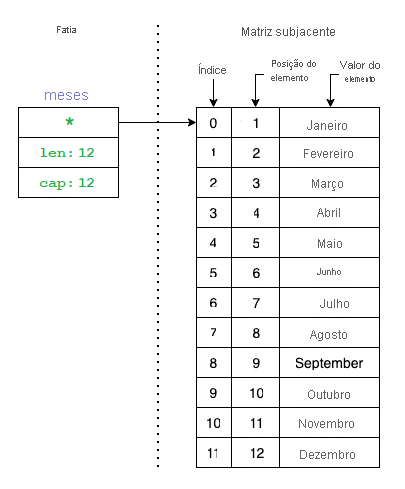
Diagrama mostrando a aparência das fatias em Go.

Observe como a fatia é apenas um subconjunto da matriz subjacente. Vamos ver como você pode representar a imagem anterior no código.

Declarar e inicializar uma fatia

Para declarar uma fatia, faça-o da mesma forma que declara uma matriz. Por exemplo, o código a seguir representa o que você viu na imagem de fatia:

package main

import "fmt"

func main() {
    months := []string{"January", "February", "March", "April", "May", "June", "July", "August", "September", "October", "November", "December"}
    fmt.Println(months)
    fmt.Println("Length:", len(months))
    fmt.Println("Capacity:", cap(months))
}

Quando você executa o código, você vê a seguinte saída:

[January February March April May June July August September October November December]
Length: 12
Capacity: 12

Observe como, no momento, uma fatia não difere muito de uma matriz. Declara-os da mesma forma. Para obter as informações de uma fatia, você pode usar as funções len() internas e cap(). Continuaremos usando essas funções para confirmar que uma fatia pode ter uma subsequência de elementos de uma matriz subjacente.

Itens de fatia

Go tem suporte para o operador s[i:p]de fatia, onde:

s representa a matriz.
i Representa o ponteiro para o primeiro elemento da matriz subjacente (ou outra fatia) a ser adicionado à nova fatia. A variável i corresponde ao elemento no local i do índice na matriz, array[i]. Lembre-se de que esse elemento não é necessariamente o primeiro elemento da matriz subjacente, array[0].
p representa o número de elementos na matriz subjacente a serem usados ao criar a nova fatia e também a posição do elemento. A variável p corresponde ao último elemento na matriz subjacente que pode ser usado na nova fatia. O elemento em posição p na matriz subjacente é encontrado no local array[i+1]. Observe que esse elemento não é necessariamente o último elemento da matriz subjacente, array[len(array)-1].

Portanto, uma fatia poderia se referir apenas a um subconjunto de elementos.

Digamos que você queira quatro variáveis para representar cada trimestre do ano, e você tem uma fatia de months com 12 elementos. A imagem a seguir ilustra como fatiar months em quatro novas quarter fatias:

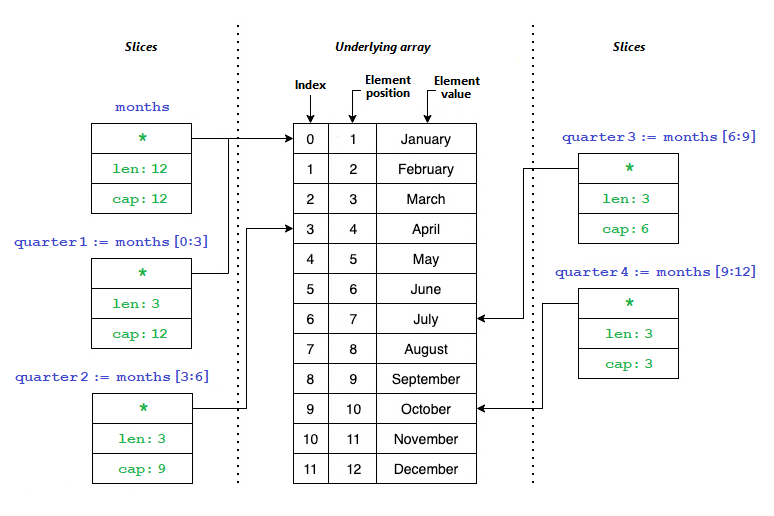
Diagrama mostrando a aparência de várias fatias em Go.

Para representar em código o que você viu na imagem anterior, você pode usar o seguinte código:

package main

import "fmt"

func main() {
    months := []string{"January", "February", "March", "April", "May", "June", "July", "August", "September", "October", "November", "December"}
    quarter1 := months[0:3]
    quarter2 := months[3:6]
    quarter3 := months[6:9]
    quarter4 := months[9:12]
    fmt.Println(quarter1, len(quarter1), cap(quarter1))
    fmt.Println(quarter2, len(quarter2), cap(quarter2))
    fmt.Println(quarter3, len(quarter3), cap(quarter3))
    fmt.Println(quarter4, len(quarter4), cap(quarter4))
}

Quando você executa o código, você obtém a seguinte saída:

[January February March] 3 12
[April May June] 3 9
[July August September] 3 6
[October November December] 3 3

Observe como o comprimento das fatias é o mesmo, mas a capacidade é diferente. Vamos explorar a quarter2 fatia. Quando você declara essa fatia, está dizendo que deseja que a fatia comece na posição número três, e o último elemento está localizado na posição número seis. O comprimento da fatia é de três elementos, mas a capacidade é nove porque a matriz subjacente tem mais elementos ou posições disponíveis, mas não visíveis para a fatia. Por exemplo, se você tentar imprimir algo como fmt.Println(quarter2[3]), receberá o seguinte erro: panic: runtime error: index out of range [3] with length 3.

A capacidade de uma fatia diz apenas o quanto você pode estender uma fatia. Por esse motivo, você pode criar uma fatia estendida do quarter2, como este exemplo:

package main

import "fmt"

func main() {
    months := []string{"January", "February", "March", "April", "May", "June", "July", "August", "September", "October", "November", "December"}
    quarter2 := months[3:6]
    quarter2Extended := quarter2[:4]
    fmt.Println(quarter2, len(quarter2), cap(quarter2))
    fmt.Println(quarter2Extended, len(quarter2Extended), cap(quarter2Extended))
}

Quando você executa o código anterior, você obtém a seguinte saída:

[April May June] 3 9
[April May June July] 4 9

Observe que, ao declarar a quarter2Extended variável, não é necessário especificar a posição inicial ([:4]). Quando você faz isso, Go assume que você quer a primeira posição da fatia. Você pode fazer o mesmo para a última posição ([1:]). Go assumirá que você deseja fazer referência a todos os elementos até a última posição de uma fatia (len()-1).

Acrescentar itens

Exploramos como as fatias funcionam e como elas são semelhantes às matrizes. Agora vamos descobrir como eles diferem dos arrays. A primeira diferença é que o tamanho de uma fatia não é fixo, é dinâmico. Depois de criar uma fatia, você pode adicionar mais elementos a ela e a fatia será estendida. Você verá em um momento o que acontece com a matriz subjacente.

Para adicionar um elemento a uma fatia, o Go oferece a append(slice, element) função integrada. Você passa a fatia para modificar e o elemento para acrescentar como valores para a função. Em seguida, a append função retorna uma nova fatia que você armazena em uma variável. Pode ser a mesma variável para a fatia que você está mudando.

Vamos ver como o processo de acréscimo parece no código:

package main

import "fmt"

func main() {
    var numbers []int
    for i := 0; i < 10; i++ {
        numbers = append(numbers, i)
        fmt.Printf("%d\tcap=%d\t%v\n", i, cap(numbers), numbers)
    }
}

Quando você executa o código anterior, você deve ver a seguinte saída:

0       cap=1   [0]
1       cap=2   [0 1]
2       cap=4   [0 1 2]
3       cap=4   [0 1 2 3]
4       cap=8   [0 1 2 3 4]
5       cap=8   [0 1 2 3 4 5]
6       cap=8   [0 1 2 3 4 5 6]
7       cap=8   [0 1 2 3 4 5 6 7]
8       cap=16  [0 1 2 3 4 5 6 7 8]
9       cap=16  [0 1 2 3 4 5 6 7 8 9]

Esta saída é interessante. Especialmente para o que a chamada para a cap() função está retornando. Tudo parece normal até a terceira iteração, onde a capacidade muda para 4, e há apenas três elementos na fatia. Na quinta iteração, a capacidade varia novamente para 8 e na nona para 16.

Você percebe um padrão na saída de capacidade? Quando uma fatia não tem capacidade suficiente para conter mais elementos, o Go duplica a sua capacidade. Ele cria uma nova matriz subjacente com a nova capacidade. Não é preciso fazer nada para que esse aumento de capacidade aconteça. Go faz isso automaticamente. É preciso ser cauteloso. Em algum momento, uma fatia pode ter muito mais capacidade do que precisa, e você estará desperdiçando memória.

Remover itens

Você deve estar se perguntando, que tal remover elementos? Bem, o Go não tem uma função interna para remover elementos de uma fatia. Você pode usar o operador s[i:p] de fatia que abordamos anteriormente para criar uma nova fatia com apenas os elementos necessários.

Por exemplo, o código a seguir remove um elemento de uma fatia:

package main

import "fmt"

func main() {
    letters := []string{"A", "B", "C", "D", "E"}
    remove := 2

	if remove < len(letters) {

		fmt.Println("Before", letters, "Remove ", letters[remove])

		letters = append(letters[:remove], letters[remove+1:]...)

		fmt.Println("After", letters)
	}

}

Quando você executa o código anterior, você obtém a seguinte saída:

Before [A B C D E] Remove  C
After [A B D E]

Este código remove um elemento de uma fatia. Ele substitui o elemento a ser removido pelo próximo elemento na fatia, ou nenhum se você estiver removendo o último elemento.

Outra abordagem é criar uma nova cópia da fatia. Aprenderemos como fazer cópias de fatias na próxima seção.

Criar cópias de fatias

O Go tem uma função integrada copy(dst, src []Type) para criar cópias de uma fatia. Você envia a fatia de destino e a fatia de origem. Por exemplo, você pode criar uma cópia de uma fatia como este exemplo mostra:

slice2 := make([]string, 3)
copy(slice2, letters[1:4])

Por que você se preocuparia em criar cópias? Bem, quando você altera um elemento de uma fatia, você também está alterando a matriz subjacente. Quaisquer outras fatias que se refiram à mesma matriz subjacente serão afetadas. Vamos ver esse processo no código e, em seguida, vamos corrigi-lo criando uma cópia de uma fatia.

Use o código a seguir para confirmar se uma fatia aponta para uma matriz e cada alteração feita em uma fatia afeta a matriz subjacente.

package main

import "fmt"

func main() {
    letters := []string{"A", "B", "C", "D", "E"}
    fmt.Println("Before", letters)

    slice1 := letters[0:2]
    slice2 := letters[1:4]

    slice1[1] = "Z"

    fmt.Println("After", letters)
    fmt.Println("Slice2", slice2)
}

Quando você executa o código anterior, você vê a seguinte saída:

Before [A B C D E]
After [A Z C D E]
Slice2 [Z C D]

Observe como a alteração que fizemos no slice1 afetou o array e slice2o letters . Você pode ver na saída que a letra B foi substituída por Z, e isso afeta todos que estão apontando para a letters matriz.

Para corrigir esse problema, você precisa criar uma cópia de fatia, que sob o capô faz uma nova matriz subjacente. Você pode usar o seguinte código:

package main

import "fmt"

func main() {
    letters := []string{"A", "B", "C", "D", "E"}
    fmt.Println("Before", letters)

    slice1 := letters[0:2]

    slice2 := make([]string, 3)
    copy(slice2, letters[1:4])

    slice1[1] = "Z"

    fmt.Println("After", letters)
    fmt.Println("Slice2", slice2)
}