Aprendizagem aprofundada

Concluído

A aprendizagem profunda é uma forma avançada de machine learning que tenta imitar a forma como o cérebro humano aprende. A chave para a aprendizagem profunda é a criação de uma rede neural artificial que simula a atividade electroquímica em neurónios biológicos utilizando funções matemáticas, como mostrado aqui.

Rede neural biológica	Rede neural artificial
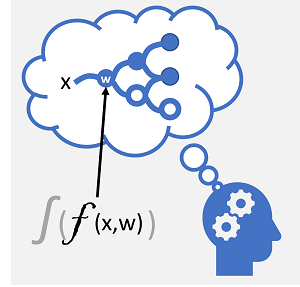
Os neurónios disparam em resposta aos estímulos electroquímicos. Quando disparado, o sinal é transmitido aos neurónios ligados.	Cada neurónio é uma função que opera com um valor de entrada (x) e um peso (w). A função é encapsulada numa função de ativação que determina se deve transmitir a saída.

As redes neurais artificiais são compostas por múltiplas camadas de neurónios - essencialmente definindo uma função profundamente aninhada. Esta arquitetura é a razão pela qual a técnica é referida como aprendizagem profunda e os modelos produzidos por ela são frequentemente referidos como redes neurais profundas (DNNs). Pode utilizar redes neurais profundas para muitos tipos de problemas de machine learning, incluindo regressão e classificação, bem como modelos mais especializados para processamento de linguagem natural e imagem digitalizada.

Tal como outras técnicas de machine learning abordadas neste módulo, a aprendizagem profunda envolve ajustar os dados de preparação a uma função que pode prever uma etiqueta (y) com base no valor de uma ou mais funcionalidades (x). A função (f(x)) é a camada externa de uma função aninhada na qual cada camada da rede neural encapsula funções que operam em x e os valores de peso (w) associados às mesmas. O algoritmo utilizado para preparar o modelo envolve alimentar iterativamente os valores da funcionalidade (x) nos dados de preparação para a frente através das camadas para calcular os valores de saída de ³, validando o modelo para avaliar a distância entre os valores calculados ΰ dos valores conhecidos de y (que quantifica o nível de erro ou perda no modelo), e, em seguida, modificar os pesos (w) para reduzir a perda. O modelo preparado inclui os valores de peso final que resultam nas predições mais precisas.

Exemplo – Utilizar a aprendizagem profunda para classificação

Para compreender melhor como funciona um modelo de rede neural profundo, vamos explorar um exemplo em que uma rede neural é utilizada para definir um modelo de classificação para espécies de pinguins.

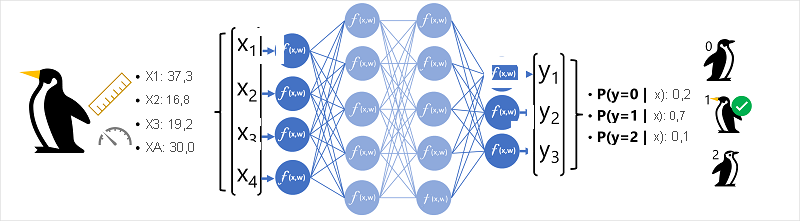
Os dados da funcionalidade (x) consistem em algumas medidas de um pinguim. Especificamente, as medidas são:

• O comprimento da conta do pinguim.
• A profundidade da conta do pinguim.
• O comprimento das flippers do pinguim.
• O peso do pinguim.

Neste caso, x é um vetor de quatro valores ou matematicamente, x=[x1,x2,x3,x4].

O rótulo que estamos a tentar prever (y) é a espécie do pinguim, e que existem três espécies possíveis que podem ser:

• Adélia
• Gentoo
• Chinstrap

Este é um exemplo de um problema de classificação, no qual o modelo de machine learning tem de prever a classe mais provável à qual pertence uma observação. Um modelo de classificação consegue isto ao prever uma etiqueta que consiste na probabilidade de cada classe. Por outras palavras, y é um vetor de três valores de probabilidade; uma para cada uma das classes possíveis: [P(y=0|x), P(y=1|x), P(y=2|x)].

O processo para inferir uma classe de pinguins prevista com esta rede é:

1. O vetor de funcionalidade para uma observação de pinguins é inserido na camada de entrada da rede neural, que consiste num neurónio para cada valor x . Neste exemplo, o vetor x seguinte é utilizado como entrada: [37.3, 16.8, 19.2, 30.0]
2. As funções para a primeira camada de neurónios calculam uma soma ponderada ao combinar o valor x e o peso w e transmitem-no a uma função de ativação que determina se cumpre o limiar a ser transmitido para a camada seguinte.
3. Cada neurónio numa camada está ligado a todos os neurónios na camada seguinte (uma arquitetura por vezes chamada rede totalmente ligada) para que os resultados de cada camada sejam alimentados para a frente através da rede até chegarem à camada de saída.
4. A camada de saída produz um vetor de valores; neste caso, utilizar uma função softmax ou semelhante para calcular a distribuição de probabilidade para as três classes possíveis de pinguins. Neste exemplo, o vetor de saída é: [0.2, 0.7, 0.1]
5. Os elementos do vetor representam as probabilidades das classes 0, 1 e 2. O segundo valor é o mais alto, pelo que o modelo prevê que a espécie do pinguim é 1 (Gentoo).

Como aprende uma rede neural?

Os pesos numa rede neural são centrais na forma como calcula os valores previstos para as etiquetas. Durante o processo de preparação, o modelo aprende os pesos que resultarão nas predições mais precisas. Vamos explorar o processo de preparação com um pouco mais de detalhe para compreender como esta aprendizagem ocorre.

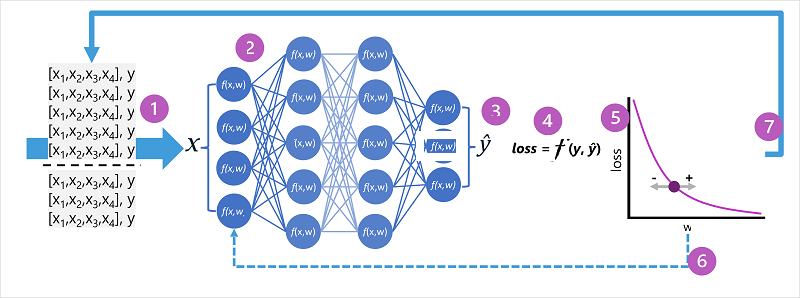
1. Os conjuntos de dados de preparação e validação são definidos e as funcionalidades de preparação são inseridas na camada de entrada.
2. Os neurónios em cada camada da rede aplicam os seus pesos (que são inicialmente atribuídos aleatoriamente) e alimentam os dados através da rede.
3. A camada de saída produz um vetor que contém os valores calculados para ^. Por exemplo, uma saída para uma predição de classe de pinguins pode ser [0,3. 0.1. 0.6].
4. Uma função de perda é utilizada para comparar os valores previstos com os valores y conhecidos e agregar a diferença (que é conhecida como perda). Por exemplo, se a classe conhecida para o caso que devolveu o resultado no passo anterior for Chinstrap, o valor y deve ser [0,0, 0,0, 1,0]. A diferença absoluta entre este e o vetor é[0.3, 0.1, 0.4]. Na realidade, a função de perda calcula a variância agregada para vários casos e resume-a como um valor de perda único.
5. Uma vez que toda a rede é essencialmente uma grande função aninhada, uma função de otimização pode utilizar cálculo diferencial para avaliar a influência de cada peso na rede na perda e determinar como podem ser ajustadas (para cima ou para baixo) para reduzir a quantidade de perda global. A técnica de otimização específica pode variar, mas geralmente envolve uma abordagem descendente de gradação em que cada peso é aumentado ou diminuído para minimizar a perda.
6. As alterações aos pesos são colocadas novamente em frente às camadas na rede, substituindo os valores utilizados anteriormente.
7. O processo é repetido em várias iterações ( conhecidas como épocas) até que a perda seja minimizada e o modelo preveja com precisão aceitável.

Nota

Embora seja mais fácil pensar em cada caso nos dados de preparação que estão a ser transmitidos através da rede um de cada vez, na realidade os dados são colocados em lotes em matrizes e processados através de cálculos algebraicos lineares. Por este motivo, a preparação da rede neural é realizada melhor em computadores com unidades de processamento gráfico (GPUs) otimizadas para manipulação de vetores e matrizes.