Classificação binária
A classificação, assim como a regressão, é uma técnica supervisionada de aprendizado de máquina e, portanto, segue o mesmo processo iterativo de treinamento, validação e avaliação de modelos. Em vez de calcular valores numéricos como um modelo de regressão, os algoritmos usados para treinar modelos de classificação calculam valores de probabilidade para atribuição de classe e as métricas de avaliação usadas para avaliar o desempenho do modelo comparam as classes previstas com as classes reais.
Algoritmos de classificação binária são usados para treinar um modelo que prevê um dos dois rótulos possíveis para uma única classe. Essencialmente, prevendo verdadeiro ou falso. Na maioria dos cenários reais, as observações de dados usadas para treinar e validar o modelo consistem em vários valores de feição (x) e um valor y que é 1 ou 0.
Exemplo - classificação binária
Para entender como funciona a classificação binária, vejamos um exemplo simplificado que usa um único recurso (x) para prever se o rótulo y é 1 ou 0. Neste exemplo, vamos usar o nível de glicose no sangue de um paciente para prever se o paciente tem ou não diabetes. Aqui estão os dados com os quais treinaremos o modelo:
 |
 |
|---|---|
| Glicose no sangue (x) | Diabético? y) |
| 67 | 0 |
| 103 | 1 |
| 114 | 1 |
| 72 | 0 |
| 116 | 1 |
| 65 | 0 |
Treinando um modelo de classificação binária
Para treinar o modelo, usaremos um algoritmo para ajustar os dados de treinamento a uma função que calcula a probabilidade de o rótulo da classe ser verdadeiro (em outras palavras, que o paciente tem diabetes). A probabilidade é medida como um valor entre 0,0 e 1,0, de tal forma que a probabilidade total para todas as classes possíveis é de 1,0. Assim, por exemplo, se a probabilidade de um paciente ter diabetes é de 0,7, então há uma probabilidade correspondente de 0,3 de que o paciente não é diabético.
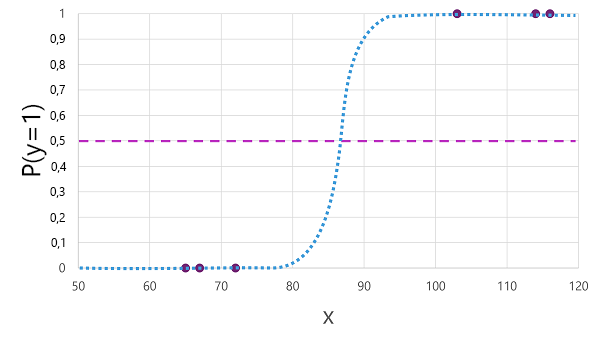
Existem muitos algoritmos que podem ser usados para classificação binária, como a regressão logística, que deriva uma função sigmoide (em forma de S) com valores entre 0,0 e 1,0, assim:
Nota
Apesar do nome, no aprendizado de máquina a regressão logística é usada para classificação, não para regressão. O ponto importante é a natureza logística da função que produz, que descreve uma curva em forma de S entre um valor inferior e superior (0,0 e 1,0 quando usado para classificação binária).
A função produzida pelo algoritmo descreve a probabilidade de y ser verdadeiro (y=1) para um dado valor de x. Matematicamente, você pode expressar a função assim:
f(x) = P(y=1 | x)
Para três das seis observações nos dados de treinamento, sabemos que y é definitivamente verdadeiro, então a probabilidade para essas observações de que y=1 é 1,0 e para as outras três, sabemos que y é definitivamente falsa, então a probabilidade de y=1 é 0,0. A curva em forma de S descreve a distribuição de probabilidade de modo que plotar um valor de x na linha identifique a probabilidade correspondente de que y é 1.
O diagrama também inclui uma linha horizontal para indicar o limiar no qual um modelo baseado nesta função irá prever verdadeiro (1) ou falso (0). O limiar situa-se no ponto médio para y (P(y) = 0,5). Para quaisquer valores neste ponto ou acima, o modelo irá prever verdadeiro (1), enquanto para quaisquer valores abaixo deste ponto irá prever falso (0). Por exemplo, para um paciente com um nível de glicose no sangue de 90, a função resultaria em um valor de probabilidade de 0,9. Uma vez que 0,9 é maior do que o limiar de 0,5, o modelo preveria verdadeiro (1) - em outras palavras, prevê-se que o paciente tenha diabetes.
Avaliação de um modelo de classificação binária
Assim como na regressão, ao treinar um modelo de classificação binária, você retém um subconjunto aleatório de dados com o qual validar o modelo treinado. Vamos supor que retivemos os seguintes dados para validar nosso classificador de diabetes:
| Glicose no sangue (x) | Diabético? y) |
|---|---|
| 66 | 0 |
| 107 | 1 |
| 112 | 1 |
| 71 | 0 |
| 87 | 1 |
| 89 | 1 |
A aplicação da função logística que derivamos anteriormente aos valores x resulta no gráfico a seguir.
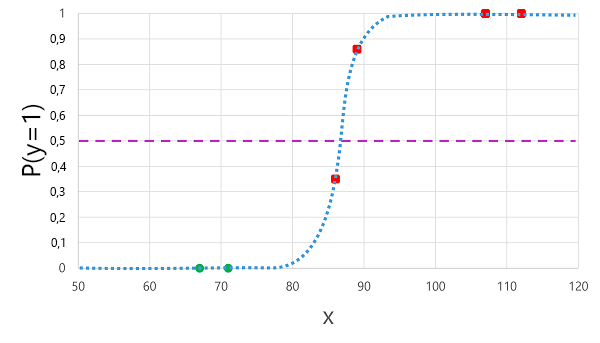
Com base no fato de a probabilidade calculada pela função estar acima ou abaixo do limiar, o modelo gera um rótulo previsto de 1 ou 0 para cada observação. Podemos então comparar os rótulos de classe previstos (ŷ) com os rótulos de classe reais (y), como mostrado aqui:
| Glicose no sangue (x) | Diagnóstico real de diabetes (y) | Diagnóstico previsto de diabetes (ŷ) |
|---|---|---|
| 66 | 0 | 0 |
| 107 | 1 | 1 |
| 112 | 1 | 1 |
| 71 | 0 | 0 |
| 87 | 1 | 0 |
| 89 | 1 | 1 |
Métricas de avaliação de classificação binária
O primeiro passo no cálculo de métricas de avaliação para um modelo de classificação binária é geralmente criar uma matriz do número de previsões corretas e incorretas para cada rótulo de classe possível:
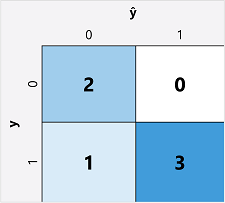
Essa visualização é chamada de matriz de confusão e mostra os totais de previsão onde:
- ŷ=0 e y=0: Verdadeiros negativos (TN)
- ŷ=1 e y=0: Falsos positivos (FP)
- ŷ=0 e y=1: Falsos negativos (FN)
- ŷ=1 e y=1: Verdadeiros positivos (TP)
A disposição da matriz de confusão é tal que as previsões corretas (verdadeiras) são mostradas em uma linha diagonal de cima-esquerda para baixo-direita. Muitas vezes, a intensidade da cor é usada para indicar o número de previsões em cada célula, então uma rápida olhada em um modelo que prevê bem deve revelar uma tendência diagonal profundamente sombreada.
Precisão
A métrica mais simples que você pode calcular a partir da matriz de confusão é a precisão - a proporção de previsões que o modelo acertou. A precisão é calculada como:
(TN+TP) ÷ (TN+FN+FP+TP)
No caso do nosso exemplo de diabetes, o cálculo é:
(2+3) ÷ (2+1+0+3)
= 5 ÷ 6
= 0.83
Assim, para os nossos dados de validação, o modelo de classificação da diabetes produziu previsões corretas 83% das vezes.
A precisão pode inicialmente parecer uma boa métrica para avaliar um modelo, mas considere isso. Suponhamos que 11% da população tem diabetes. Você poderia criar um modelo que sempre prevê 0, e ele alcançaria uma precisão de 89%, mesmo que não faça nenhuma tentativa real de diferenciar os pacientes avaliando suas características. O que realmente precisamos é de uma compreensão mais profunda de como o modelo se comporta na previsão de 1 para casos positivos e 0 para casos negativos.
Recuperar
Recall é uma métrica que mede a proporção de casos positivos que o modelo identificou corretamente. Em outras palavras, em comparação com o número de pacientes que têm diabetes, quantos o modelo previu ter diabetes?
A fórmula para o recall é:
TP ÷ (TP+FN)
Para o nosso exemplo de diabetes:
3 ÷ (3+1)
= 3 ÷ 4
= 0.75
Então, nosso modelo identificou corretamente 75% dos pacientes que têm diabetes como tendo diabetes.
Precisão
A precisão é uma métrica semelhante à recordação, mas mede a proporção de casos positivos previstos em que o rótulo verdadeiro é realmente positivo. Em outras palavras, que proporção dos pacientes previstos pelo modelo para ter diabetes realmente têm diabetes?
A fórmula para a precisão é:
TP ÷ (TP+FP)
Para o nosso exemplo de diabetes:
3 ÷ (3+0)
= 3 ÷ 3
= 1.0
Então, 100% dos pacientes previstos pelo nosso modelo para ter diabetes de fato têm diabetes.
Pontuação F1
A pontuação F1 é uma métrica geral que combina recall e precisão. A fórmula para a pontuação F1 é:
(2 x Precisão x Recall) ÷ (Precisão + Recall)
Para o nosso exemplo de diabetes:
(2 x 1,0 x 0,75) ÷ (1,0 + 0,75)
= 1,5 ÷ 1,75
= 0,86
Área sob a curva (AUC)
Outro nome para recall é a taxa de positivo verdadeiro (TPR), e há uma métrica equivalente chamada taxa de falso positivo (FPR) que é calculada como FP÷(FP+TN). Já sabemos que o TPR para o nosso modelo ao usar um limiar de 0,5 é 0,75, e podemos usar a fórmula para FPR para calcular um valor de 0÷2 = 0.
É claro que, se fôssemos alterar o limiar acima do qual o modelo prevê a verdade (1), isso afetaria o número de previsões positivas e negativas e, portanto, mudaria as métricas TPR e FPR. Essas métricas são frequentemente usadas para avaliar um modelo plotando uma curva ROC (característica do operador recebido) que compara o TPR e o FPR para cada valor limite possível entre 0,0 e 1,0:
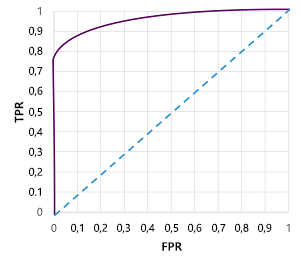
A curva ROC para um modelo perfeito iria direto até o eixo TPR à esquerda e, em seguida, através do eixo FPR no topo. Como a área do gráfico para a curva mede 1x1, a área sob esta curva perfeita seria 1.0 (o que significa que o modelo está correto 100% do tempo). Em contraste, uma linha diagonal da parte inferior esquerda para a parte superior direita representa os resultados que seriam alcançados adivinhando aleatoriamente um rótulo binário; produzindo uma área sob a curva de 0,5. Em outras palavras, dados dois rótulos de classe possíveis, você poderia razoavelmente esperar adivinhar corretamente 50% do tempo.
No caso do nosso modelo de diabetes, a curva acima é produzida, e a métrica de área sob a curva (AUC) é de 0,875. Uma vez que a AUC é superior a 0,5, podemos concluir que o modelo tem um melhor desempenho em prever se um paciente tem ou não diabetes do que adivinhar aleatoriamente.