Exercício - Crie emaranhamento quântico com Q#

7 minutos

Na unidade anterior, você aprendeu sobre o conceito de emaranhamento quântico e estados de Bell.

Agora, vamos criar emaranhamento quântico usando Q# e o Azure Quantum Development Kit. Para criar emaranhamento, você precisa aplicar duas operações quânticas: o portão Hadamard e o portão Controlled-NOT (CNOT).

A operação Controlled-NOT (CNOT)

Quando dois qubits estão entrelaçados, o estado de um qubit depende do estado do outro qubit. Portanto, para entrelaçar dois qubits você precisa de uma operação que atue em ambos os qubits ao mesmo tempo. Isso é chamado de operação multiqubit.

Para criar emaranhamento quântico, você precisa da operação multiqubit CNOT , que significa Controlled-NOT. Esta operação usa dois qubits como entrada, um atua como qubit de controle e o outro é o target qubit. A CNOT operação inverte o estado do segundo qubit (o target qubit) se, e somente se, o estado do primeiro qubit (o qubit de controle) for $|1\rangle$.

Entrada	Saída
$\ket{00}$	$\ket{00}$
$\ket{01}$	$\ket{01}$
$\ket{10}$	$\ket{11}$
$\ket{11}$	$\ket{10}$

No Q#, a CNOT operação atua em uma matriz de dois qubits, e inverte o segundo qubit se o primeiro qubit for One.

Emaranhamento com uma operação CNOT

Ao aplicar a operação Hadamard, H, e a operação Controlled-NOT, CNOT, você pode transformar dois qubits no estado $|00\rangle$ para o estado $\ket{\phiBell ^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$.

Eis como funciona:

Pegue dois qubits no estado $|00\rangle$. O primeiro qubit é o qubit de controle e o segundo qubit é o target qubit.
Crie um estado de superposição somente no qubit de controle aplicando $H$.

$$H |0_c\rangle={2}}\frac{1}{\sqrt{(|0_c\rangle+|1_c)\rangle$$

Gorjeta

Os subscritos ${}_c$ e ${}_t$ especificar o controle e target os qubits.
Aplique o $operador CNOT$ ao qubit de controle, que está em um estado de superposição, e ao target qubit, que está no estado $|0_t\rangle$.

$$CNOT \frac{1}{\sqrt{2}}(\ket{0_c}+\ket{1_c})\ket{0}_t = CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t}+|\ket{1_c 0_t}){1}{\sqrt$$=\frac{=$$2}(CNOT \ket{0_c 0_t} + CNOT \ket{1_c 0_t})$$\frac{1}{\sqrt$$==2}(\ket{0_c 0_t}+\ket{1_c 1_t)}$$

Criar um novo Q# ficheiro

Abra o Visual Studio Code.
Selecione Arquivo > Novo Arquivo de Texto e salve-o como Main.qs.
Selecione Exibir -> Paleta de Comandos e digiteQ#: Defina o perfil QIR target do Azure Quantum. Prima Enter.
Selecione Q#: Sem restrições.

Criar o estado $\ket{\phiBell ^+}$

Vamos começar criando o estado $\ket{\phiBell ^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$.

Primeiro, você precisa importar o Microsoft.Quantum.Diagnostics namespace da biblioteca Padrão, que contém a DumpMachine função. Esta função mostra o estado atual dos qubits. Copie e cole o código a seguir Q# no arquivo Main.qs .
```
import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
```
Gorjeta

Você também pode importar a biblioteca Standard substituindo Microsoft.Quantum por Std. Por exemplo, import Std.Diagnostics.* é equivalente a import Microsoft.Quantum.Diagnostics.*.

Crie a Main operação que retorna dois Result valores de tipo, que são os resultados de medição dos qubits.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    // Your code goes here
}

Dentro da operação, você aloca Main dois qubits, q1 e q2, que serão entrelaçados.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());
}

Aplique o portão de Hadamard, H, ao primeiro qubit, q1para colocá-lo em um estado de superposição. Em seguida, emaranhar os dois qubits usando a CNOT operação.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);
}

Use a DumpMachine função para exibir o estado atual dos qubits. Isso não é o mesmo que medir os qubits.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);

    DumpMachine();
}

Meça os qubits usando a M operação e armazene os resultados em m1 e m2. Em seguida, use a Reset operação para redefinir os qubits. No Q#, você sempre deve redefinir os qubits para o $|estado 0\rangle$ .

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {

    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);
    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

}

Finalmente, retorne os resultados da medição dos qubits com a return instrução. Seu arquivo Main.qs deve ter esta aparência:

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);

    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

    return (m1, m2);
}

Para executar o programa no simulador integrado, clique em Executar acima da Main operação ou pressione Ctrl+F5. Sua saída aparecerá no console de depuração.
Os resultados da medição são correlacionados, portanto, no final do programa, você obtém um resultado de (Zero, Zero) ou (One, One) com igual probabilidade.
Você pode visualizar o diagrama do circuito clicando em Circuito na lista de comandos acima da Main operação. O diagrama de circuito mostra o portão de Hadamard aplicado ao primeiro qubit e o portão CNOT aplicado a ambos os qubits.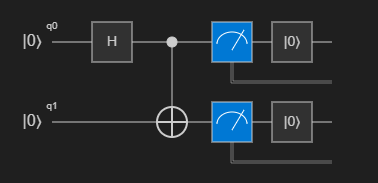

Criar outros estados Bell

Para criar outros estados Bell, você precisa aplicar operações Pauli $X$ e $Z$ adicionais aos qubits.

Por exemplo, para criar o estado $\ket{\phiBell ^-}=\frac1{\sqrt2}(|00-11|\rangle\rangle)$, você pode aplicar a operação Pauli $Z$ ao qubit de controle depois de aplicar o portão Hadamard. A $operação Z$ inverte o estado $\ket{+}$ para $\ket{-}$.

Gorjeta

Os estados $\frac{{1}{\sqrt{2}}(|0\rangle+|1\rangle)$ e $\frac{1}{\sqrt{{2}}(|0\rangle -|1\rangle)$ também são conhecidos como $\ket{+}$ e $\ket{{-}$, respectivamente.

Eis como funciona:

Pegue dois qubits no estado $|00\rangle$.
Crie um estado de superposição somente no qubit de controle aplicando $H$.

$$H |0_c\frac{\rangle={1}{\sqrt{2}}(|0_c\rangle+|1_c\rangle) =\ket{+_c}$$
Aplique a $operação Z$ ao qubit de controle.

$$Z \frac{{1}{\sqrt{{2}}(|0_c\rangle+|1_c\rangle)={2}}\frac{1}{\sqrt{(|0_c-1_c|\rangle\rangle)_c=\ket{{-}$$
Aplique o $operador CNOT$ ao qubit de controle e ao target qubit, que está no estado $|0_t\rangle$.

$$CNOT \frac{1}{\sqrt{2}}(\ket{0_c-1_c}}\ket{)\ket{0}_t = CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t-1_c 0_t|\ket{}})=$${1}{\sqrt$$=\frac{2}(CNOT \ket{0_c 0_t} - CNOT \ket{1_c 0_t})$$\frac{1}{\sqrt=$$=2}(\ket{0_c 0_t-1_c 1_t)\ket{}}$$

Da mesma forma, os estados $\ket{\pside Bell ^+}$ e $\ket{\psi^-}$ podem ser criados aplicando as operações Pauli $X$ e $Z$ aos qubits.

O estado $\ket{\pside Bell ^+}=\frac1{\sqrt2}(|01\rangle+|10\rangle)$ pode ser criado aplicando a operação Pauli $X$ ao target qubit depois de aplicar o portão de Hadamard.
O estado $\ket{\pside Bell ^-}=\frac1{\sqrt2}(|01-10\rangle|\rangle)$ pode ser criado aplicando o Pauli $Z$ ao qubit de controle e o Pauli $X$ ao target qubit depois de aplicar o portão de Hadamard.

Criar o estado $\ket{\phiBell ^-}$ em Q#

Modifique o Q# código para criar o estado $\ket{\phiBell ^-}$. Seu arquivo Main.qs deve ter esta aparência:

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    Z(q1); // Apply the Pauli Z operation to the control qubit
    CNOT(q1, q2);

    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

    return (m1, m2);
}

Para executar o programa no simulador integrado, clique em Executar acima da Main operação ou pressione Ctrl+F5. Sua saída aparecerá no console de depuração.
Você pode visualizar o diagrama do circuito clicando em Circuito na lista de comandos acima da Main operação. O diagrama de circuito mostra o portão de Hadamard aplicado ao primeiro qubit, o portão Pauli $Z$ aplicado ao primeiro qubit e o portão CNOT aplicado a ambos os qubits.

Na próxima unidade, você aprenderá a usar o emaranhamento para teletransportar informações quânticas.