O que é emaranhamento?
O entrelaçamento é uma das principais características da mecânica quântica que a distingue da mecânica clássica. Mas o que é emaranhamento? Como é que isto funciona? E por que é tão importante para a informação quântica?
Nesta unidade, você verá como definir e descrever o emaranhamento quântico e entender por que ele é um recurso tão poderoso para a computação quântica.
Compreender o emaranhamento quântico
Imagine que você tem dois qubits, $A$ e $B$. Os qubits são independentes uns dos outros, o que significa que a informação sobre o estado do qubit $A$, seja ele qual for, pertence apenas ao qubit $A$. Da mesma forma, as informações sobre o estado do qubit $B$ pertencem ao qubit $B$. Você pode descrever o estado de cada qubit. Neste caso, os qubits não estão entrelaçados, porque eles não estão compartilhando nenhuma informação.
Agora imagine que você enreda os qubits (você aprenderá como fazer isso mais tarde). Se os qubits A e B estão entrelaçados, então as informações sobre o estado do qubit $A$ não são independentes do estado do qubit $B$.$$$$ Quando entrelaçadas, as informações são compartilhadas entre ambos os qubits, e não há como inferir o estado do qubit $A$ ou o estado do qubit $B$. Você só pode descrever o estado do sistema global, não o estado dos qubits individuais.
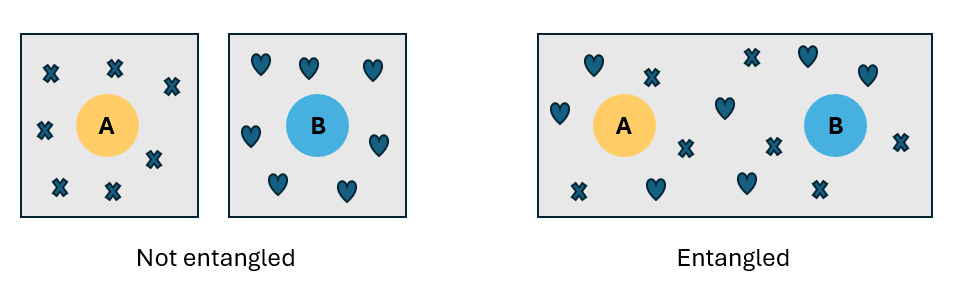
O emaranhamento é uma correlação quântica entre duas ou mais partículas. Se duas partículas estão entrelaçadas, elas não podem ser descritas independentemente, mas apenas como um sistema inteiro.
Descrevendo o emaranhamento quântico
Imagine dois qubits $A$ e $B$ tais que o estado do sistema $\ket{\phi}$ global é:
$$\ket{\phi}=\frac {\sqrt1 2}(\ket{0_A 0_B}+ \ket{1_A 1_B})$$
Nota
Na notação Dirac, $\ket{0_A 0_B}=|0\rangle_\text{A}|0\rangle_\text{B}$. A primeira posição corresponde ao primeiro qubit, e a segunda posição corresponde ao segundo qubit.
O sistema global $\ket{\phi}$ está numa superposição dos estados $\ket{{00}$ e $\ket{{11}$. Se você medir ambos os qubits, apenas dois resultados são possíveis: $\ket{{00}$ e $\ket{{11}$, e cada um tem a mesma probabilidade de $\frac{1}{{2}$.
Mas qual é o estado individual do qubit $A$? E do qubit $B$? Se você tentar descrever o estado do qubit $A$ sem considerar o estado do qubit $B$, você falharia. Os subsistemas $A$ e $B$ estão entrelaçados, o que significa que estão correlacionados e não podem ser descritos de forma independente.
Gorjeta
Se você está familiarizado com álgebra e notação de Dirac, um bom exercício é tentar modificar o $\ket{\phi}$ estado para obter algo como o estado de qubit $A$ vezes o estado de qubit $B$. Você verá que é impossível fazê-lo.
O estado $\ket{\phi}$ quântico é um estado especial emaranhado, chamado estado de Bell. Existem quatro estados Bell.
$$\ket{\phi^{+}}=\frac1{\sqrt2}\ket{{00} + \frac1{\sqrt2}\ket{{11}$$$$\ket{\phi^{-}}=\frac1{\sqrt2}\ket{00} - \frac1{\sqrt2}\ket{11}$$$$\ket{\psi^{+}}=\frac1{\sqrt2}\ket{{01} + \frac1{\sqrt2}\ket{{10}$$$$\ket{\psi^{-}}=\frac1{\sqrt2}\ket{01} - \frac1 2{\sqrt}\ket{10}$$
Usando o emaranhamento como um recurso
Neste ponto, você pode estar se perguntando: qual é o grande problema do emaranhamento?
Quando duas partículas estão entrelaçadas, os subsistemas são correlacionados e não podem ser descritos independentemente. Mas aqui está a parte interessante: os resultados da medição também estão correlacionados. Ou seja, qualquer operação que aconteça com o estado de um qubit em um par emaranhado, também afeta o estado do outro qubit.
Por exemplo, considere o $\ket{\phiestado ^{+}}$ ,
$$\ket{\phi^{+}}=\frac1{\sqrt2}\ket{{00} + \frac1{\sqrt2}\ket{{11}$$
Se você medir ambos os qubits, obterá $\ket{00}$ ou $\ket{11}$ com igual probabilidade. Há zero probabilidade de obter os estados $\ket{01}$ e $\ket{10}$.
Mas o que acontece se você medir apenas um qubit?
Se você medir apenas o qubit $A$ e obtiver o estado $\ket{0}$, isso significa que o sistema global entra em colapso para o estado $\ket{00}$. Este é o único resultado possível, uma vez que a probabilidade de medir $\ket{01}$ é zero.
Portanto, sem medir o qubit $B$ você pode ter certeza de que o segundo qubit também está em $\ket{0}$ estado. Os resultados da medição são correlacionados porque os qubits estão entrelaçados.
O emaranhamento pode existir entre duas partículas, mesmo que estejam separadas por grandes distâncias. Essa correlação é mais forte do que qualquer correlação clássica, e é um recurso chave para tarefas de processamento de informações quânticas, como teletransporte quântico, criptografia quântica e computação quântica.
Na próxima unidade, você escreverá um programa de Q# que cria estados de Bell aplicando operações quânticas a qubits.