Compreender a distribuição de dados
Compreender a distribuição dos seus dados é essencial para uma análise, visualização e construção de modelos de dados eficazes.
Se um conjunto de dados tem uma distribuição enviesada, isso significa que os pontos de dados não estão distribuídos uniformemente e tendem a inclinar-se mais para a direita ou para a esquerda. Isso pode levar a que um modelo preveja incorretamente pontos de dados de grupos sub-representados ou seja otimizado com base em uma métrica inadequada.
A importância da distribuição de dados
A seguir estão as principais áreas em que entender a distribuição de seus dados pode melhorar a precisão de seus modelos de aprendizado de máquina.
| Passo | Description |
|---|---|
| Análise exploratória de dados (EDA) | Compreender a distribuição dos dados facilita a exploração de um novo conjunto de dados e a localização de padrões. |
| Pré-processamento de dados | Algumas técnicas de pré-processamento, como normalização ou padronização, são usadas para tornar os dados mais normalmente distribuídos, o que é uma suposição comum em muitos modelos. |
| Seleção do modelo | Modelos diferentes fazem suposições diferentes sobre a distribuição dos dados. Por exemplo, alguns modelos assumem que os dados são normalmente distribuídos e podem não ter um bom desempenho se essa suposição for violada. |
| Melhorar o desempenho do modelo | Transformar sua variável de destino para reduzir a assimetria pode linearizar seu alvo, o que é útil para muitos modelos. Isso pode reduzir o alcance do seu erro e potencialmente melhorar o desempenho do seu modelo. |
| Relevância do modelo | Depois que um modelo é implantado na produção, é importante que ele permaneça relevante no contexto dos dados mais recentes. Se houver uma distorção de dados, ou seja, a distribuição de dados muda na produção em relação ao que foi usado durante o treinamento, o modelo pode sair do contexto. |
Compreender a distribuição de dados pode melhorar seu processo de criação de modelos. Ele permite que você estabeleça suposições mais precisas, identificando a média, o spread e o alcance de uma variável aleatória em seus recursos e alvo.
Vamos explorar alguns dos tipos de distribuição de dados mais comuns, como distribuições normais, binômias e uniformes.
Distribuição normal
Uma distribuição normal é representada por dois parâmetros: a média e o desvio padrão. A média indica onde a curva do sino está centralizada e o desvio padrão indica a dispersão da distribuição.
Vamos ver um exemplo de um recurso distribuído normal. O código abaixo gera os dados para o var recurso para fins de demonstração.
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
# Set the mean and standard deviation
mu, sigma = 0, 0.1
# Generate a normally distributed variable
var = np.random.normal(mu, sigma, 1000)
# Create a histogram of the variable using seaborn's histplot
sns.histplot(var, bins=30, kde=True)
# Add title and labels
plt.title('Histogram of Normally Distributed Variable')
plt.xlabel('Value')
plt.ylabel('Frequency')
# Show the plot
plt.show()
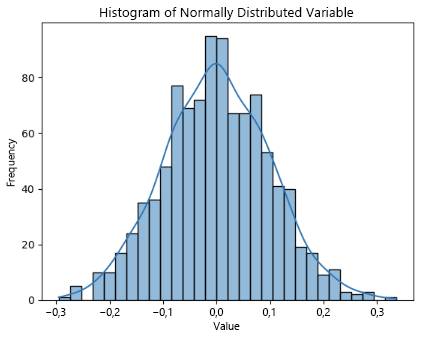
Observe que o var recurso é normalmente distribuído, onde a média e a mediana (percentil 50%) devem ser mais ou menos iguais. Para distribuições enviesadas, a média tende a inclinar-se para a cauda mais pesada.
No entanto, estas são verificações heurísticas e a determinação real é feita usando testes estatísticos específicos como o teste de Shapiro-Wilk ou o teste de Kolmogorov-Smirnov para normalidade.
Distribuição binomial
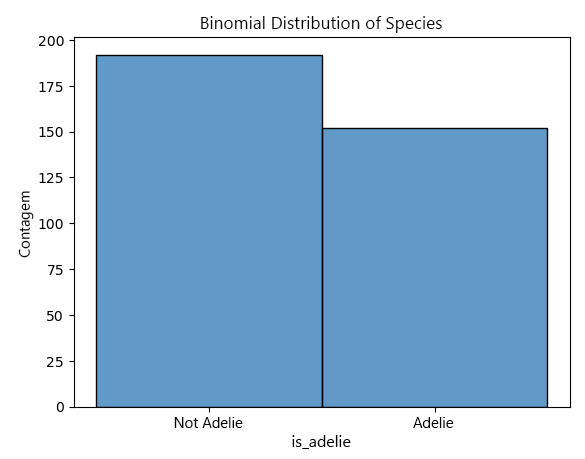
Suponha que você queira entender o quão bem uma determinada característica está sendo observada em um grupo de pinguins.
Você decide examinar um conjunto de dados de 200 pinguins para ver se eles são da espécie Adélia. Este é um problema de distribuição binomial porque há dois resultados possíveis (Adélie ou não Adelie), um número fixo de ensaios (200 pinguins), e cada ensaio é independente dos outros.
Depois de analisar o conjunto de dados, você descobre que 150 pinguins são da espécie Adélia.
Saber que seus dados seguem uma distribuição binomial permite que você faça previsões sobre conjuntos de dados futuros ou grupos de pinguins. Por exemplo, se você estudar outro grupo de 200 pinguins, você pode esperar que cerca de 150 sejam da espécie Adélia.
O código Python a seguir plota um histograma da is_adelie variável binomial. O discrete=True argumento em sns.histplot garante que os compartimentos sejam tratados como intervalos discretos. Isso significa que cada barra no histograma corresponde exatamente a uma categoria ou valor booleano, tornando o gráfico mais fácil de interpretar.
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
# Load the Penguins dataset from seaborn
penguins = sns.load_dataset('penguins')
# Create a binomial variable for 'species'
penguins['is_adelie'] = np.where(penguins['species'] == 'Adelie', 1, 0)
# Plot the distribution of 'is_adelie'
sns.histplot(data=penguins, x='is_adelie', bins=2, discrete=True)
plt.title('Binomial Distribution of Species')
plt.xticks([0, 1], ['Not Adelie', 'Adelie'])
plt.show()
Distribuição uniforme
Uma distribuição uniforme, também conhecida como distribuição retangular, é um tipo de distribuição de probabilidade na qual todos os resultados são igualmente prováveis. Cada intervalo do mesmo comprimento no suporte da distribuição tem a mesma probabilidade.
import numpy as np
import matplotlib.pyplot as plt
# Generate a uniform distribution
uniform_data = np.random.uniform(-1, 1, 1000)
# Plot the distribution
plt.hist(uniform_data, bins=20, density=True)
plt.title('Uniform Distribution')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()
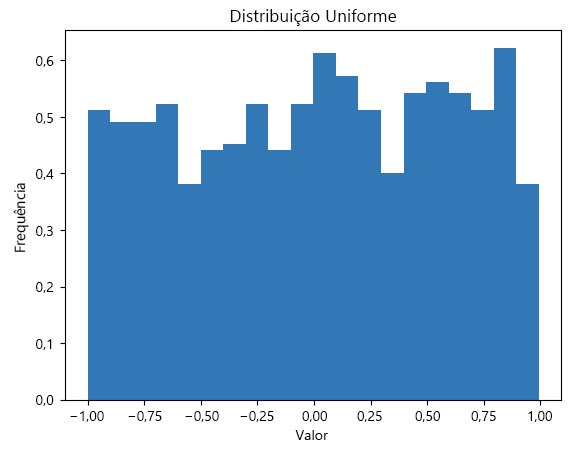
Neste código, a np.random.uniform função gera 1000 números aleatórios que são uniformemente distribuídos entre -1 e 1. O bins=30 argumento especifica que os dados devem ser divididos em 30 compartimentos e density=True garante que o histograma seja normalizado para formar uma densidade de probabilidade. Isso significa que a área sob o histograma se integra a 1, o que é útil ao comparar distribuições.
Nota
Você provavelmente obterá resultados diferentes se executar o código várias vezes. A ideia básica da aleatoriedade é que ela é imprevisível, e cada vez que você amostra, você pode obter resultados diferentes.
Você pode controlar esse processo definindo um valor de semente com np.random.seed. Isso é muito útil para testar e depurar na fase de construção do modelo, pois permite reproduzir os mesmos resultados.