Polilinhas e equações paramétricas
Use SkiaSharp para renderizar qualquer linha que você possa definir com equações paramétricas
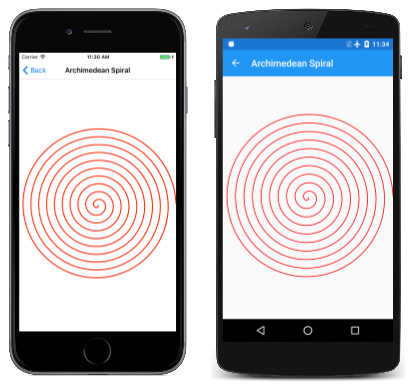
Na seção SkiaSharp Curves and Paths deste guia, você verá os vários métodos que SKPath definem para renderizar determinados tipos de curvas. No entanto, às vezes é necessário desenhar um tipo de curva que não é diretamente suportada pelo SKPath. Nesse caso, você pode usar uma polilinha (uma coleção de linhas conectadas) para desenhar qualquer curva que você possa definir matematicamente. Se você tornar as linhas pequenas o suficiente e numerosas o suficiente, o resultado parecerá uma curva. Esta espiral é, na verdade, 3.600 pequenas linhas:

Geralmente é melhor definir uma curva em termos de um par de equações paramétricas. Estas são equações para coordenadas X e Y que dependem de uma terceira variável, às vezes chamada t de tempo. Por exemplo, as seguintes equações paramétricas definem um círculo com um raio de 1 centrado no ponto (0, 0) para t de 0 a 1:
x = cos(2πt)
y = sin(2πt)
Se você quiser um raio maior que 1, você pode simplesmente multiplicar os valores de seno e cosseno por esse raio e, se precisar mover o centro para outro local, adicione esses valores:
x = xCenter + radius·cos(2πt)
y = yCenter + radius·sin(2πt)
Para uma elipse com os eixos paralelos ao horizontal e vertical, dois raios estão envolvidos:
x = xCenter + xRadius·cos(2πt)
y = yCenter + yRadius·sin(2πt)
Em seguida, você pode colocar o código SkiaSharp equivalente em um loop que calcula os vários pontos e os adiciona a um caminho. O código SkiaSharp a seguir cria um SKPath objeto para uma elipse que preenche a superfície de exibição. O loop percorre os 360 graus diretamente. O centro é metade da largura e altura da superfície do monitor, assim como os dois raios:
SKPath path = new SKPath();
for (float angle = 0; angle < 360; angle += 1)
{
double radians = Math.PI * angle / 180;
float x = info.Width / 2 + (info.Width / 2) * (float)Math.Cos(radians);
float y = info.Height / 2 + (info.Height / 2) * (float)Math.Sin(radians);
if (angle == 0)
{
path.MoveTo(x, y);
}
else
{
path.LineTo(x, y);
}
}
path.Close();
Isso resulta em uma elipse definida por 360 pequenas linhas. Quando é renderizado, ele parece suave.
Claro, você não precisa criar uma elipse usando uma polilinha porque SKPath inclui um AddOval método que faz isso para você. Mas talvez você queira desenhar um objeto visual que não é fornecido pelo SKPath.
A página Espiral de Arquimedes tem código semelhante ao código de elipse, mas com uma diferença crucial. Ele dá uma volta em torno dos 360 graus do círculo 10 vezes, ajustando continuamente o raio:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
SKPoint center = new SKPoint(info.Width / 2, info.Height / 2);
float radius = Math.Min(center.X, center.Y);
using (SKPath path = new SKPath())
{
for (float angle = 0; angle < 3600; angle += 1)
{
float scaledRadius = radius * angle / 3600;
double radians = Math.PI * angle / 180;
float x = center.X + scaledRadius * (float)Math.Cos(radians);
float y = center.Y + scaledRadius * (float)Math.Sin(radians);
SKPoint point = new SKPoint(x, y);
if (angle == 0)
{
path.MoveTo(point);
}
else
{
path.LineTo(point);
}
}
SKPaint paint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Red,
StrokeWidth = 5
};
canvas.DrawPath(path, paint);
}
}
O resultado também é chamado de espiral aritmética porque o deslocamento entre cada loop é constante:
Observe que o SKPath é criado em um using bloco. Isso SKPath consome mais memória do que os objetos nos programas anteriores, o SKPath que sugere que um using bloco é mais apropriado para descartar quaisquer recursos não gerenciados.