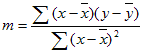Método WorksheetFunction.LinEst (Excel)
Calcula as estatísticas de uma linha usando o método menos quadrados para calcular uma linha reta que melhor se encaixa em seus dados e retorna uma matriz que descreve a linha. Como essa função retorna uma matriz de valores, ela deve ser inserida como uma fórmula matricial.
Sintaxe
expressão. LinEst (Arg1, Arg2, Arg3, Arg4)
Expressão Uma variável que representa um objeto WorksheetFunction .
Parâmetros
| Nome | Obrigatório/Opcional | Tipo de dados | Descrição |
|---|---|---|---|
| Arg1 | Obrigatório | Variantes | Known_y é - o conjunto de valores y que você já conhece na relação y = mx + b. |
| Arg2 | Opcional | Variantes | Val_conhecidos_x - um conjunto opcional de valores x que talvez você já conheça na relação y = mx + b. |
| Arg3 | Opcional | Variantes | Constante - um valor lógico que especifica a necessidade de forçar ou não a constante b igual a zero. |
| Arg4 | Opcional | Variantes | Estatísticas - um valor lógico especificando a necessidade de retornar ou não estatísticas adicionais de regressão. |
Valor de retorno
Variant
Comentários
A equação da linha é y = mx + b ou y = m1x1 + m2x2 + ... + b (se houver vários intervalos de valores x), em que o valor y dependente é uma função dos valores x independentes. Os valores m são coeficientes correspondentes a cada valor x e b é um valor constante. Observe que y, x e m podem ser vetores. A matriz que o LinEst retorna é {mn,mn-1,...,m1,b}. O LinEst também pode retornar estatísticas de regressão adicionais.
Se a matriz known_y estiver em uma única coluna, cada coluna de known_x será interpretada como uma variável separada.
Se a matriz known_y estiver em uma única linha, cada linha de known_x será interpretada como uma variável separada.
A matriz val_conhecidos_x pode incluir um ou mais conjuntos de variáveis. Se apenas uma variável for usada, val_conhecidos_y e val_conhecidos_x podem ser intervalos de qualquer formato, desde que tenham dimensões iguais. Se mais de uma variável for usada, val_conhecidos_y deverá ser um vetor (ou seja, um intervalo com altura de uma linha ou largura de uma coluna).
Se known_x for omitido, presume-se que seja a matriz {1,2,3,...} do mesmo tamanho que a do known_y.
Se const for True ou omitido, b será calculado normalmente.
Se const for False, b será definido como 0 e os valores m serão ajustados para se ajustar
y = mx.Se as estatísticas forem True, o LinEst retornará as estatísticas de regressão adicionais, portanto, a matriz retornada será
{mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r2,sey;F,df;ssreg,ssresid}.Se as estatísticas forem False ou omitidas, o LinEst retornará apenas os m-coeficientes e a constante b.
Há exemplos de estatísticas adicionais de regressão a seguir.
| Estatística de regressão | Descrição |
|---|---|
| se1,se2,...,sen | Os valores padrão de erro dos coeficientes m1,m2,...,mn. |
| Seb | O valor de erro padrão para a constante b (seb = #N/A quando const é False). |
| R2 | O coeficiente de determinação. Compara valores y reais e estimados e intervalos no valor de 0 a 1. Se for 1, há uma correlação perfeita no exemplo — não há diferença entre o valor y estimado e o valor y real. Por outro lado, se o coeficiente de determinação for 0, a equação de regressão não ajudará a prever um valor y. |
| sey | O erro padrão da estimativa de y. |
| S | A estatística F ou valor F observado. Use a estatística F para determinar se a relação observada entre as variáveis dependentes e independentes ocorrerá aleatoriamente. |
| Df | Os graus de liberdade. Use os graus de liberdade para ajudá-lo a obter valores F críticos em uma tabela estatística. Compare os valores encontrados na tabela com a estatística F retornada pelo LinEst para determinar um nível de confiança para o modelo. |
| ssreg | A soma de regressão dos quadrados. |
| ssresid | A soma residual dos quadrados. |
A ilustração a seguir mostra a ordem na qual as estatísticas adicionais de regressão são retornadas.
Você pode descrever qualquer linha reta com a inclinação e a interceptação y: Slope (m). Para encontrar a inclinação de uma linha, geralmente escrita como m, leve dois pontos na linha , (x1,y1) e (x2,y2); a inclinação é igual a (y2 - y1)/(x2 - x1). Y-intercept (b): a interceptação y de uma linha, muitas vezes escrita como b, é o valor de y no ponto em que a linha cruza o eixo y. A equação de uma linha reta é y = mx + b. Depois de conhecer os valores de m e b, você pode calcular qualquer ponto na linha conectando o valor y ou x a essa equação. Também é possível usar a função TENDÊNCIA.
Quando você tem apenas uma variável x independente, você pode obter os valores de inclinação e interceptação y diretamente usando as seguintes fórmulas:
- Inclinação:
=INDEX(LINEST(known_y's,known_x's),1) - Interceptação Y:
=INDEX(LINEST(known_y's,known_x's),2)
A precisão da linha calculada pelo LinEst depende do grau de dispersão em seus dados. Quanto mais lineares os dados, mais preciso é o modelo LinEst . O LinEst usa o método de mínimos quadrados para determinar o melhor ajuste para os dados. Quando você tem apenas uma variável x independente, os cálculos para m e b são baseados nas seguintes fórmulas:
onde x e y são exemplos significa, ou seja, x = AVERAGE(conhecido x's) e y = AVERAGE(known_y's).
As funções de ajuste de linha e curva LinEst e LogEst podem calcular a melhor linha reta ou curva exponencial que se encaixa em seus dados. No entanto, você precisa escolher o resultado mais adequado aos seus dados. Você pode calcular TREND(known_y's,known_x's) para uma linha reta ou GROWTH(known_y's, known_x's) para uma curva exponencial. Essas funções, sem o argumento novos_valores_x, retornam uma matriz de valores y previstos ao longo dessa linha ou curva nos pontos de dados reais. Você poderá então comparar os valores previstos com os reais. Talvez seja conveniente colocá-los em um gráfico para comparação visual.
Na análise de regressão, o Microsoft Excel calcula para cada ponto a diferença quadrada entre o valor y estimado para esse ponto e seu valor y real. A soma dessas diferenças quadradas é chamada de soma residual de quadrados, ssresid. Em seguida, o Excel calcula a soma total de quadrados, sstotal. Quando const = TRUE ou omitido, a soma total de quadrados é a soma das diferenças quadradas entre os valores y reais e a média dos valores y. Quando const = FALSE, a soma total de quadrados é a soma dos quadrados dos valores y reais (sem subtrair o valor y médio de cada y-valor individual). Em seguida, a soma de regressão de quadrados, ssreg, pode ser encontrada a partir de ssreg = sstotal - ssresid. Quanto menor a soma residual de quadrados for, em comparação com a soma total de quadrados, maior o valor do coeficiente de determinação, r2, que é um indicador de quão bem a equação resultante da análise de regressão explica a relação entre as variáveis; r2 é igual a ssreg/sstotal.
Em alguns casos, uma ou mais colunas X (suponha que Y e X estão em colunas) pode não ter nenhum valor preditivo adicional na presença das outras colunas X. Em outras palavras, a eliminação de uma ou mais colunas X pode levar a valores Y previstos que são igualmente precisos. Nesse caso, essas colunas X redundantes devem ser omitidas do modelo de regressão. Esse fenômeno é chamado de collinearidade porque qualquer coluna X redundante pode ser expressa como uma soma de múltiplos das colunas X não redundantes. O LinEst verifica a collinearidade e remove todas as colunas X redundantes do modelo de regressão quando as identifica. As colunas X removidas podem ser reconhecidas na saída LinEst como tendo 0 coeficientes, bem como 0 se's.
- Se uma ou mais colunas forem removidas como redundantes, o DF será afetado porque o DF depende do número de colunas X realmente usadas para fins preditivos. Se o df for alterado porque as colunas X redundantes forem removidas, os valores de sey e F também serão afetados.
- A collinearidade deve ser relativamente rara na prática. No entanto, um caso em que é mais provável que ele surja é quando algumas colunas X contêm apenas 0 e 1 como indicadores de se um assunto em um experimento é ou não um membro de um determinado grupo. Se const = TRUE ou omitido, o LinEst inserirá efetivamente uma coluna X adicional de todas as 1 para modelar a interceptação. Se você tiver uma coluna com uma 1 para cada assunto, se for masculino ou 0, e também tiver uma coluna com uma 1 para cada assunto, se feminina, ou 0, se não for, esta última coluna será redundante, pois as entradas nela podem ser obtidas com a subtração da entrada na coluna indicador masculino da entrada na coluna adicional de todas as 1 adicionadas pelo LinEst.
- df é calculado da seguinte maneira quando nenhuma coluna X é removida do modelo devido à collinearidade: se houver k colunas de known_x e const = TRUE ou omitido,
df = n - k - 1. Se const = FALSE,df = n - k. Em ambos os casos, cada coluna X removida devido à colinearidade aumenta df em 1.
As fórmulas que fornecem matrizes devem ser inseridas como fórmulas matriciais.
- Ao inserir uma constante, como um argumento val_conhecidos_x, use vírgulas na mesma linha e ponto-e-vírgulas para separar linhas. Os caracteres separadores podem ser diferentes dependendo da configuração da localidade em Opções Regionais e de Idioma no Painel de Controle.
- Lembre-se de que os valores y previstos pela equação de regressão talvez não sejam válidos se estiverem fora do intervalo dos valores y usados para determinar a equação.
O algoritmo subjacente usado na função LinEst é diferente do algoritmo subjacente usado nas funções Slope e Intercept . A diferença entre esses algoritmos pode levar a diferentes resultados quando os dados forem indeterminados e colineares. Por exemplo, se os pontos de dados do argumento val_conhecidos_y forem 0 e os pontos de dados do argumento val_conhecidos_x forem 1:
- O LinEst retorna um valor de 0. O algoritmo LinEst foi projetado para retornar resultados razoáveis para dados collinear e, nesse caso, pelo menos uma resposta pode ser encontrada.
- Inclinar e Interceptar retornar um #DIV/0! . O algoritmo Slope e Intercept foi projetado para procurar uma e apenas uma resposta e, nesse caso, pode haver mais de uma resposta.
Suporte e comentários
Tem dúvidas ou quer enviar comentários sobre o VBA para Office ou sobre esta documentação? Confira Suporte e comentários sobre o VBA para Office a fim de obter orientação sobre as maneiras pelas quais você pode receber suporte e fornecer comentários.