Resultados de modelos de machine learning
Isto artigo discute matrizes de confusão, problemas de classificação e precisão em modelos de aprendizado de máquina (ML). O objetivo é melhorar a sua compreensão da precisão em resultados de predição de ML. A audiência de destino inclui engenheiros, analistas e gestores que pretendem criar conhecimentos e competências em ciência de dados.
Matriz de confusão
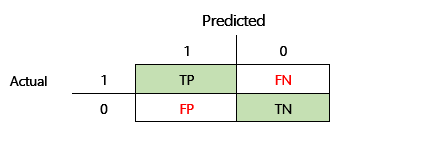
Depois de um problema de ML ser formado num conjunto de dados históricos, é testado utilizando dados que são retidos a partir do processo de formação. Dessa forma, pode comparar as predições do modelo formado com os valores reais. A matriz de confusão fornece um meio de avaliar o êxito de um problema de classificação e quando comete erros (ou seja, quando se torna "confuso").
Por exemplo, o seu objetivo é prever se um animal de estimação é um cão ou um gato, com base em alguns atributos físicos e comportamentais. Se tiver um conjunto de dados de teste que contém 30 cães e 20 gatos, a matriz de confusão pode ser semelhante à ilustração a seguir.
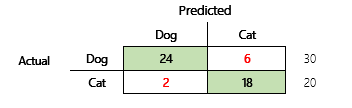
Os números nas células verdes representam as predições corretas. Como pode ver, o modelo previu corretamente uma percentagem maior dos gatos reais. A precisão geral do modelo é fácil de calcular. Neste caso, é 42 ÷ 50 ou 0,84.
Classificadores de várias classes numa matriz de confusão
A maioria das discussões sobre a matriz de confusão concentra-se em classificadores binários, como no exemplo anterior. Este é um caso especial em que outras métricas podem ser consideradas, como sensibilidade e revocação.
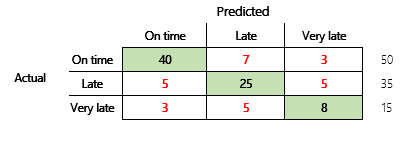
Em seguida, consideraremos um problema de classificação para um cenário de finanças que tem três estados. O modelo prevê se uma fatura de cliente será paga dentro do prazo, atrasada ou muito atrasada. Por exemplo, de 100 faturas teste, 50 são pagas dentro do prazo, 35 são pagas atrasadas e 15 são pagas muito atrasadas. Neste caso, um modelo pode produzir uma matriz de confusão que se assemelha à ilustração a seguir.
 ]
]
Uma matriz de confusão fornece mais informações do que uma métrica de precisão simples. No entanto, ainda é relativamente fácil de compreender. Uma matriz de confusão informa se tem um conjunto de dados equilibrado no qual as classes de saída têm contagens semelhantes. Para o cenário de várias classes, informa o quanto uma predição pode estar errada quando as classes de saída são ordinais, como no exemplo anterior sobre pagamentos de cliente.
Precisão do modelo
Diferentes métricas de precisão têm a vantagem de quantificar a qualidade do modelo.
Como a precisão é uma métrica fácil de compreender, é um bom ponto de partida para explicar um modelo a outras pessoas, especialmente para os utilizadores do modelo que não são cientistas de dados. Não é necessário compreender estatísticas para compreender a precisão do modelo. Quando houver uma matriz de confusão disponível, esta fornecerá mais informações sobre o desempenho do modelo.
No entanto, para ter uma compreensão mais abrangente, devem ser observados vários desafios associados à precisão. A utilidade da métrica depende do contexto do problema. Uma pergunta que muitas vezes surge em relação ao desempenho do modelo é: "Quão bom é o modelo?" No entanto, a resposta a esta pergunta não é necessariamente simples. Considere a seguinte matriz de confusão (modelo 2).
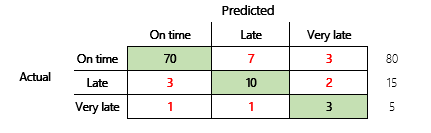
Um cálculo rápido mostra que a precisão deste modelo é (70 + 10 + 3) ÷ 100 ou 0,83. Na superfície, este resultado parece ser melhor do que o resultado do modelo de várias classes anterior (modelo 1), que tem uma precisão de 0,73. Mas é realmente melhor?
Para começar a discutir esta pergunta, considere a precisão de uma suposição ingénua. Para um problema de classificação, uma estimativa simples sempre prevê a classe mais comum. Para o modelo 1, essa estimativa será "dentro do prazo" e produzirá uma precisão de 0,50. A estimativa do modelo 2 também será "dentro do prazo" e produzirá uma precisão de 0,80. Como o modelo 1 melhora a suposição ingénua de 0,73 - 0,50 = 0,23, enquanto que o modelo 2 melhora a suposição ingénua de 0,83 – 0,80 = 0,03, o modelo 1 é melhor, mesmo que tenha uma precisão menor. O cálculo revela que a avaliação real da qualidade de um modelo requer mais contexto do que o valor de precisão.
É importante observar outro aspeto. Considere um cenário no qual um teste médico é utilizado para detetar uma doença num paciente. Este é um problema de classificação binária em que um resultado positivo indica que o paciente tem a doença. Neste cenário, deve pensar no impacto dos seguintes erros:
- Falsos positivos, em que o teste diz que um paciente tem a doença, mas o paciente não a tem realmente.
- Falsos negativos, em que o teste diz que um paciente não tem a doença, mas realmente tem.
Obviamente, os dois tipos de erro são indesejados, mas qual é pior? Mais uma vez, depende. No caso de uma doença que ameaça a vida e exige tratamento rápido, a minimização de falsos negativos (seguidos de testes adicionais, espera-se) é algo prioritário. Em outras situações menos críticas, os criadores de modelos podem minimizar falsos positivos. De qualquer forma, uma conclusão razoável é que para determinar efetivamente a qualidade de um modelo, deve ter mais informações do que as fornecidas por uma métrica de precisão.
Recomendações
A precisão é uma ferramenta importante para a comunicação com especialistas em domínio que não estão familiarizados com as estatísticas. No entanto, para que as informações sejam úteis, é fundamental que o contexto adicional seja fornecido juntamente com o valor de precisão.
Para o cenário de predição de pagamento, pode definir um destino para o modelo ML que inclui fatores em diferentes comportamentos de pagamento. O destino é que o modelo deve melhorar numa suposição ingénua reduzindo o número de respostas incorretas em pelo menos 50%. Por outras palavras, quer uma precisão de destino que divide a diferença entre a precisão de uma suposição ingénua e 100%.
A tabela a seguir resume esse princípio para as matrizes de confusão neste artigo.
| Modelo | Suposição ingénua | Destino | Precisão do modelo | O objetivo foi cumprido? |
|---|---|---|---|---|
| Modelo 1 | 0,50 | 0,75 | 0,73 | Quase. Este modelo melhora consideravelmente a suposição. |
| Modelo 2 | 0,80 | 0,90 | 0,83 | N.º É necessário melhorar. |
Precisão F1 da classificação
A consideração final neste artigo é uma medida mais avançada do desempenho de ML de classificação que é conhecida como precisão F1.
Para que a precisão F1 possa ser definida, duas métricas adicionais devem ser introduzidas: precisão e revocação. A precisão indica o número total de predições especificadas como positivas que são atribuídas corretamente. Esta métrica também é conhecida como valor de predição positivo. Revocação é o número total de casos positivos reais que foram previstos corretamente. Esta métrica também é conhecida como sensibilidade.
Na matriz de confusão da ilustração anterior, estas métricas são calculadas da seguinte maneira:
- Precisão = TP ÷ (TP + FP)
- Revocação = TP ÷ (TP + FN)
A medida F1 combina precisão e revocação. O resultado é a média harmónica dos dois valores. Ele é calculado da seguinte maneira:
- F1 = 2 × (precisão × revocação) ÷ (precisão + revocação)
Vejamos um exemplo concreto. No início deste artigo, havia um exemplo de um modelo que previa se um animal era um cão ou um gato. A ilustração é repetida aqui.
Estes serão os resultados se "cão" for utilizado como a resposta positiva.
- Precisão = 24 ÷ (24 + 2) = 0,9231
- Revocação = 24 ÷ (24 + 6) = 0,8
- F1 = 2 × (0,9231 × 0,8) ÷ (0,9231 + 0,8) = 0,8572
Como pode ver, o valor F1 encontra-se entre os valores de precisão e revocação.
Embora a precisão F1 não seja tão fácil de entender, adiciona nuances ao número de precisão básica. Também pode ajudar com conjuntos de dados não equilibrados, conforme mostra a seguinte discussão.
A secção Precisão do modelo deste artigo comparou as duas matrizes de confusão a seguir. Embora o primeiro modelo tenha a precisão menor, foi considerado um modelo mais útil, pois mostrou mais melhorias do que a suposição predefinida de um pagamento dentro do prazo.


Vamos ver como estes dois modelos se comparam quando é utilizada a pontuação F1. A pontuação F1 considera a precisão e a revocação de cada estado, e então o cálculo de macro F1 calcula a média da pontuação F1 em todos os estados para determinar uma pontuação F1 geral. Há outras variantes F1, mas o mais interessante é considerar a versão da macro, dada a mesma consideração que é dada a todos os três estados.
Para simplificar os cálculos, os conjuntos de amostras foram criados para coincidir com os valores reais e previstos. Estas matrizes utilizaram a biblioteca de métricas do sklearn no Python para calcular os valores. Este é o resultado.
| Modelo | Suposição ingénua | Precisão | Macro F1 |
|---|---|---|---|
| Modelo 1 | 0,5 | 0,73 | 0,67 |
| Modelo 2 | 0,80 | 0,83 | 0,66 |
Para obter mais detalhes sobre como este cálculo funciona, aqui está o relatório de classificação sklearn.metrics para o modelo 1. Os três estados, "Dentro do prazo", "Atrasado" e "Muito atrasado", são representados pelas linhas etiquetadas 1, 2 e 3, respetivamente. A média da macro é apenas a média da coluna "pontuação f1".
| precisão | revocação | pontuação f1 | |
|---|---|---|---|
| 1 | 0,83 | 0,80 | 0,82 |
| 2 | 0,68 | 0,71 | 0,69 |
| 3 | 0,50 | 0,50 | 0,50 |
Conforme mostram os resultados, os dois modelos têm uma pontuação de precisão da macro F1 quase idêntica. Neste e em muitos outros casos, a precisão F1 fornece um indicador melhor da capacidade de um modelo. Quanto à precisão, a interpretação dos resultados requer que compreenda o que é mais importante considerar no modelo.