Determinar a combinação ideal de descontos sobrepostos

Isto artigo descreve como determinar a combinação óptima de descontos sobrepostos em Microsoft Dynamics 365 Commerce.

Quando os descontos se sobrepõem, é necessário determinar a combinação de descontos sobrepostos que produzirá o total da transação mais baixo ou o desconto total mais elevado. Quando o montante do desconto varia de acordo com o preço dos produtos comprados, como é o caso do desconto de retalho comum "Compre um, leve outro com X por cento de desconto" (BOGO), isto processo torna-se um problema de otimização combinatória.

Isto artigo aplica-se a Microsoft Dynamics AX 2012 R3 com KB 3105973 (lançado a 2 de novembro de 2015) ou posterior, e a Dynamics 365 Commerce. Para determinar a combinação de descontos sobrepostos a aplicar atempadamente, introduzimos um método para aplicar descontos sobrepostos. Chamamos a isto novo método marginal value ranking. No método de classificação do valor marginal, é calculado um valor para cada desconto sobreposto, utilizando o valor do desconto nos produtos partilhados. Os descontos sobrepostos são então aplicados do valor relativo mais elevado para o valor relativo mais baixo. Para mais informações sobre o novo método, consulte a secção Método de classificação do valor marginal mais adiante neste artigo. A classificação do valor marginal não é utilizada quando os montantes de desconto de um produto não são afectados por outro produto na transação. Por exemplo, isto método não é utilizado para dois descontos simples, ou para um desconto simples e um desconto por quantidade de um único produto.

Exemplos de descontos

Pode criar um número ilimitado de descontos para um conjunto comum de produtos. No entanto, como não há limite, podem ocorrer problemas de desempenho quando se tenta calcular os descontos que devem ser utilizados nos vários produtos. Os exemplos seguintes ilustram esta questão de forma mais pormenorizada. No exemplo 1, começamos com dois produtos e dois descontos sobrepostos. Depois, no exemplo 2, mostramos como a questão evolui à medida que são adicionados mais produtos.

Exemplo 1: Dois produtos e dois descontos

Neste exemplo, são necessários dois produtos para se poder beneficiar de cada desconto e os descontos não podem ser combinados. Os descontos neste exemplo são Melhor preço descontos. Ambos os produtos podem beneficiar de ambos os descontos. Eis os dois descontos.

Para dois produtos quaisquer, o melhor destes dois descontos depende dos preços dos dois produtos. Quando o preço de ambos os produtos é igual ou quase igual, o desconto 1 é melhor. Quando o preço de um produto é significativamente inferior ao preço do outro produto, o desconto 2 é melhor. Eis a regra matemática para avaliar estes dois descontos um contra o outro.

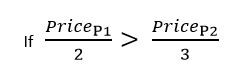
Nota

Quando o preço do produto 1 é igual a dois terços do preço do produto 2, os dois descontos são iguais. Neste exemplo, a percentagem de desconto efectiva para o desconto 1 varia entre alguns por cento (quando os preços dos dois produtos estão muito afastados) e um máximo de 25 por cento (quando os dois produtos têm o mesmo preço). A percentagem de desconto efectiva para o desconto 2 é fixa. É sempre 20 por cento. Como a percentagem de desconto efectiva para o desconto 1 tem um intervalo que pode ser superior ou inferior ao desconto 2, o melhor desconto depende dos preços dos dois produtos que devem ser descontados. Neste exemplo, o cálculo é concluído rapidamente, porque apenas dois descontos são aplicados a apenas dois produtos. Só há duas combinações possíveis: uma aplicação do desconto 1 ou uma aplicação do desconto 2. Não há permutações a calcular. O valor de cada desconto é calculado através da utilização de ambos os produtos, sendo utilizado o melhor desconto.

Exemplo 2: Quatro produtos e dois descontos

De seguida, vamos utilizar quatro produtos e os mesmos dois descontos. Os quatro produtos podem beneficiar de ambos os descontos. Existem 12 combinações possíveis. No final, serão aplicados dois descontos à transação numa de três combinações: duas aplicações do desconto 1, duas aplicações do desconto 2, ou uma aplicação do desconto 1 e uma aplicação do desconto 2. Para ilustrar as combinações possíveis, vamos analisar dois conjuntos diferentes de quatro produtos que têm preços diferentes:

• Os quatro produtos têm o mesmo preço, $15.00. Neste caso, a melhor combinação de desconto é duas aplicações do desconto 1. Dois produtos terão o preço total e dois terão um desconto de 50%. O total com desconto para a transação é $45 (15 + 15 + 7,50 + 7,50), que é $15 (25 por cento) do total sem desconto de $60. O desconto 2 é apenas $12 (20 por cento).
• Dois produtos são $20 cada, um produto é $15, e um produto é $5. Neste caso, a melhor combinação de descontos é uma aplicação do desconto 2 e uma aplicação do desconto 1. Os quadros seguintes ilustram os descontos.

Para ler os quadros, utilize um produto de uma linha e um produto de uma coluna. Por exemplo, na tabela do desconto 1, ao combinar os dois produtos $20, obtém $10 de desconto. Na tabela do desconto 2, quando combina o produto $15 com o produto $5, obtém um desconto de $4.

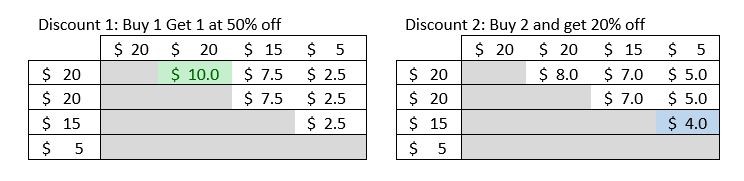
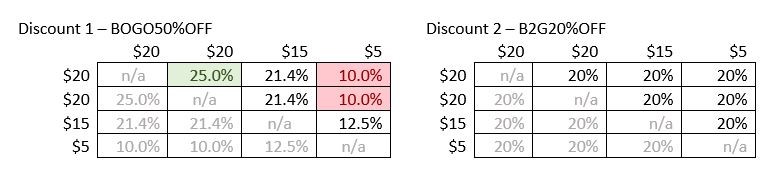
Em primeiro lugar, encontramos o maior desconto disponível em dois produtos quaisquer, utilizando qualquer um dos descontos. Os dois quadros mostram o montante do desconto para todas as combinações dos dois produtos. As partes sombreadas das tabelas representam casos em que um produto é emparelhado com ele próprio, o que não podemos fazer, ou um emparelhamento inverso de dois produtos que produz o mesmo montante de desconto e pode ser ignorado. Observando as tabelas, pode ver que o desconto 1 para os dois artigos do $20 é o maior desconto disponível para qualquer um dos descontos nos quatro produtos. (Isto desconto está assinalado a verde no primeiro quadro.) Restam apenas o produto $15 e o produto $5. Observando novamente os dois quadros, verifica-se que, para estes dois produtos, o desconto 1 dá um desconto de $2.50, enquanto o desconto 2 dá um desconto de $4. Por conseguinte, seleccionamos o desconto 2. O desconto total é de $14. Para tornar esta discussão mais fácil de visualizar, eis mais duas tabelas que mostram a percentagem de desconto efectiva para todas as combinações possíveis de dois produtos, tanto para o desconto 1 como para o desconto 2. Apenas metade da lista de combinações está incluída, porque, para estes dois descontos, a ordem pela qual os dois produtos são colocados no desconto não importa. O desconto efetivo mais elevado (25%) está destacado a verde e o desconto efetivo mais baixo (10%) está destacado a vermelho.

Nota

Quando os preços variam e dois ou mais descontos concorrem entre si, a única forma de garantir a melhor combinação de descontos é avaliar ambos os descontos e compará-los.

Total de combinações possíveis

Esta secção continua o exemplo da secção anterior. Vamos acrescentar mais produtos e outro desconto e ver quantas combinações têm de ser calculadas e comparadas. A tabela seguinte mostra o número de combinações de desconto possíveis à medida que a quantidade do produto aumenta. O quadro mostra o que acontece tanto quando há dois descontos sobrepostos, como no exemplo anterior, como quando há três descontos sobrepostos. O número de combinações de descontos possíveis que devem ser avaliadas excede rapidamente o que até um computador rápido pode calcular e comparar com rapidez suficiente para ser aceitável para transacções de retalho.

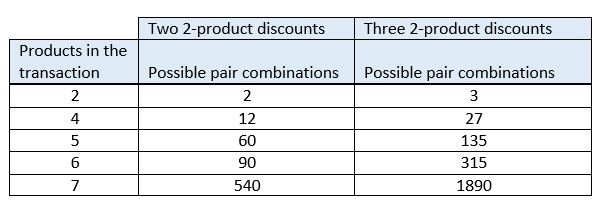
Quando são aplicadas quantidades ainda maiores ou mais descontos sobrepostos, o número total de combinações de descontos possíveis atinge rapidamente os milhões ou mesmo milhares de milhões, e o tempo necessário para avaliar e selecionar a melhor combinação possível torna-se rapidamente percetível. Foram feitas algumas optimizações no motor de preços para reduzir o número total de combinações que devem ser avaliadas. No entanto, como o número de descontos sobrepostos e as quantidades numa transação não são limitados, um grande número de combinações terá sempre de ser avaliado sempre que houver descontos sobrepostos. É esta a questão que o método de classificação do valor marginal aborda.

Método de classificação do valor marginal

Para resolver o problema de um número exponencialmente crescente de combinações que devem ser avaliadas, existe uma otimização que calcula o valor por produto partilhado de cada desconto no conjunto de produtos aos quais podem ser aplicados dois ou mais descontos. Referimo-nos a isto valor como o valor marginal do desconto para os produtos partilhados. O valor marginal é o aumento médio por produto do montante total do desconto quando os produtos partilhados são incluídos em cada desconto. O valor marginal é calculado tomando o montante total do desconto (D_Total), subtraindo o montante do desconto sem os produtos partilhados (D_{Menos Partilhado}) e dividindo essa diferença pelo número de produtos partilhados (Itens_Partilhado).

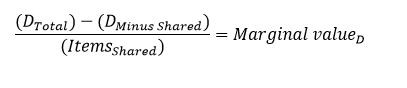
Após o cálculo do valor marginal de cada desconto num conjunto partilhado de produtos, os descontos são aplicados aos produtos partilhados por ordem, exaustivamente, do valor marginal mais elevado para o valor marginal mais baixo. Para isto método, todas as restantes possibilidades de desconto não são comparadas de cada vez que uma única instância de um desconto é aplicada. Em vez disso, os descontos sobrepostos são comparados uma vez e depois aplicados por ordem. Não são efectuadas comparações adicionais. O cálculo da classificação do valor marginal é automaticamente acionado quando o número total de combinações possíveis excede um limiar predefinido. O tempo aceitável para calcular o desconto total varia consoante o sector retalhista. No entanto, isto tempo situa-se geralmente no intervalo de dezenas de milissegundos a um segundo.