Splines Cardinais no GDI+
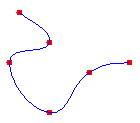
Um spline cardinal é uma sequência de curvas individuais unidas para formar uma curva maior. O spline é especificado por uma matriz de pontos e um parâmetro de tensão. Um spline cardinal passa suavemente pelos pontos na matriz. Não há cantos agudos nem mudanças abruptas na inclinação da curva. A ilustração a seguir mostra um conjunto de pontos e um spline cardinal que passa pelos pontos no conjunto.
Splines físicos e matemáticos
Um spline físico é uma peça fina de madeira ou outro material flexível. Antes do advento do splines matemáticos, os designers usavam splines físicos para desenhar curvas. O designer colocava o spline em um pedaço de papel e ancorava-o em um determinado conjunto de pontos. Então o designer podia criar uma curva desenhando ao longo do spline com uma caneta ou um lápis. Um determinado conjunto de pontos podia produzir uma variedade de curvas, dependendo das propriedades do spline físico. Por exemplo, um spline com uma alta resistência à curvatura geraria uma curva diferente daquela de um spline extremamente flexível.
As fórmulas para splines matemáticos são baseadas nas propriedades de barras flexíveis, portanto, as curvas produzidas por splines matemáticos são semelhantes às curvas antes produzidas por splines físicos. Assim como splines físicos de tensão diferente produzirão curvas diferentes em um determinado conjunto de pontos, splines matemáticos com valores diferentes para o parâmetro de tensão produzirão curvas diferentes em um determinado conjunto de pontos. A ilustração a seguir mostra quatro splines cardinais passando pelo mesmo conjunto de pontos. A tensão é mostrada para cada spline. Uma tensão de 0 corresponde à tensão física infinita, forçando a curva a seguir o caminho mais curto (linhas retas) entre os pontos. Uma tensão de 1 corresponde à ausência de tensão física, permitindo que o spline siga o caminho de menor curvatura total. Com valores de tensão superiores a 1, a curva comporta-se como uma mola comprimida, pressionada para seguir um caminho mais longo.
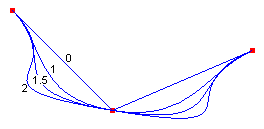
Os quatro splines na ilustração anterior compartilham a mesma linha tangente no ponto de partida. A tangente é a linha desenhada do ponto de partida até o próximo seguinte ao longo da curva. Da mesma forma, a tangente compartilhada no ponto final é a linha desenhada do ponto final até o ponto anterior na curva.
Para desenhar um spline cardinal, você precisa de uma instância da classe, um Pene uma matriz de objetos A instância da classe fornece o método, que desenha o DrawCurve spline, e os Pen atributos de Point armazenamento do spline, como largura e cor da GraphicsGraphics linha. A matriz de Point objetos armazena os pontos pelos quais a curva passará. O exemplo de código a seguir mostra como desenhar um spline cardinal que passa pelos pontos no myPointArray. O terceiro parâmetro é a tensão.
myGraphics.DrawCurve(myPen, myPointArray, 1.5f);
myGraphics.DrawCurve(myPen, myPointArray, 1.5F)
Confira também
.NET Desktop feedback
