Bézier Splines em GDI+
Uma spline de Bézier é uma curva especificada por quatro pontos: dois pontos finais (p1 e p2) e dois pontos de controlo (c1 e c2). A curva começa em p1 e termina em p2. A curva não passa pelos pontos de controle, mas os pontos de controle atuam como ímãs, puxando a curva em determinadas direções e influenciando a maneira como a curva se dobra. A ilustração a seguir mostra uma curva de Bézier juntamente com seus pontos finais e pontos de controle.
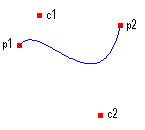
A curva começa em p1 e se move em direção ao ponto de controle c1. A linha tangente à curva em p1 é a linha traçada de p1 a c1. A linha tangente no ponto final p2 é a linha traçada de c2 a p2.
Desenho de Splines de Bézier
Para desenhar um spline de Bézier, você precisa de uma instância da classe Graphics e um Pen. A instância da classe Graphics fornece o método DrawBezier e o Pen armazena atributos, como largura e cor, da linha usada para renderizar a curva. O Pen é passado como um dos argumentos para o método DrawBezier. Os argumentos restantes passados para o método DrawBezier são os pontos de extremidade e os pontos de controle. O exemplo a seguir desenha uma spline de Bézier com ponto inicial (0, 0), pontos de controle (40, 20) e (80, 150) e ponto final (100, 10):
myGraphics.DrawBezier(myPen, 0, 0, 40, 20, 80, 150, 100, 10);
myGraphics.DrawBezier(myPen, 0, 0, 40, 20, 80, 150, 100, 10)
A ilustração a seguir mostra a curva, os pontos de controle e duas linhas tangentes.
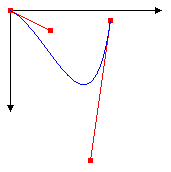
As estrias Bézier foram originalmente desenvolvidas por Pierre Bézier para design na indústria automóvel. Desde então, provaram ser úteis em muitos tipos de design assistido por computador e também são usados para definir os contornos das fontes. As estrias de Bézier podem produzir uma grande variedade de formas, algumas das quais são mostradas na ilustração a seguir.

Ver também
.NET Desktop feedback
