Azure Machine Learning の Jupyter Notebook 対応 ( 前編 )
Microsoft Japan Data Platform Tech Sales Team
森本 信次
Azure Machine Learning ( 以降 Azure ML )は Microsoft が提供しているクラウドベースの機械学習サービスです。Azure ML では ブラウザーを使って様々な機械学習の手法を実行することが可能ですが、Jupyter Notebook を使用することも可能となっています。
Jupyter Notebook とは、ノートブック形式で作成したプログラムを実行し、実行結果を保持しながら、データ分析作業を進めるためのツールです。プログラムとその実行結果やその際のメモを簡単に作成、確認することができるため、自分自身の過去の作業内容の振り返りや、チームメンバーへ作業結果を共有する際に便利なほか、スクール形式での授業や研修などでの利用にも向いています。
ではさっそく、Azure Machine Learning Studio で提供されている チュートリアルを実際に進めながら Notebook の使い勝手を見ていきたいと思いますが、必要に応じて以下 のMicrosoft アカウントの作成およびワークスペースの作成を行うようにしてください。
Microsoft アカウントの作成
Microsoft アカウントをもっていない場合にはリンク先から作成します。
ワークスペースの作成
下記リンクを開き「Get Started」ボタンをクリックし、Microsoft アカウントにサインインします。
Microsoft Azure Machine Learning Studio
成功していればワークスペースが作成されており以下のような画面が開きます。
Jupter Notebook の作成
画面左下の「+NEW」をクリックすると以下のような画面が開きます。 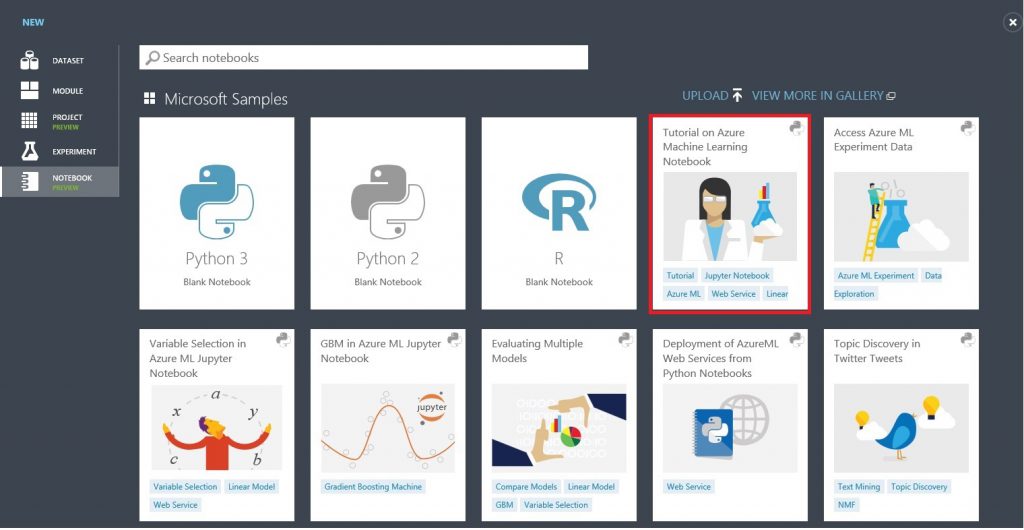
Notebook から Pythonの バージョンを選択し新しいNotebookを作成する事も可能ですが、今回はチュートリアル 「Tutorial on Azure Machine Learning Notebook 」を選択します。このチュートリアルでは統計学における回帰分析の一種である 線形回帰 ( linear regression ) を使い住宅価格の予測を行うシナリオとなっています。 
このように、すでにサンプルのコード ( Python ) および解説が含まれるている Notebook が開きます。
使用するデータ
このチュートリアルではボストンの住宅に関するデータセットを使用。データセットには 506 件のデータが含まれ、13種類の説明変数 ( 部屋の数、築年数、町の犯罪率 など ) があり、予測したい目的変数 を住宅の価格としています。 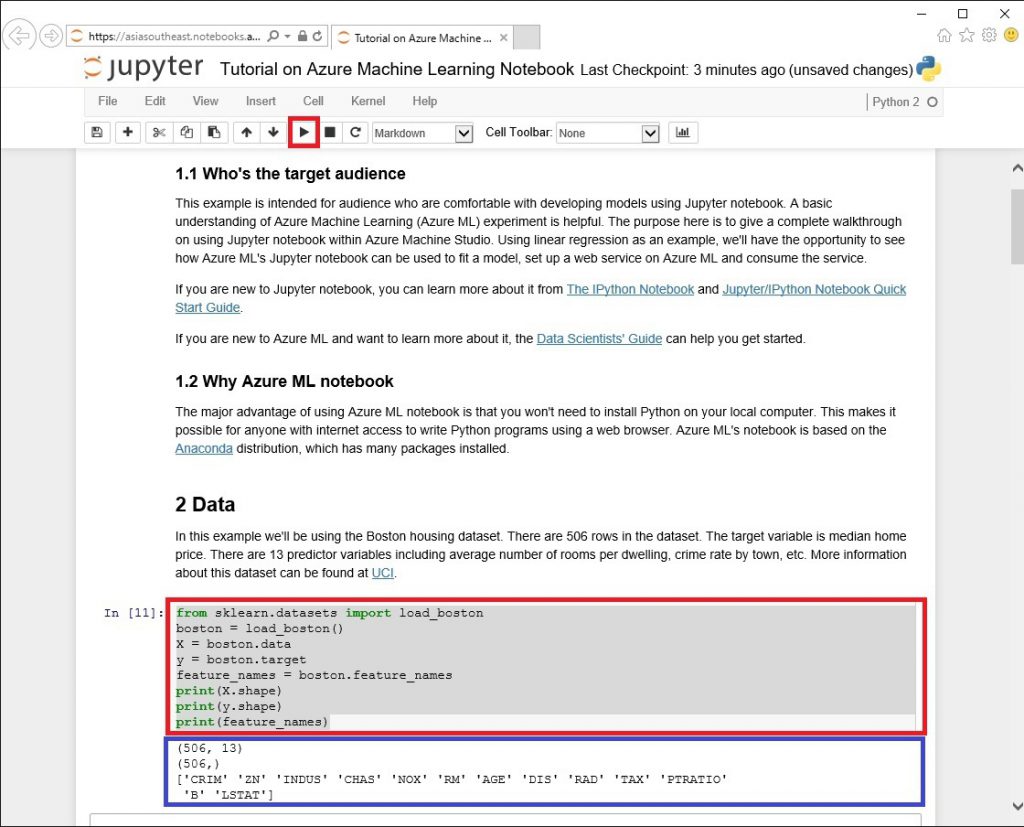
Notebook の使い方としては、対象の Python のコードを選択し ( 赤枠 )「➤」をクリックまたは Shift + Enter を実行すると、実行した結果が表示 ( 青枠 )されます。今回使用しているデータの解説はこちらをご覧ください。
Python の機械学習ライブラリ「sklearn」による線形回帰
それではさっそくこのデータを新しい変数 “mydata”に割り当てて、線形モデルの開発に使用することにします。実際のところフューチャー・エンジニアリングおよび変数の選択のために多くの時間を使いたいところですが、今回はすべての変数を使用してモデルにフィットさせるようにしたいと思います。
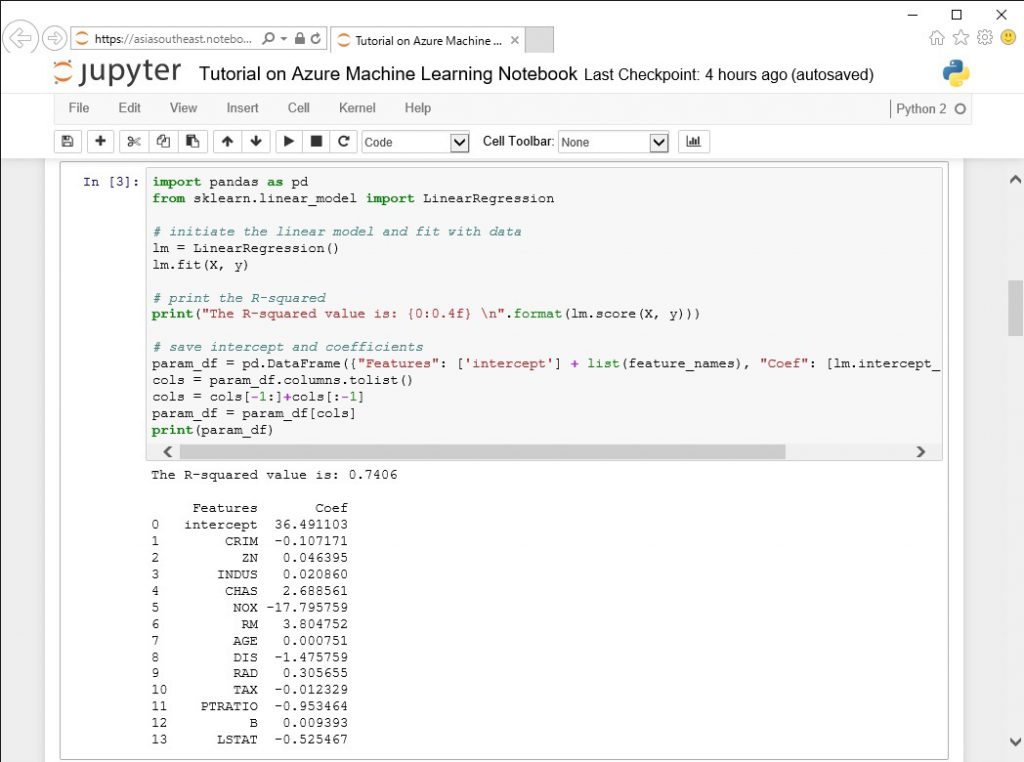
R-squared ( 決定係数 ) = 0.7406 という結果がでていますが、この R-squared は 目的変数が説明変数によってどれぐらい説明できるかを表す統計用語です、0から1までの値をとり、1に近いほどその説明変数で説明できるという意味になります。
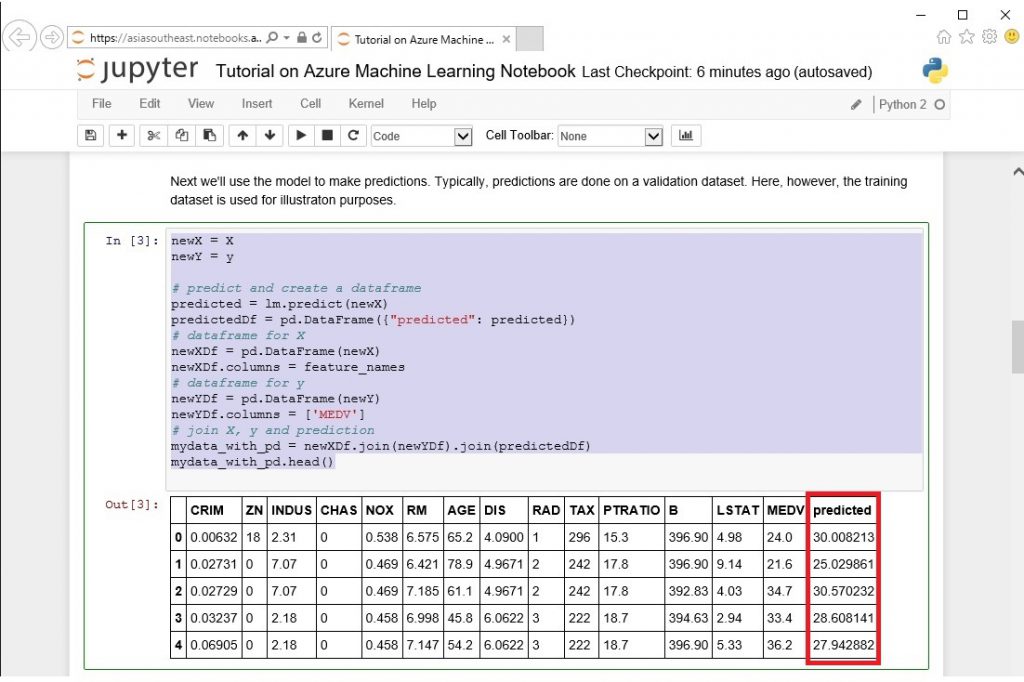
次に予測を行うためモデルを使ってみましょう、通常は適切なデータセットに基づいて予測を行うべきですが、今回はこのチュートリアルの解説を目的としているため、簡易的なデータセットを使用しています。
「predicted」 列が予測された値 ( 価格 )になります。
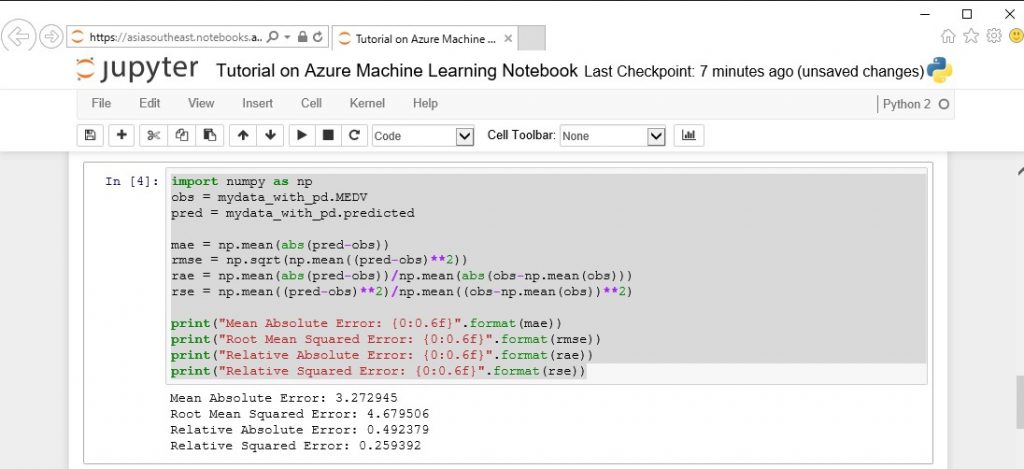
予測値に対する 以下の各統計値を計算してみましょう。
•平均絶対誤差(Mean Absolute Error)
* 絶対誤差の平均です (誤差とは、予測された値と実際の値との差です)。
•二乗平均平方根誤差(Root Mean Squared Error)
* テスト データセットに対して実行した予測の二乗誤差平均の平方根です。
•相対絶対誤差(Relative Absolute Error)
* 実際の値とすべての実際の値の平均との絶対差を基準にした絶対誤差の平均です。
•相対二乗誤差(Relative Squared Error)
* 実際の値とすべての実際の値の平均との二乗差を基準にした二乗誤差の平均です。
いかがでしたでしょうか ? ここまでで Jupyter Notebook を使用して 使用するデータの把握、予測モデルの作成、予測、統計量の確認の実施までの流れを見ていただきました。
次回 ( 後編 )では作成したモデルを Web サービスとしてデプロイし、プログラムコードから呼び出しができるところまでを解説したいと思います。