Aplicar transformações em Direct2D
Em Desenho com Direct2D, vimos que o método ID2D1RenderTarget::FillEllipse desenha uma elipse alinhada aos eixos x e y. Mas suponha que você queira desenhar uma elipse inclinada em um ângulo?

Usando transformações, você pode alterar uma forma das seguintes maneiras.
- Rotação em torno de um ponto.
- Dimensionamento.
- Tradução (deslocamento na direção X ou Y).
- Distorção (também conhecida como tesoura).
Uma transformação é uma operação matemática que mapeia um conjunto de pontos para um novo conjunto de pontos. Por exemplo, o diagrama a seguir mostra um triângulo girado ao redor do ponto P3. Depois que a rotação é aplicada, o ponto P1 é mapeado para P1', o ponto P2 é mapeado para P2' e o ponto P3 é mapeado para si mesmo.
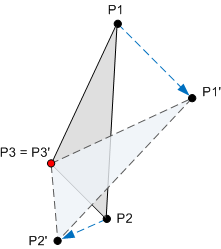
As transformações são implementadas usando matrizes. No entanto, você não precisa entender a matemática das matrizes para usá-las. Se você quiser saber mais sobre a matemática, confira Apêndice: Transformações de Matriz.
Para aplicar uma transformação em Direct2D, chame o método ID2D1RenderTarget::SetTransform. Esse método usa uma estrutura D2D1_MATRIX_3X2_F que define a transformação. Você pode inicializar essa estrutura chamando métodos na classe D2D1::Matrix3x2F . Essa classe contém métodos estáticos que retornam uma matriz para cada tipo de transformação:
Por exemplo, o código a seguir aplica uma rotação de 20 graus ao redor do ponto (100, 100).
pRenderTarget->SetTransform(
D2D1::Matrix3x2F::Rotation(20, D2D1::Point2F(100,100)));
A transformação é aplicada a todas as operações de desenho posteriores até que você chame SetTransform novamente. Para remover a transformação atual, chame SetTransform com a matriz de identidade. Para criar a matriz de identidade, chame a função Matrix3x2F::Identity .
pRenderTarget->SetTransform(D2D1::Matrix3x2F::Identity());
Desenhando mãos do relógio
Vamos colocar transformações a serem usadas convertendo nosso programa Circle em um relógio analógico. Podemos fazer isso adicionando linhas para as mãos.
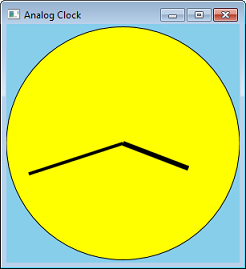
Em vez de calcular as coordenadas das linhas, podemos calcular o ângulo e aplicar uma transformação de rotação. O código a seguir mostra uma função que desenha uma mão de relógio. O parâmetro fAngle fornece o ângulo da mão, em graus.
void Scene::DrawClockHand(float fHandLength, float fAngle, float fStrokeWidth)
{
m_pRenderTarget->SetTransform(
D2D1::Matrix3x2F::Rotation(fAngle, m_ellipse.point)
);
// endPoint defines one end of the hand.
D2D_POINT_2F endPoint = D2D1::Point2F(
m_ellipse.point.x,
m_ellipse.point.y - (m_ellipse.radiusY * fHandLength)
);
// Draw a line from the center of the ellipse to endPoint.
m_pRenderTarget->DrawLine(
m_ellipse.point, endPoint, m_pStroke, fStrokeWidth);
}
Esse código desenha uma linha vertical, começando do centro da face do relógio e terminando no ponto de extremidadePoint. A linha é girada ao redor do centro da elipse aplicando uma transformação de rotação. O ponto central da rotação é o centro da elipse que forma a face do relógio.
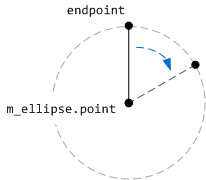
O código a seguir mostra como toda a face do relógio é desenhada.
void Scene::RenderScene()
{
m_pRenderTarget->Clear(D2D1::ColorF(D2D1::ColorF::SkyBlue));
m_pRenderTarget->FillEllipse(m_ellipse, m_pFill);
m_pRenderTarget->DrawEllipse(m_ellipse, m_pStroke);
// Draw hands
SYSTEMTIME time;
GetLocalTime(&time);
// 60 minutes = 30 degrees, 1 minute = 0.5 degree
const float fHourAngle = (360.0f / 12) * (time.wHour) + (time.wMinute * 0.5f);
const float fMinuteAngle =(360.0f / 60) * (time.wMinute);
DrawClockHand(0.6f, fHourAngle, 6);
DrawClockHand(0.85f, fMinuteAngle, 4);
// Restore the identity transformation.
m_pRenderTarget->SetTransform( D2D1::Matrix3x2F::Identity() );
}
Você pode baixar o projeto completo do Visual Studio Direct2D Exemplo de Relógio. (Só por diversão, a versão de download adiciona um gradiente radial à face do relógio.)
Combinando transformações
As quatro transformações básicas podem ser combinadas multiplicando duas ou mais matrizes. Por exemplo, o código a seguir combina uma rotação com uma tradução.
const D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(20);
const D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(40, 10);
pRenderTarget->SetTransform(rot * trans);
A classe Matrix3x2F fornece operator*() para multiplicação de matriz. A ordem na qual você multiplica as matrizes é importante. Definir uma transformação (M × N) significa "Aplicar M primeiro, seguido por N". Por exemplo, aqui está a rotação seguida pela tradução:
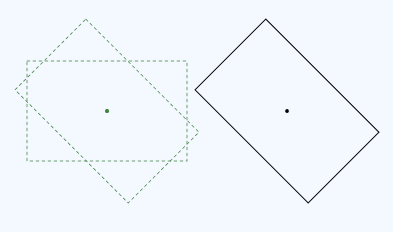
Este é o código para esta transformação:
const D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(45, center);
const D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(x, 0);
pRenderTarget->SetTransform(rot * trans);
Agora compare essa transformação com uma transformação na ordem inversa, tradução seguida de rotação.
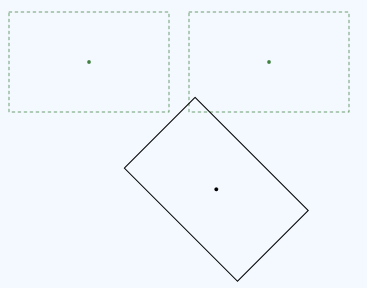
A rotação é executada ao redor do centro do retângulo original. Este é o código para essa transformação.
D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(45, center);
D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(x, 0);
pRenderTarget->SetTransform(trans * rot);
Como você pode ver, as matrizes são as mesmas, mas a ordem das operações foi alterada. Isso acontece porque a multiplicação de matriz não é comutativa: M × N ≠ N × M.