Curvas

Uma curva regular é um conjunto de pixels realçados em uma exibição de raster (ou pontos em uma página impressa) que definem o perímetro (ou parte do perímetro) de uma seção conic. Uma curva irregular é um conjunto de pixels que define uma curva que não se encaixa no perímetro de uma seção conic. O ponto final é excluído de uma curva, assim como é excluído de uma linha.

Quando um aplicativo chama uma das funções de desenho de curva, o GDI divide a curva em vários segmentos de linha extremamente pequenos e discretos. Depois de determinar os pontos de extremidade (ponto inicial e ponto final) para cada um desses segmentos de linha, a GDI determina quais pixels (ou pontos) definem cada linha aplicando seu DDA.

Um aplicativo pode desenhar uma elipse ou parte de uma elipse chamando a função Arc . Essa função desenha a curva dentro do perímetro de um retângulo invisível chamado retângulo delimitador. O tamanho da elipse é especificado por dois radiais invisíveis que se estendem do centro do retângulo até os lados do retângulo. A ilustração a seguir mostra um arco (parte de uma elipse) desenhado usando a função Arc .

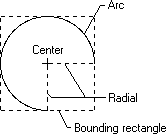
Ao chamar a função Arc , um aplicativo especifica as coordenadas do retângulo delimitador e radiais. A ilustração anterior mostra o retângulo e radiais com linhas tracejadas enquanto o arco real foi desenhado usando uma linha sólida.

Ao desenhar o arco de outro objeto, o aplicativo pode chamar as funções SetArcDirection e GetArcDirection para controlar a direção (no sentido horário ou no sentido anti-horário) em que o objeto é desenhado. A direção padrão para arcos de desenho e outros objetos é no sentido anti-horário.

Além de desenhar reticências ou partes de reticências, os aplicativos podem desenhar curvas irregulares chamadas curvas Bézier. Uma curva Bézier é uma curva irregular cuja curvatura é definida por quatro pontos de controle (p1, p2, p3 e p4). Os pontos de controle p1 e p4 definem os pontos inicial e final da curva e os pontos de controle p2 e p3 definem a forma da curva marcando pontos em que a curva inverte a orientação, conforme mostrado no diagrama a seguir.

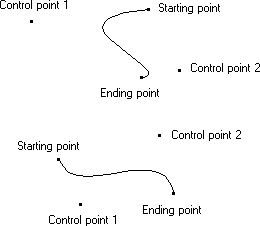
Um aplicativo pode desenhar curvas irregulares chamando a função PolyBezier , fornecendo os pontos de controle apropriados.