Desequilíbrios de dados
Quando os rótulos de dados têm mais de uma categoria do que de outra, dizemos que há um desequilíbrio de dados. Por exemplo, lembre-se de que, em nosso cenário, estamos tentando identificar os objetos encontrados por sensores de drones. Os dados estão desequilibrados, porque há um número muito diferente de alpinistas, animais, árvores e pedras nos dados de treinamento. Podemos ver isso tabulando esses dados:
| Rótulo | Hiker | Animal | Árvore | Pedra |
|---|---|---|---|---|
| Contagem | 400 | 200 | 800 | 800 |
Ou plotando:
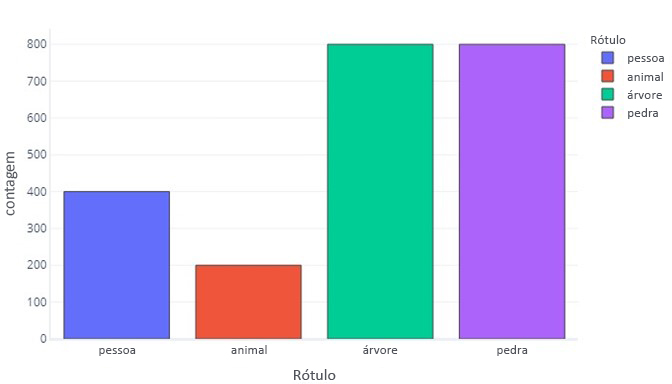
Observe como a maioria dos dados são trees ou rocks. Um conjuntos de dados balanceado não tem esse problema.
Por exemplo, se tentarmos prever se um objeto é um alpinista, um animal, uma árvore ou uma rocha, o ideal será ter um número igual de todas as categorias, da seguinte forma:
| Rótulo | Hiker | Animal | Árvore | Pedra |
|---|---|---|---|---|
| Contagem | 550 | 550 | 550 | 550 |
Se simplesmente tentarmos prever se um objeto é um alpinista, o ideal será ter um número igual de objetos alpinista e não alpinista:
| Rótulo | Hiker | Non-Hiker |
|---|---|---|
| Contagem | 1100 | 1100 |
Por que os desequilíbrios de dados são importantes?
Os desequilíbrios de dados são importantes porque os modelos podem aprender a imitar esses desequilíbrios quando não forem desejáveis. Por exemplo, vamos fingir que treinamos um modelo de regressão logística para identificar objetos como hiker ou not-hiker. Se os dados de treinamento forem altamente dominados por rótulos "alpinista", o treinamento desviará o modelo para quase sempre retornar rótulos "alpinista". No entanto, no mundo real, podemos descobrir que a maioria das coisas que os drones encontram são árvores. O modelo polarizado provavelmente rotularia muitas dessas árvores como trilheiros.
Esse fenômeno ocorre porque as funções de custo, por padrão, determinam se a resposta correta foi dada. Isso significa que, para um conjuntos de dados polarizado, a maneira mais simples para um modelo alcançar o desempenho ideal pode ser ignorar os recursos fornecidos e sempre, ou quase sempre, retornar a mesma resposta. Isso pode ter consequências devastadoras. Por exemplo, imagine que nosso modelo de alpinista/não alpinista seja treinado em dados nos quais apenas uma de cada mil amostras contenha um alpinista. Um modelo que aprendeu a sempre retornar "não alpinista" tem uma precisão de 99,9%. Essa estatística parece excelente, mas o modelo é inútil porque ele nunca nos dirá se alguém está na montanha, e não vamos salvá-lo em caso de avalanche.
Desvio em uma matriz de confusão
Matrizes de confusão são a chave para identificar desequilíbrios de dados ou desvios de modelo. Em um cenário ideal, os dados de teste têm um número aproximadamente uniforme de rótulos, e as previsões feitas pelo modelo também são distribuídas aproximadamente entre os rótulos. Para 1.000 exemplos, um modelo imparcial, mas que geralmente obtém respostas erradas, pode ter a seguinte aparência:
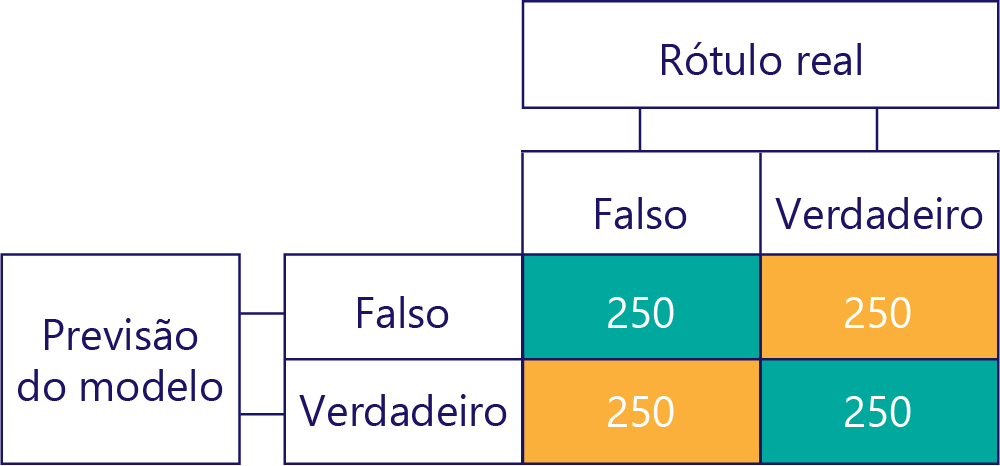
Podemos dizer que os dados de entrada são imparciais, pois as somas das linhas são as mesmas (500 cada), indicando que metade dos rótulos é "true" e a outra metade é "false". Da mesma forma, podemos ver que o modelo está dando respostas imparciais, porque ele está retornando true na metade do tempo e false na outra metade do tempo.
Por outro lado, os dados polarizados contêm principalmente um tipo de rótulo, da seguinte forma:
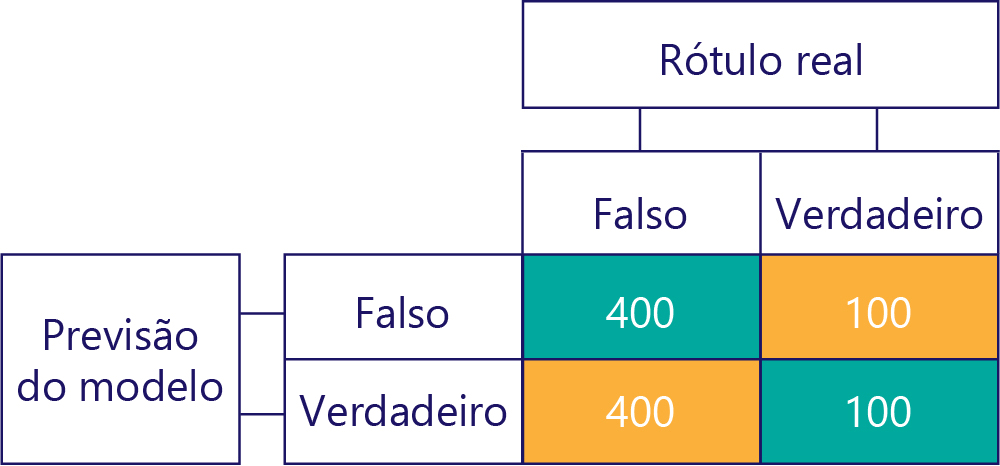
Da mesma forma, um modelo polarizado produz principalmente um tipo de rótulo, da seguinte forma:
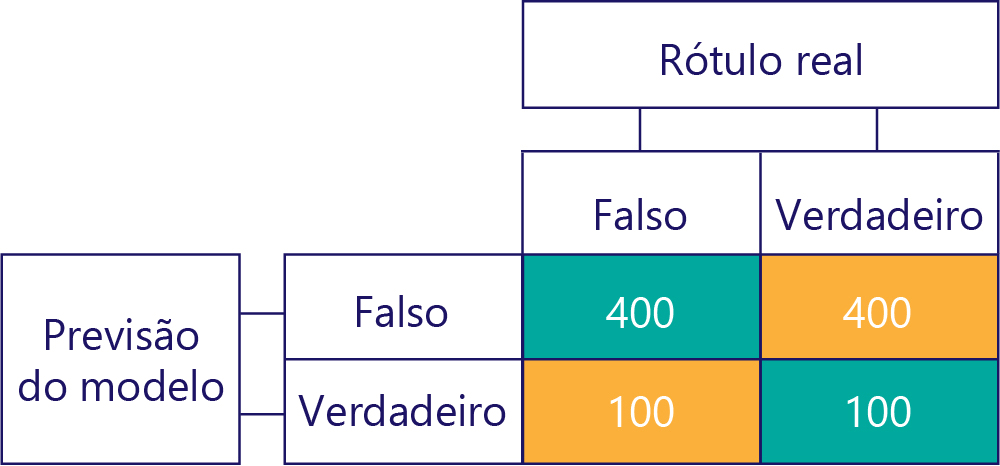
Desvio de modelo não é precisão
Lembre-se que desvio não é precisão. Por exemplo, alguns dos exemplos anteriores são tendenciosos e outros não, mas todos mostram um modelo que obtém a resposta correta 50% do tempo. Como um exemplo mais extremo, a matriz abaixo mostra um modelo imparcial que é impreciso:
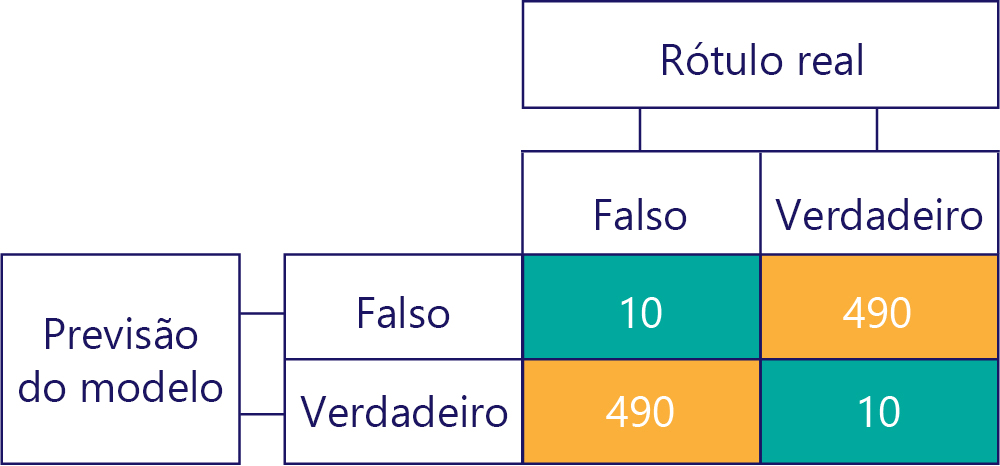
Observe como a soma do número de linhas e colunas resulta em 500, indicando que ambos os dados são balanceados e o modelo não é polarizado. No entanto, esse modelo está recebendo quase todas as respostas incorretas!
É claro que nossa meta é que os modelos sejam precisos e imparciais, como:
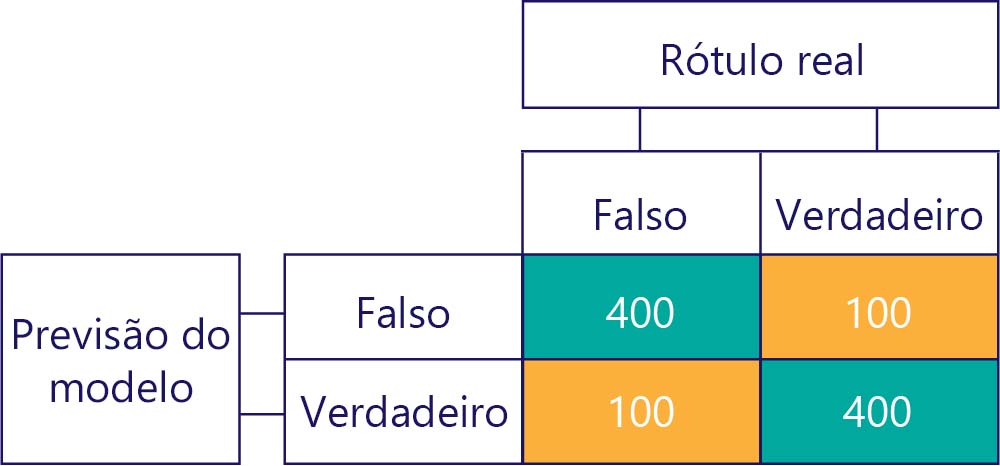
... mas precisamos garantir que nossos modelos precisos não sejam polarizados pelo simples fato dos dados serem:
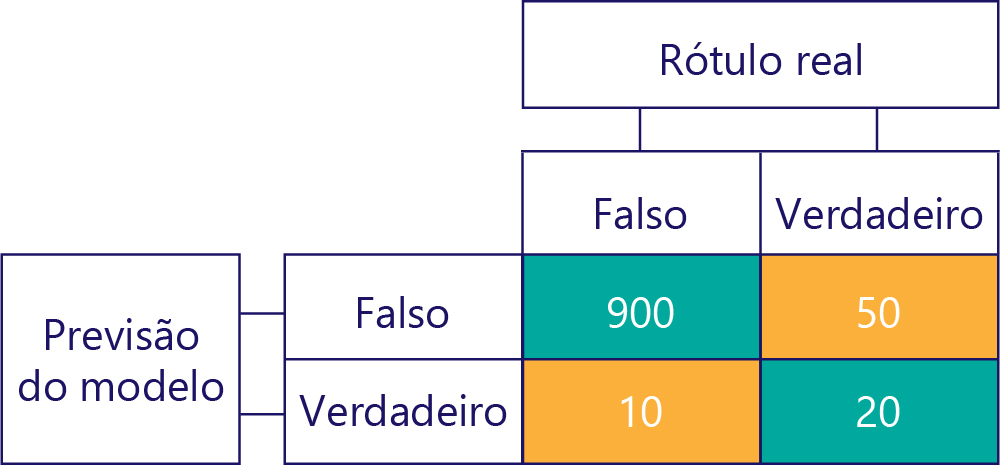
Neste exemplo, observe como os rótulos reais são predominantemente false (coluna esquerda, mostrando um desequilíbrio de dados) e o modelo também retorna false frequentemente (linha superior, mostrando desvio de modelo). Esse modelo não é bom para dar respostas 'True' corretamente.
Evitando as consequências de dados desequilibrados
Algumas das maneiras mais simples de evitar as consequências de dados desequilibrados são:
- Evite-os selecionando melhor os dados.
- Crie uma "nova amostra" dos seus dados para que eles contenham duplicatas da classe de rótulo minoritária.
- Faça alterações na função de custo para que ela priorize rótulos menos comuns. Por exemplo, se a resposta errada dada for Árvore, a função de custo poderá retornar 1. No entanto, se a resposta errada dada for Alpinista, ela poderá retornar 10.
Exploraremos esses métodos no exercício a seguir.